Games and Mathematics (12 page)
Read Games and Mathematics Online
Authors: David Wells

Part II
Mathematics: game-like, scientific and perceptual
Mathematics: game-like, scientific and perceptual
Introduction
These three aspects
of mathematics could be presented in any order. Which is the best order? Professional mathematical papers are frequently criticised for only presenting the game-like aspects of mathematics while saying nothing about scientific or perceptual aspects, as well as omitting every sign of how their results were discovered in the first place. Very occasional exceptions, such as Euler, are famous for being exceptional. Henri Poincaré asked:
of mathematics could be presented in any order. Which is the best order? Professional mathematical papers are frequently criticised for only presenting the game-like aspects of mathematics while saying nothing about scientific or perceptual aspects, as well as omitting every sign of how their results were discovered in the first place. Very occasional exceptions, such as Euler, are famous for being exceptional. Henri Poincaré asked:
Will we ever be able to say that we understand a theory if we want to give to it straight away its final form, that impeccable logic imposes on it? Which ideas were tried out and discarded, which ideas were tried out and retained? If we don't know these things we will not really understand it, we will even not be able to remember it; at best we will only remember it by learning it off by heart.[Poincaré 1899]
‘Ideas were tried out and discarded…ideas were tried out and retained?’ Yes, indeed! The process of trying out ideas, of experimenting with this approach then that approach, of abandoning ideas that don't work, is a process of play, of experiment, of conjecturing, testing, and then, very likely, rejecting: ‘Aha! Of course, it's an analogue of the Laplace transform, let's see [CHECKS BY CALCULATION]. Oh, it isn't. What a pity! Back to the drawing board!’
This is a scientific process, quite different from the textbook approach which tells you to identify the problem by TYPE, select the recommended METHOD, insert the specific DETAILS of your problem, and SWITCH THE METHOD ON! Gottlob Frege, who was a mathematician as well as a logician and philosopher, wrote that,
The aim of proof is…not merely to place the truth of a proposition beyond all doubt, but also to afford us insight into the dependence of truths upon one another.[Frege 1884/1953: 2
e
]
The explanations in mathematicians’ published papers may be logically convincing yet unconvincing in every other respect which makes them much harder to read and understand. As Hermann Weyl wrote:
We are not very pleased when we are forced to accept a mathematical truth by virtue of a complicated chain of formal conclusions and computations,
which we traverse blindly
, link by link, feeling our way by touch.
We want first an overview
of the aim and of the road; we want to understand the
idea
of the proof, the deeper context.
The italics are ours. The emphasis on perception could not be clearer. ‘Aha! Now I see it!’ is the hope and expectation of all mathematicians (and the despair of many school pupils.) To play around with a problem, to ‘suck it and see’, to turn it over and look at it from another perspective, is the very essence of mathematics. It is no coincidence, of course, that
playing
is just what game players do.
playing
is just what game players do.
The three aspects cannot be separated. There are few examples of purely perceptual maths and none at all if you argue that perception in mathematics is always game-like because the ideas are already abstract. Nor can mathematics be purely scientific: it must in the final analysis be game-like. That is one of the differences between maths and physics, or chemistry. Experiment may convince a mathematician
psychologically
that a result must be correct but he or she still wants a proof, not just because proofs are convincing but because the effort of creating a proof for a challenging solution
creates new ideas
that illuminate the problem left behind and the path ahead as the sun rises on yet another region of the endless mathematical landscape that mathematical gold diggers rush to explore.
psychologically
that a result must be correct but he or she still wants a proof, not just because proofs are convincing but because the effort of creating a proof for a challenging solution
creates new ideas
that illuminate the problem left behind and the path ahead as the sun rises on yet another region of the endless mathematical landscape that mathematical gold diggers rush to explore.
We shall start with game-like mathematics, then turn to the scientific aspect, and then finally to the foundation of all art and science – and mathematics – perception.
For the reasons already given, the distribution of topics between the following chapters is rather arbitrary. With a slight change in perspective or a different emphasis, an illustrative example in one chapter could readily be moved to another.
6
Game-like mathematics
Introduction
Tactics and strategy

Sums of cubes and a hidden connection
Game-like mathematics
Game-like mathematics is a world of brilliant moves and cunning tactics, subtle and deep strategy, beautiful combinations and transformations, profound intuitions, and
proof
.
proof
.
We first glance at the abacus and Cuisenaire rods, and examples of game-like tactics and strategy in ordinary arithmetic. Even small children can use tricks and short cuts to solve arithmetical problems more easily. These are their introduction to game-like tactics and stratagems and to the importance of
not
simply relying on routine algorithms – let alone on calculators!
not
simply relying on routine algorithms – let alone on calculators!
Hidden connections in algebra is a fascinating theme: repeatedly, patterns and analogies turn up which seem to have a deeper significance. Usually they do, but how to find it? Geometrical figures always mean something but algebraic expressions or equations often seem to mean little – but then some neat move or an elegant transformation or a simplification is made, and pattern and structure and
meaning
appear, almost as if by magic.
meaning
appear, almost as if by magic.
Jean le Rond d’Alembert (1717–1783) said that, ‘Algebra is generous. She often gives more than is asked for’ [Boyer
1991
: 439] but only to those who learn to play the game of algebra fluently and with insight and imagination. Later we shall see how what appears to be a mere coincidence is connected to a surprising theorem by Liouville. This will be followed by a masterpiece by the incomparable Euler, that has also been analysed by George Polya. Polya claimed that it was all about scientific induction but we think it is at least as much about game-like brilliance.
1991
: 439] but only to those who learn to play the game of algebra fluently and with insight and imagination. Later we shall see how what appears to be a mere coincidence is connected to a surprising theorem by Liouville. This will be followed by a masterpiece by the incomparable Euler, that has also been analysed by George Polya. Polya claimed that it was all about scientific induction but we think it is at least as much about game-like brilliance.
In
Chapter 7
we turn to geometry and Euclid
, for two thousand years the paradigm of game-like mathematics – which isn't to say that much of geometry hasn't first been discovered by experiment or that geometers haven't made mistakes. They have, but relatively few and geometry is far more notable for
its wealth of surprises, the sheer elegance of its arguments and the depth of its insights.
Chapter 7
we turn to geometry and Euclid
, for two thousand years the paradigm of game-like mathematics – which isn't to say that much of geometry hasn't first been discovered by experiment or that geometers haven't made mistakes. They have, but relatively few and geometry is far more notable for
its wealth of surprises, the sheer elegance of its arguments and the depth of its insights.
Goodstein's analogiesR. L. Goodstein was a rare mathematician who took the analogies between mathematics and abstract games seriously. In his,
Recursive Number Theory
, he discussed ‘Arithmetic and the Game of Chess’:To the numerals correspond the chess pieces, and to the operations of arithmetic, the moves of the game. But the parallel is even closer than this, for to the problem of defining number corresponds the problem of defining the entities of the game…and a little later he added, as an aside, ‘Here at last we find the answer to the problem of the nature of numbers…’ [Goodstein
1957
].In his
Essays on the philosophy of mathematics
, he went further: ‘[mathematics] is the continual creation of new games and the comparative anatomy of games’ which shows much more insight. Even when he writes ‘If mathematics had no applications then it would indeed be “merely a game”’, he half-rescues himself by continuing, ‘Even so, not a meaningless game, for operating with symbols in a coherent structure is itself meaningful’ [Goodstein
1965
: 216, 111–112].In
Axiomatic Projective Geometry
, written with E. J. F. Primrose, Chapter X is titled ‘Geometry as a Board Game’, and justifies its title literally: ‘The game is played by placing rows of letters…in columns on a “board”. Each column serves to express an attribute of the geometry…’ and so on [Goodstein
1953
].In an earlier paper,
Geometry in Modern Dress
, Goodstein had taken the axioms of projective geometry and presented them lightheartedly, first in terms of typists and the typewriters they used at the International Typewriting Agency, and then in terms of the Game of Letter-Board
[Goodstein
1938
: 217].
The abacus is one of the oldest calculating devices, whether using a board with pebbles or beads strung on wires or sliding in slots. A few fortunate Romans even used a hand-held abacus, made of a sheet with beads moving in parallel grooves. There is an example in the British Museum.
Mostly, the Romans used loose stones, or
calculi
(whence our words to calculate, and calculus) on a ruled board or cloth so it is no surprise that they also referred to
ludus calculorum
, meaning any game using the same equipment.
calculi
(whence our words to calculate, and calculus) on a ruled board or cloth so it is no surprise that they also referred to
ludus calculorum
, meaning any game using the same equipment.
Addition on an abacus, or
soroban
, is like playing a simple board game, because you are physically moving pieces to achieve a desired result according to the rules. We might say that this is an
empirical
kind of arithmetic. Since an abacus expert hardly needs to think while using the device, experts can be extremely fast. In a contest in Tokyo in 1946, Kiyoshi Matsuzaki using a soroban easily defeated Private Thomas Wood using a hand-held electric calculator on addition, subtraction, multiplication and division problems [Tani
1964
: 7].
soroban
, is like playing a simple board game, because you are physically moving pieces to achieve a desired result according to the rules. We might say that this is an
empirical
kind of arithmetic. Since an abacus expert hardly needs to think while using the device, experts can be extremely fast. In a contest in Tokyo in 1946, Kiyoshi Matsuzaki using a soroban easily defeated Private Thomas Wood using a hand-held electric calculator on addition, subtraction, multiplication and division problems [Tani
1964
: 7].
Small children who use Cuisenaire rods to do sums are also playing a game with simple rules – and whatever method you use, these games have tactics and strategies. What is 8 × 35? Well, 8 is 2 × 2 × 2, so to multiply by 8 we double three times: 35 – 70 – 140 – 280, the correct answer, easily calculated mentally.
What is 12 × 35? Since 12 = 8 + 4, the answer from the previous calculation is 280 + 140 = 420. However, you could also notice that 12 = 3 × 2 × 2 and 3 × 35 = 105, so doubling twice we get, 105 − 210 − 420.
As a last resort, you could use your 12 times table: 12 × 30 = 360 and 12 × 5 = 60, making a total of 420. In this case recalling your tables is just as quick as the other routes, provided that you
don't
try to visualise a standard sum in your head, complete with ‘write down 0 and carry 6’.
don't
try to visualise a standard sum in your head, complete with ‘write down 0 and carry 6’.
These are examples of very basic tactics and strategy. The strategy is to look at the particular features of the numbers you are multiplying by, the tactics actually carry out the strategy. The same approach is vitally important in programming computers. By exploiting specific features of the problem at hand, you can often program it more simply.
There are many other tactics-and-strategies that well-taught children master. Thus any sharp-eyed observer might notice that 9 × 11 = 99 which is 1 less than 10 × 10: similarly 7 × 9 = 63 and 8 × 8 = 64. So what is 15 × 17?
Here is the extended pattern. It
seems
that if you know your squares, for example that 15 squared is 225, then you can work out the products of numbers on either side of 15, by simply subtracting a smaller square. 15
2
= 225, so 14 × 16 = 224 and 13 × 17 = 221 and so on. But why should this work? To just spot the pattern and use it is to do science. How can we prove that the pattern is sound?
By this tactical sequence of moves:
 This pattern works for any starting square, and any pair on either side, so we could represent it (more briefly) in algebra like this:
This pattern works for any starting square, and any pair on either side, so we could represent it (more briefly) in algebra like this:
 For small children, and many adults, a geometric picture is more likely to be convincing (
For small children, and many adults, a geometric picture is more likely to be convincing (
Figure 6.1
). The 6 by 6 square and the 5 by 7 rectangle overlap. Comparing the row of 6 small squares along the top with the 5 small squares down the right-hand edge, shows that the large square is 1 small square bigger.
16 × 16 | 15 × 17 | 14 × 18 | 13 × 19 | 12 × 20 | 11 × 21 |
256 | 255 | 252 | 247 | 240 | 231 |
256–0 | 256–1 | 256–4 | 256–9 | 256–16 | 256–25 |
seems
that if you know your squares, for example that 15 squared is 225, then you can work out the products of numbers on either side of 15, by simply subtracting a smaller square. 15
2
= 225, so 14 × 16 = 224 and 13 × 17 = 221 and so on. But why should this work? To just spot the pattern and use it is to do science. How can we prove that the pattern is sound?
By this tactical sequence of moves:


Figure 6.1
). The 6 by 6 square and the 5 by 7 rectangle overlap. Comparing the row of 6 small squares along the top with the 5 small squares down the right-hand edge, shows that the large square is 1 small square bigger.
Figure 6.1
Illustration of (A − 1)(A + 1)
Illustration of (A − 1)(A + 1)

By exploiting tactics and strategy we can do many calculations more quickly and more enjoyably. For other calculations, however, the Four Rules are next best (after a calculator) though they are no more than clever algorithms. Using them is a pretty routine activity, and frankly – for the mathematician – disappointing and unproductive. Indeed, if the Four Rules were all you could use the counting numbers for, mathematics would never have taken off. Fortunately, just as we can see chess as either an abstract model of a real battle between blood-and-guts armies or an abstract game valued for itself, so we can turn aside from mundane arithmetic and consider the counting numbers purely for their own sake – which is just what the Greeks started to do, 2500 years ago. One tool for doing so is algebra.
On page 132 we shall sum the odd squares scientifically, by spotting a pattern. If we do the same for the sum of the cubes, our pattern spotting should lead to this result:
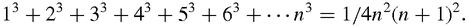 This is a neat result, and also surprising, because the right-hand side is the square of
This is a neat result, and also surprising, because the right-hand side is the square of
 n
n
(
n
+ 1) which is the sum of the counting numbers, so,
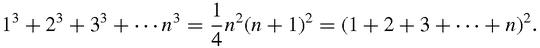 Is this a coincidence or is it deep? Is it a
Is this a coincidence or is it deep? Is it a
special
and isolated result or part of a
general
pattern? We haven't yet defined what we mean by a ‘coincidence’ in mathematics or what we mean by ‘deep’, so let's just say that if a result is connected to many other results (like Pythagoras’ theorem
) then it is deep, but if it is an isolated and unconnected result, then it is coincidental. That definition raises the question,
are there
any coincidental results in mathematics or must everything be connected to something else? Let's do a test, by looking at a neat property of the
divisor function
. This is denoted by d(
n
) and is equal to the number of divisors of the integer
n
. The divisors of 24 are,
That's 8 divisors in total, though we might have our doubts about 24 and 1. When counting the prime numbers we excluded 1. Should we count 1 here? 24 is, of course, a factor of itself but it is not a
proper
factor. Should be include 24?
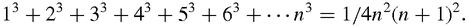
 n
n(
n
+ 1) which is the sum of the counting numbers, so,
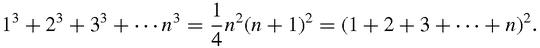
special
and isolated result or part of a
general
pattern? We haven't yet defined what we mean by a ‘coincidence’ in mathematics or what we mean by ‘deep’, so let's just say that if a result is connected to many other results (like Pythagoras’ theorem
) then it is deep, but if it is an isolated and unconnected result, then it is coincidental. That definition raises the question,
are there
any coincidental results in mathematics or must everything be connected to something else? Let's do a test, by looking at a neat property of the
divisor function
. This is denoted by d(
n
) and is equal to the number of divisors of the integer
n
. The divisors of 24 are,
24 | 12 | 8 | 6 | 4 | 3 | 2 | 1 |
proper
factor. Should be include 24?
The answer is subtle and illustrates how mathematicians decide on the details of many definitions. It turns out that if 24 and 1 are included, then the function d(
n
) has the very simple property that if
n
and
m
have no common factor apart from 1, then,
 A function with such a simple property is not only much easier to handle than a function lacking it, but the added simplicity is a strong hint that we are ‘on to something’. Therefore,
A function with such a simple property is not only much easier to handle than a function lacking it, but the added simplicity is a strong hint that we are ‘on to something’. Therefore,
a deliberate choice
was made, long ago, to include 1 and the number itself. Thus the factors of 15 and 28 are:
and the factors of 15×28 = 420 can be displayed in this table, which has 4×6 = 24 entries:
So d(15×28) = d(15)×d(28), but this would not be so if we excluded 420 and 1 from the divisors of 420, (and also we could not display the results in this simple table if 15 and 28 had any common factor, apart from 1).
n
) has the very simple property that if
n
and
m
have no common factor apart from 1, then,

a deliberate choice
was made, long ago, to include 1 and the number itself. Thus the factors of 15 and 28 are:
15: | 15 | 5 | 3 | 1 | d(15) = 4 | ||
28: | 28 | 14 | 7 | 4 | 2 | 1 | d(28) = 6 |
28 | 14 | 7 | 4 | 2 | 1 | |
15 | 420 | 210 | 105 | 60 | 30 | 15 |
5 | 140 | 70 | 35 | 20 | 10 | 5 |
3 | 84 | 42 | 21 | 12 | 6 | 3 |
1 | 28 | 14 | 7 | 4 | 2 | 1 |
Now for a theorem proved by Joseph Liouville (1809–1882). First we take any integer, 15 will do, and write down all its factors, and then underneath we write d(n) for each:
Liouville's theorem now says that,
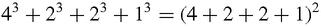 which is true. Similarly for 28:
which is true. Similarly for 28:
and,
 This is a weird theorem. What has it to do with the sum of consecutive cubes? The connection lies in the powers of primes, such as 2
This is a weird theorem. What has it to do with the sum of consecutive cubes? The connection lies in the powers of primes, such as 2
8
= 256.
15 | 5 | 3 | 1 | |
d( n ) | 4 | 2 | 2 | 1 |
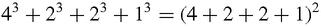
28 | 14 | 7 | 4 | 2 | 1 | |
d( n ) | 6 | 4 | 2 | 3 | 2 | 1 |

8
= 256.
If we write down its factors and their d(n) values we get:
and Liouville's theorem says that,
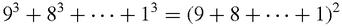 which is just the ‘coincidental’ property that we started with. It looks as if Liouville's theorem is a generalisation of our original result about sums of
which is just the ‘coincidental’ property that we started with. It looks as if Liouville's theorem is a generalisation of our original result about sums of
cubes and so our original ‘coincidence’ does seem to be a piece of a larger pattern [Dickson
1971
: v.1 286].
256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
d( n ) | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
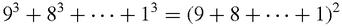
cubes and so our original ‘coincidence’ does seem to be a piece of a larger pattern [Dickson
1971
: v.1 286].
Liouville's theorem also suggests (naturally) some further questions.
If we take a handful of small numbers then we find that the left-hand side of our equation is less than the right-hand side:
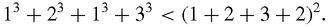 But with larger numbers, the LH side is larger:
But with larger numbers, the LH side is larger:

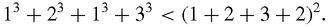

Other books
Skinner's Box (Fang Mu (Eastern Crimes)) by Lei Mi
Thursdays At Eight by Debbie Macomber
The Wake (And What Jeremiah Did Next) by Colm Herron
Folk Lore by Ellis, Joanne
Double The Risk by Samantha Cayto
Julia Gets a Life by Lynne Barrett-Lee
The Black Wolf's Mark by Pet TorreS
Dying Echo: A Grim Reaper Mystery (Grim Reaper Series) by Clemens, Judy
Penalty Shot by Matt Christopher
Gabby Revealed (Finding Perfect) by Gregory, Amy
