Games and Mathematics (11 page)
Read Games and Mathematics Online
Authors: David Wells

Near the boundary






We can see a simple example of this cross-over, from being calculated mathematically to being checked as if by a games player, by looking at a simple mathematical puzzle (
Figures 5.2
and
5.3
).
Figures 5.2
and
5.3
).
Figure 5.2
Chessboard with squares marked
Chessboard with squares marked

Figure 5.3
Chessboard with squares marked
Chessboard with squares marked

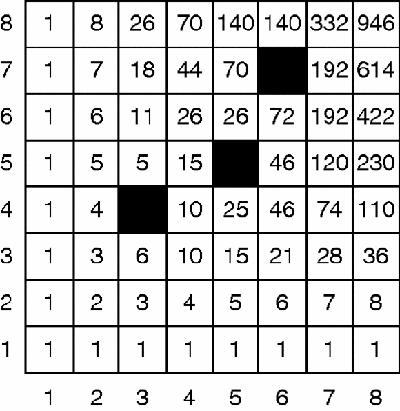
The puzzle is say how many ways there are to move from the lower left cell to the top right cell in as few moves as possible, by always moving from the cell you are on to an adjacent cell, either to right or directly above. We can start a simple mathematical solution by noticing that there are two ways to get to (1,1) but only a single route to either (0,1) or (0,2) or (1,0) or (2,0). Building on this observation we see that there are 1, 3, 3 and only 1 routes to the next diagonal line of cells, and so on (
Figure 5.4
).
Figure 5.4
).
Figure 5.4
Pascal's triangle
Pascal's triangle

By following this pattern we can not only fill in the number of routes to each cell by a rapid and easy calculation, but we can also notice that the resulting pattern is Pascal's triangle
turned on its side:
There is a well-known method of finding the value of any number in any row of this triangle: the number in the
n
th place (from left or right) of the
m
th row is
m
−1
C
n
−1
or (
m
−1)!/(
n
−1)!(
m
−
n
)!. The top-right cell of the original square is actually the middle cell of the 15th row of the triangle, and so it will have the value
14
C
7
= 14·13·12·11·10·9·8/(7·6·5·4·3·2·1) = 3432.
turned on its side:
1 | ||||||
1 | 1 | |||||
1 | 2 | 1 | ||||
1 | 3 | 3 | 1 | |||
1 | 4 | 6 | 4 | 1 | ||
1 | 5 | 10 | 10 | 5 | 1 | |
1 | 6 | 15 | 20 | 15 | 6 | 1 |
[etc.] |
n
th place (from left or right) of the
m
th row is
m
−1
C
n
−1
or (
m
−1)!/(
n
−1)!(
m
−
n
)!. The top-right cell of the original square is actually the middle cell of the 15th row of the triangle, and so it will have the value
14
C
7
= 14·13·12·11·10·9·8/(7·6·5·4·3·2·1) = 3432.
Now that we've ‘seen the light’ this calculation is far quicker than filling in the values of every cell, simple though that was. However, suppose that we now throw a spanner in the works, literally. We delete one of the cells, let's say, (3,4). The goal of the puzzle is the same, to say how many ways there are from (1,1) to (8,8), but without going through (3,4).
On the face of it, this still a perfectly good mathematical puzzle – although the choice of this one square to be avoided does seem highly arbitrary and therefore inelegant – and the solution can still be easily calculated. We just take away from 3432 the number of ways of going from one corner to the other which
do
go through (3,4). That in turn is the number of routes from (0,0) to (3,4) multiplied by the number of routes from (3,4) to (8,8), which equals the number of routes from (1,1) to (6,5). So, after a little thought, the answer to this altered puzzle (
Figure 5.5
) is 3432−10×126 = 2172.
do
go through (3,4). That in turn is the number of routes from (0,0) to (3,4) multiplied by the number of routes from (3,4) to (8,8), which equals the number of routes from (1,1) to (6,5). So, after a little thought, the answer to this altered puzzle (
Figure 5.5
) is 3432−10×126 = 2172.
Figure 5.5
One cell blacked out
One cell blacked out

So far, so good. This is still a mathematical calculation though not as simple or elegant as the solution to the original puzzle. But now suppose that we go further and delete two more squares (
Figures 5.6
).
Figures 5.6
).
Figure 5.6
Three cells blacked out
Three cells blacked out

To answer the same puzzle we now have to subtract from the original total all the routes that go through only one, or only two, or all three of the deleted cells, which means calculating and then subtracting seven different numbers. This is no longer either simple or elegant, and if we go further and deleted, say,
half a dozen cells as in Figure 5.7, then not only is the calculation ridiculously complicated but it would actually be much quicker to check the number of routes by starting at (1,1) and working our way up to (8,8), as we have done in the figure.
half a dozen cells as in Figure 5.7, then not only is the calculation ridiculously complicated but it would actually be much quicker to check the number of routes by starting at (1,1) and working our way up to (8,8), as we have done in the figure.
Figure 5.7
Six cells blacked out
Six cells blacked out

What has happened? Somewhere on the way from the original puzzle to this ‘distorted’ puzzle, the mathematical calculation has become more complicated while the checking solution has become simpler. The mathematical solution has lost its simplicity and elegance and the crude game-like solution has become relatively more efficient.
We can see the same phenomenon in other mathematical recreations. Here is the same chessboard but this time the puzzle is to discover in how many ways
it can be filled with dominoes, that is, pairs of squares glued together complete edge to complete edge (
Figure 5.8
).
it can be filled with dominoes, that is, pairs of squares glued together complete edge to complete edge (
Figure 5.8
).
Figure 5.8
Chessboard and dominoes
Chessboard and dominoes

We can think of this puzzle as a simplified version of Dudeney's original pentomino puzzle. Instead of the 12 pentominoes
with their varied and apparently arbitrary shapes we have simple little dominoes. Surely the question must be easy to answer? Actually, no, it is rather complicated and was first answered by three physicists who were interested in a problem in statistical mechanics and who referred to the dominoes by the physical term
dimers
. Temperley and Fischer together, and also Kasteleyn, proved in 1961 that the number of ways of filling an
m
by
n
rectangle with
mn
/2 dominoes is:
 The apparently simple original puzzle has produced a really complicated formula – including cosines and π – which applies, however, only to rectangles with at least one side even. Suppose that we try to count the ways of filling an odd-odd rectangle with dimers, inevitably leaving one cell empty (
The apparently simple original puzzle has produced a really complicated formula – including cosines and π – which applies, however, only to rectangles with at least one side even. Suppose that we try to count the ways of filling an odd-odd rectangle with dimers, inevitably leaving one cell empty (
Figure 5.9
)?
with their varied and apparently arbitrary shapes we have simple little dominoes. Surely the question must be easy to answer? Actually, no, it is rather complicated and was first answered by three physicists who were interested in a problem in statistical mechanics and who referred to the dominoes by the physical term
dimers
. Temperley and Fischer together, and also Kasteleyn, proved in 1961 that the number of ways of filling an
m
by
n
rectangle with
mn
/2 dominoes is:

Figure 5.9
)?
Figure 5.9
Odd chessboard with dominoes and 1 empty cell
Odd chessboard with dominoes and 1 empty cell

All at once the puzzle becomes far more complex – not least because the position of the empty cell can vary – and less symmetrical and therefore less elegant. Indeed, there is no known formula for the number of dimer patterns
with an arbitrary odd cell deleted and as for deleting a number of cells at random as we did for the first problem – don't ask! Instead, as the number of deleted cells increases, it becomes easier and easier to
check
the number of solutions even as a
proof
becomes a more and more distant prospect.
with an arbitrary odd cell deleted and as for deleting a number of cells at random as we did for the first problem – don't ask! Instead, as the number of deleted cells increases, it becomes easier and easier to
check
the number of solutions even as a
proof
becomes a more and more distant prospect.
It seems that as we add an element of arbitrariness to mathematical problems – an element that is present from the start in many mathematical recreations and which perhaps contributes to their fascination – the possibilities of proof fall and the inevitability of relying for solutions on checking and brute force, rise. We would like to think that behind every problem there is some – maybe very deep and very subtle – structure which guarantees that a more or less short and efficient proof can be found, but this may be over-optimistic.
Other books
Guns and Roses by Brennan, Allison, Armstrong, Lori G., Day, Sylvia
Stiltskin (Andrew Buckley) by Andrew Buckley
Blood of Paradise by David Corbett
Snowbound in Montana by C. J. Carmichael
The Ruling Sea by Robert V. S. Redick
Barbara Metzger by The Duel
Play Along by Mathilde Watson
Mating the Dragon (Dragon Ruins Book 6) by Rinelle Grey
Lone Wolf by Lasky, Kathryn
Scarlett White by Chloe Smith
