Games and Mathematics (34 page)
Read Games and Mathematics Online
Authors: David Wells

Euclidean coordinate geometry
The average of two points
Plane
geometry is so rich because positions can vary
independently
in two dimensions. It was René Descartes (1596–1650) who explained that all the points of the plane could be represented by measurements along two independent axes, the coordinates of the point. By choosing a specific relationship between the coordinates, the point would move in a straight line, or in a circular motion, or along a parabola
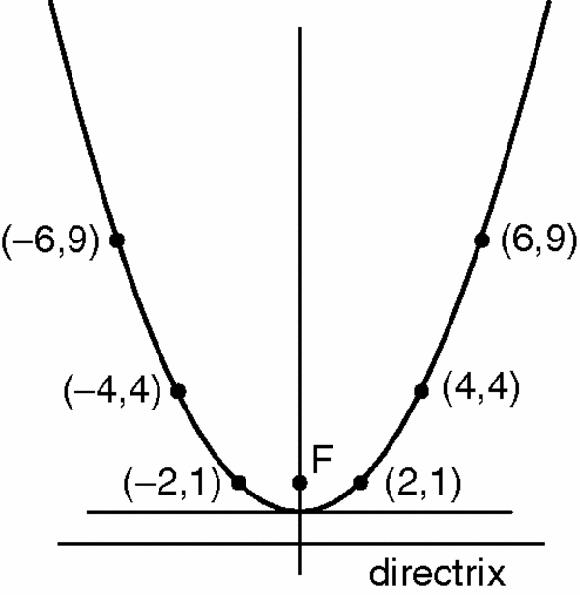
. Figure
17.10
shows the parabola 4
y
=
x
2
.
geometry is so rich because positions can vary
independently
in two dimensions. It was René Descartes (1596–1650) who explained that all the points of the plane could be represented by measurements along two independent axes, the coordinates of the point. By choosing a specific relationship between the coordinates, the point would move in a straight line, or in a circular motion, or along a parabola
. Figure
17.10
shows the parabola 4
y
=
x
2
.
Figure 17.10
Parabola with points marked
Parabola with points marked

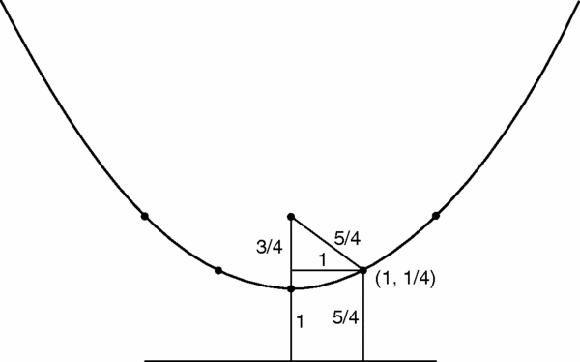
The focus is at (0, 1) and the directrix is the line y = −1. Any point on the parabola is equidistant from each. For example, the point, (1, 1/4) is 5/4 from each, as we find by Pythagoras (Figure
17.11
).
17.11
).
Figure 17.11
Parabola, points marked and focus-directrix property
Parabola, points marked and focus-directrix property

When the plane is covered by a grid of unit squares, Pythagoras' theorem becomes the statement that the square of the distance between two points (a,b) and (c,d) is (a−c)
2
+(b−d)
2
and so the distance PQ =
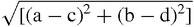 . This is neat but also rather complicated – it includes squares and square roots – which is surprising given how simple the theorem seemed at the end of the last chapter. It suggests that there may be occasions when we should try to
. This is neat but also rather complicated – it includes squares and square roots – which is surprising given how simple the theorem seemed at the end of the last chapter. It suggests that there may be occasions when we should try to
avoid
using Pythagoras, fundamental thought it is, when using coordinate geometry.
2
+(b−d)
2
and so the distance PQ =
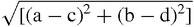 . This is neat but also rather complicated – it includes squares and square roots – which is surprising given how simple the theorem seemed at the end of the last chapter. It suggests that there may be occasions when we should try to
. This is neat but also rather complicated – it includes squares and square roots – which is surprising given how simple the theorem seemed at the end of the last chapter. It suggests that there may be occasions when we should try toavoid
using Pythagoras, fundamental thought it is, when using coordinate geometry.
That conclusion has an element of truth, which emphasises that the type of geometry you use ought to be chosen to
fit the problem
. Let's look at two examples. The first shows the coordinate approach working well, despite first impressions. The second show it working very well indeed on a problem that involves lengths but does not use Pythagoras.
fit the problem
. Let's look at two examples. The first shows the coordinate approach working well, despite first impressions. The second show it working very well indeed on a problem that involves lengths but does not use Pythagoras.
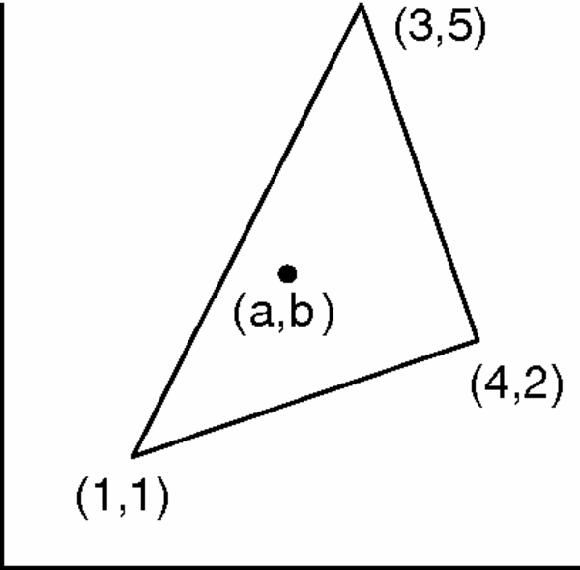
For our first example, let's find the circumcentre of a triangle, the point that is equidistant from all three vertices.
Figure 17.12
Triangle, vertices marked and circumcentre
Triangle, vertices marked and circumcentre

If the circumcentre of the triangle in Figure
17.12
is (a,b) then by Pythagoras's theorem in coordinates we have the equations,
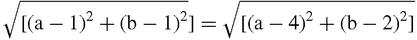
17.12
is (a,b) then by Pythagoras's theorem in coordinates we have the equations,
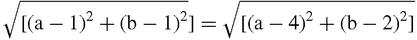
and
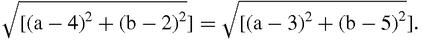 This is only superficially complicated: when we square each equation and simplify and we get the equations of two straight lines:
This is only superficially complicated: when we square each equation and simplify and we get the equations of two straight lines:
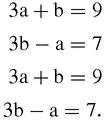
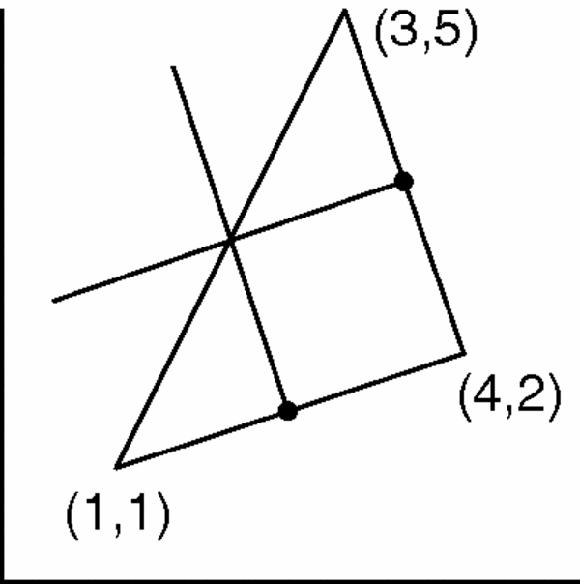
These are the perpendicular bisectors of two of the sides (so we could have found them without using Pythagoras at all, Figure
17.13
) and their intersection happens to lie on the third side because this triangle is right-angled.
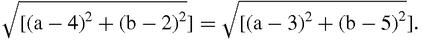
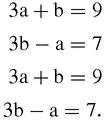
17.13
) and their intersection happens to lie on the third side because this triangle is right-angled.
Figure 17.13
The same triangle with two perpendicular bisectors marked
The same triangle with two perpendicular bisectors marked

In the next case Pythagoras simply can't be used, but we still get a result.
The coordinates of the mid-point of the line joining two points is the arithmetical ‘average’ of their coordinates, and also the
centre of gravity
of the two points, regarded as identical physical particles.
centre of gravity
of the two points, regarded as identical physical particles.
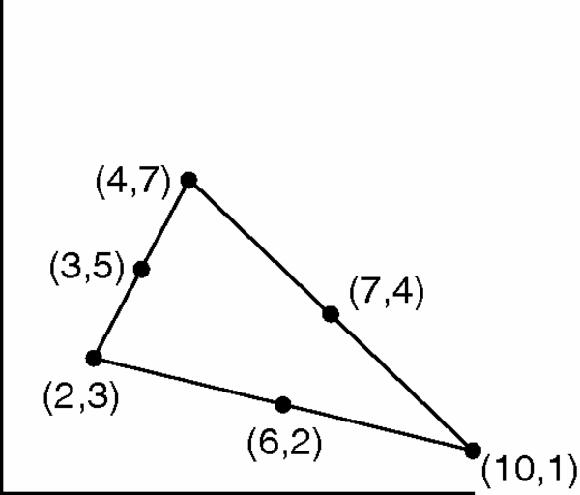
Figure 17.14
Triangle, vertices and mid-points marked
Triangle, vertices and mid-points marked

In Figure
17.14
the ‘average’ of A(2,3) and B(4,7) is (3,5) because 3 is the average of 2 and 4 and 5 is the average of 3 and 7. The three mid-points form a new triangle (
Figure 17.15
). We can now find the mid- points of the sides of that triangle, and then repeat, again and again. The second set of mid-points, by a simple calculation, is (4
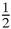 , 3
, 3
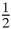 ), (5, 4
), (5, 4
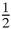 ) and (6
) and (6
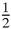 , 3).
, 3).
17.14
the ‘average’ of A(2,3) and B(4,7) is (3,5) because 3 is the average of 2 and 4 and 5 is the average of 3 and 7. The three mid-points form a new triangle (
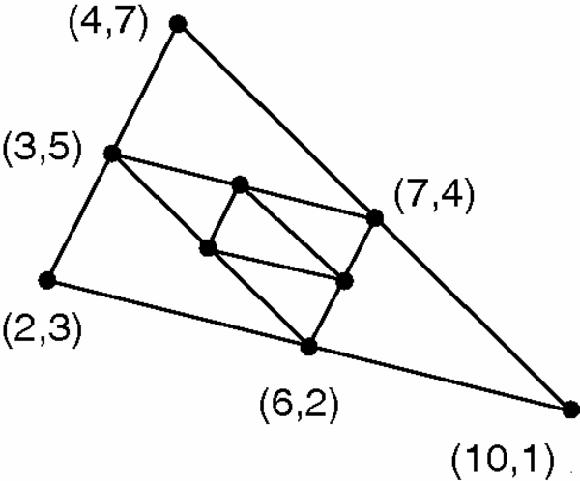
Figure 17.15
). We can now find the mid- points of the sides of that triangle, and then repeat, again and again. The second set of mid-points, by a simple calculation, is (4
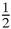 , 3
, 3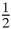 ), (5, 4
), (5, 4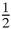 ) and (6
) and (6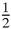 , 3).
, 3).Figure 17.15
The same with mid-points of mid-points marked
The same with mid-points of mid-points marked

We are clearly closing in on ‘a centre’ of the triangle, but which of the centres will it be, and what are its coordinates? By finding averages repeatedly,
we only get what is called a
linear function
of the numbers we started with, meaning no squares, cubes, square roots, and so on. Also, our calculations are symmetrical, so the result must depend symmetrically on the original three points, but the only symmetrical linear function of A, B and C is their sum, A + B + C or a fraction or multiple of it. In fact, the limit of all these triangles is 1/3(A + B + C) which, calculating for each coordinate separately, is (16/3, 11/3). This is, as we might have guessed, the centre of gravity of the vertices of all three triangles.
we only get what is called a
linear function
of the numbers we started with, meaning no squares, cubes, square roots, and so on. Also, our calculations are symmetrical, so the result must depend symmetrically on the original three points, but the only symmetrical linear function of A, B and C is their sum, A + B + C or a fraction or multiple of it. In fact, the limit of all these triangles is 1/3(A + B + C) which, calculating for each coordinate separately, is (16/3, 11/3). This is, as we might have guessed, the centre of gravity of the vertices of all three triangles.
Other books
Raw Deal (Bite Back) by Mark Henwick
A Sister's Hope by Wanda E. Brunstetter
Buried Bones by Carolyn Haines
Cat of a Different Color: Halle Pumas, Book 3 by Dana Marie Bell
Terms of Service by Emma Nichols
True Colors by Joyce Lamb
Nothing Lasts Forever by Sidney Sheldon
The Last Days of Marilyn Monroe by Donald H. Wolfe
You Don't Sweat Much for a Fat Girl by Rivenbark, Celia
