Hyperspace (17 page)
Authors: Michio Kaku,Robert O'Keefe

Riemann’s great contribution, we recall, was that he introduced the concept of the metric tensor, a field that is defined at all points in space. The metric tensor is not a single number. At each point in space, it consists of a collection of ten numbers. Einstein’s strategy was to follow Maxwell and write down the field theory of gravity. The object of his search for a field to describe gravity was found practically on the first
page of Riemann’s lecture. In fact, Riemann’s metric tensor was precisely the Faraday field for gravity!
When Einstein’s equations are fully expressed in terms of Riemann’s metric tensor, they assume an elegance never before seen in physics. Nobel laureate Subrahmanyan Chandrasekhar once called it “the most beautiful theory there ever was.” (In fact, Einstein’s theory is so simple yet so powerful that physicists are sometimes puzzled as to why it works so well. MIT physicist Victor Weisskopf once said, “It’s like the peasant who asks the engineer how the steam engine works. The engineer explains to the peasant exactly where the steam goes and how it moves through the engine and so on. And then the peasant says: ‘Yes, I understand all that, but where is the horse?’ That’s how I feel about general relativity. I know all the details, I understand where the steam goes, but I’m still not sure I know where the horse is.”
9
)
In retrospect, we now see how close Riemann came to discovering the theory of gravity 60 years before Einstein. The entire mathematical apparatus was in place in 1854. His equations were powerful enough to describe the most complicated twisting of space-time in any dimension. However, he lacked the physical picture (that matter-energy determines the curvature of space-time) and the keen physical insight that Einstein provided.
I once attended a hockey game in Boston. All the action, of course, was concentrated on the hockey players as they glided on the ice rink. Because the puck was being rapidly battered back and forth between the various players, it reminded me of how atoms exchange electrons when they form chemical elements or molecules. I noticed that the skating rink, of course, did not participate in the game. It only marked the various boundaries; it was a passive arena on which the hockey players scored points.
Next, I imagined what it must be like if the skating rink actively participated in the game: What would happen if the players were forced to play on an ice rink whose surface was curved, with rolling hills and steep valleys?
The hockey game would suddenly became more interesting. The players would have to skate along a curved surface. The rink’s curvature would distort their motion, acting like a “force” pulling the players one
way or another. The puck would move in a curved line like a snake, making the game much more difficult.
Then I imagined taking this one step further; I imagined that the players were forced to play on a skating rink shaped like a cylinder. If the players could generate enough speed, they could skate upside down and move entirely around the cylinder. New strategies could be devised, such as ambushing an opposing player by skating upside down around the cylinder and catching him unawares. Once the ice rink was bent in the shape of a circle, space would become the decisive factor in explaining the motion of matter on its surface.
Another, more relevant example for our universe might be living in a curved space given by a hypersphere, a sphere in four dimensions.
10
If we look ahead, light will circle completely around the small perimeter of the hypersphere and return to our eyes. Thus we will see someone standing in front of us, with his back facing us, a person who is wearing the same clothes as we are. We look disapprovingly at the unruly, unkempt mass of hair on this person’s head, and then remember that we forgot to comb our hair that day.
Is this person a fake image created by mirrors? To find out, we stretch out our hand and put it on his shoulder. We find that the person in front of us is a real person, not just a fake. If we look into the distance, in fact, we see an infinite number of identical people, each facing forward, each with his hand on the shoulder of the person in front.
But what is most shocking is that we feel someone’s hand sneaking up from behind, which then grabs our shoulder. Alarmed, we look back, and see another infinite sequence of identical people behind us, with their faces turned the other way.
What’s really happening? We, of course, are the only person living in this hypersphere. The person in front of us is really ourself. We are staring at the back of our own head. By placing our hand in front of us, we are really stretching our hand around the hypersphere, until we place our hand on our own shoulder.
The counterintuitive stunts that are possible in a hypersphere are physically interesting because many cosmologists believe that our universe is actually a large hypersphere. There are also other equally strange topologies, like hyperdoughnuts and Möbius strips. Although they may ultimately have no practical application, they help to illustrate many of the features of living in hyperspace.
For example, let us assume that we are living on a hyperdoughnut. If we look to our left and right, we see, much to our surprise, a person on either side. Light circles completely around the larger perimeter of
the doughnut, and returns to its starting point. Thus if we turn our heads and look to the left, we see the right side of someone’s body. By turning our heads the other way, we see someone’s left side. No matter how fast we turn our heads, the people ahead of us and to our sides turn their heads just as fast, and we can never see their faces.
Now imagine stretching our arms to either side. Both the person on the left and the one on the right will also stretch their arms. In fact, if you are close enough, you can grab the left and right hands of the persons to either side. If you look carefully in either direction, you can see an infinitely long, straight line of people all holding hands. If you look ahead, there is another infinite sequence of people standing before you, arranged in a straight line, all holding hands.
What’s actually happening? In reality our arms are long enough to reach around the doughnut, until the arms have touched. Thus we have actually grabbed our own hands (
Figure 4.2
)!
Now we find ourselves tiring of this charade. These people seem to be taunting us; they are copy-cats, doing exactly what we do. We get annoyed—so we get a gun and point it at the person in front of us. Just before we pull the trigger, we ask ourselves: Is this person a fake mirror image? If so, then the bullet will go right through him. But if not, then the bullet will go completely around the universe and hit us in the back. Maybe firing a gun in this universe is not such a good idea!
For an even more bizarre universe, imagine living on a Möbius strip, which is like a long strip of paper twisted 180 degrees and then reglued back together into a circular strip. When a right-handed Flatlander moves completely around the Möbius strip, he finds that he has become left-handed. Orientations are reversed when traveling around the universe. This is like H. G. Wells’s “The Plattner Story,” in which the hero returns to earth after an accident to find that his body is completely reversed; for example, his heart is on his right side.
If we lived on a hyper-Möbius strip, and we peered in front of us, we would see the back of someone’s head. At first, we wouldn’t think it could be our head, because the part of the hair would be on the wrong side. If we reached out and placed our right hand on his shoulder, then he would lift up his left hand and place it on the shoulder of the person ahead of him. In fact, we would see an infinite chain of people with hands on each other’s shoulders, except the hands would alternate from the left to the right shoulders.
If we left some of our friends at one spot and walked completely around this universe, we would find that we had returned to our original spot. But our friends would be shocked to find that our body was reversed. The part in our hair and the rings on our fingers would be on the wrong side, and our internal organs would have been reversed. Our friends would be amazed at the reversal of our body, and would ask if we felt well. In fact, we would feel completely normal; to us, it would be our friends who had been completely turned around! An argument would now ensue over who was really reversed.
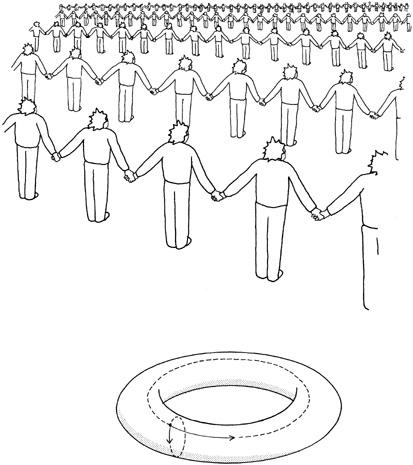
Figure 4.2. If we lived in a hyperdoughnut, we would see an infinite succession of ourselves repeated in front of us, to the back of us, and to our sides. This is because there are two ways that light can travel around the doughnut If we hold hands with the people to our sides, we are actually holding our own hands; that is, our arms are actually encircling the doughnut
.
These and other interesting possibilities open up when we live in a universe where space and time are curved. No longer a passive arena, space becomes an active player in the drama unfolding in our universe.
In summary, we see that Einstein fulfilled the program initiated by Riemann 60 years earlier, to use higher dimensions to simplify the laws of nature. Einstein, however, went beyond Riemann in several ways. Like Riemann before him, Einstein independently realized that “force” is a consequence of geometry, but unlike Riemann, Einstein was able to find the physical principle behind this geometry, that the curvature of space-time is due to the presence of matter-energy. Einstein, also like Riemann, knew that gravitation can be described by a field, the metric tensor, but Einstein was able to find the precise field equations that these fields obey.
By the mid-1920s, with the development of both special and general relativity, Einstein’s place in the history of science was assured. In 1921, astronomers had verified that starlight indeed bends as it travels around the sun, precisely as Einstein had predicted. By then, Einstein was being celebrated as the successor to Isaac Newton.
However, Einstein still was not satisfied. He would try one last time to produce another world-class theory. But on his third try, he failed. His third and final theory was to have been the crowning achievement of his lifetime. He was searching for the “theory of everything,” a theory that would explain all the familiar forces found in nature, including light and gravity. He coined this theory the
unified field theory
. Alas, his search for a unified theory of light and gravity was fruitless. When he died, he left only the unfinished ideas of various manuscripts on his desk.
Ironically, the source of Einstein’s frustration was the structure of his own equation. For 30 years, he was disturbed by a fundamental flaw in this formulation. On one side of the equation was the curvature of space-time, which he likened to “marble” because of its beautiful geometric structure. To Einstein, the curvature of space-time was like the epitome of Greek architecture, beautiful and serene. However, he hated the other side of this equation, describing matter-energy, which he considered to be ugly and which he compared to “wood.” While the “marble” of space-time was clean and elegant, the “wood” of matter-energy was a horrible jumble of confused, seemingly random forms, from subatomic particles, atoms, polymers, and crystals to rocks, trees, planets,
and stars. But in the 1920s and 1930s, when Einstein was actively working on the unified field theory, the true nature of matter remained an unsolved mystery.
Einstein’s grand strategy was to turn wood into marble—that is, to give a completely geometric origin to matter. But without more physical clues and a deeper physical understanding of the wood, this was impossible. By analogy, think of a magnificent, gnarled tree growing in the middle of a park. Architects have surrounded this grizzled tree with a plaza made of beautiful pieces of the purest marble. The architects have carefully assembled the marble pieces to resemble a dazzling floral pattern with vines and roots emanating from the tree. To paraphrase Mach’s principle: The presence of the tree determines the pattern of the marble surrounding it. But Einstein hated this dichotomy between wood, which seemed to be ugly and complicated, and marble, which was simple and pure. His dream was
to turn the tree into marble;
he would have liked to have a plaza completely made of marble, with a beautiful, symmetrical marble statue of a tree at its center.
In retrospect, we can probably spot Einstein’s error. We recall that the laws of nature simplify and unify in higher dimensions. Einstein correctly applied this principle twice, in special and general relativity. However, on his third try, he abandoned this fundamental principle. Very little was known about the structure of atomic and nuclear matter in his time; consequently, it was not clear how to use higher-dimensional space as a unifying principle.
Einstein blindly tried a number of purely mathematical approaches. He apparently thought that “matter” could be viewed as kinks, vibrations, or distortions of space-time. In this picture, matter was a concentrated distortion of space. In other words, everything we see around us, from the trees and clouds to the stars in the heavens, was probably an illusion, some form of crumpling of hyperspace. However, without any more solid leads or experimental data, this idea led to a blind alley.
