Hyperspace (18 page)

It would be left to an obscure mathematician to take the next step, which would lead us to the fifth dimension.

In April 1919, Einstein received a letter that left him speechless.

It was from an unknown mathematician, Theodr Kaluza, at the University of Königsberg in Germany, in what is Kaliningrad in the former Soviet Union. In a short article, only a few pages long, this obscure mathematician
was proposing a solution to one of the greatest problems of the century. In just a few lines, Kaluza was uniting Einstein’s theory of gravity with Maxwell’s theory of light by introducing the
fifth
dimension (that is, four dimensions of space and one dimension of time).

In essence, he was resurrecting the old “fourth dimension” of Hinton and Zollner and incorporating it into Einstein’s theory in a fresh fashion as the fifth dimension. Like Riemann before him, Kaluza assumed that light is a disturbance caused by the rippling of this higher dimension. The key difference separating this new work from Riemann’s, Hinton’s, and Zollner’s was that Kaluza was proposing a genuine field theory.

In this short note, Kaluza began, innocently enough, by writing down Einstein’s field equations for gravity in five dimensions, not the usual four. (Riemann’s metric tensor, we recall, can be formulated in any number of dimensions.) Then he proceeded to show that these five-dimensional equations contained within them Einstein’s earlier four-dimensional theory (which was to be expected) with an additional piece. But what shocked Einstein was that this additional piece was precisely Maxwell’s theory of light. In other words, this unknown scientist was proposing to combine, in one stroke, the two greatest field theories known to science, Maxwell’s and Einstein’s, by mixing them in the fifth dimension. This was a theory made of pure marble—that is, pure geometry.

Kaluza had found the first important clue in turning wood into marble. In the analogy of the park, we recall that the marble plaza is two dimensional. Kaluza’s observation was that we could build a “tree” of marble if we could move the pieces of marble
up
into the third dimension.

To the average layman, light and gravity have nothing in common. After all, light is a familiar force that comes in a spectacular variety of colors and forms, while gravity is invisible and more distant. On the earth, it is the electromagnetic force, not gravity, that has helped us tame nature; it is the electromagnetic force that powers our machines, electrifies our cities, lights our neon signs, and brightens our television sets. Gravity, by contrast, operates on a larger scale; it is the force that guides the planets and keeps the sun from exploding. It is a cosmic force that permeates the universe and binds the solar system. (Along with Weber and Riemann, one of the first scientists to search actively for a link between light and gravity in the laboratory was Faraday himself. The actual experimental apparatus used by Faraday to measure the link between these two forces can still be found in the Royal Institution in Piccadilly, London. Although he failed experimentally to find any connection
at all between the two forces, Faraday was confident of the power of unification. He wrote, “If the hope [of unification] should prove well founded, how great and mighty and sublime in its hitherto unchangeable character is the force I am trying to deal with, and how large may be the new domain of knowledge that may be opened to the mind of man.”
¹¹
)

Even mathematically, light and gravity are like oil and water. Maxwell’s field theory of light requires four fields, while Einstein’s metric theory of gravity requires ten. Yet Kaluza’s paper was so elegant and compelling that Einstein could not reject it.

At first, it seemed like a cheap mathematical trick simply to expand the number or dimensions of space and time from four to five. This was because, as we recall, there was no experimental evidence for the fourth spatial dimension. What astonished Einstein was that once the five-dimensional field theory was broken down to a four-dimensional field theory, both Maxwell’s and Einstein’s equations remained. In other words, Kaluza succeeded in joining the two pieces of the jigsaw puzzle because both of them were part of a larger whole, a five-dimensional space.

“Light” was emerging as the warping of the geometry of higher-dimensional space. This was the theory that seemed to fulfill Riemann’s old dream of explaining forces as the crumpling of a sheet of paper. In his article, Kaluza claimed that his theory, which synthesized the two most important theories up to that time, possessed “virtually unsurpassed formal unity.” He furthermore insisted that the sheer simplicity and beauty of his theory could not “amount to the mere alluring play of a capricious accident.”
¹²
What shook Einstein was the audacity and simplicity of the article. Like all great ideas, Kaluza’s essential argument was elegant and compact.

The analogy with piecing together the parts of a jigsaw puzzle is a meaningful one. Recall that the basis of Riemann’s and Einstein’s work is the metric tensor—that is, a collection of ten numbers defined at each point in space. This was a natural generalization of Faraday’s field concept. In
Figure 2.2
, we saw how these ten numbers can be arranged as in the pieces of a checker board with dimensions 4 × 4. We can denote these ten numbers as g
₁₁
, g
₁₂
,…. Furthermore, the field of Maxwell is a collection of four numbers defined at each point in space. These four numbers can be represented by the symbols
A
₁
,
A
₂
,
A
₃
,
A
₄
.

To understand Kaluza’s trick, let us now begin with Riemann’s theory in five dimensions. Then the metric tensor can be arranged in a 5 × 5 checkerboard. Now, by definition, we will rename the components of Kaluza’s field, so that some of them become Einstein’s original field and some of them become Maxwell’s field (
Figure 4.3
). This is the essence of Kaluza’s trick, which caught Einstein totally by surprise. By simply adding Maxwell’s field to Einstein’s, Kaluza was able to reassemble both of them into a five-dimensional field.

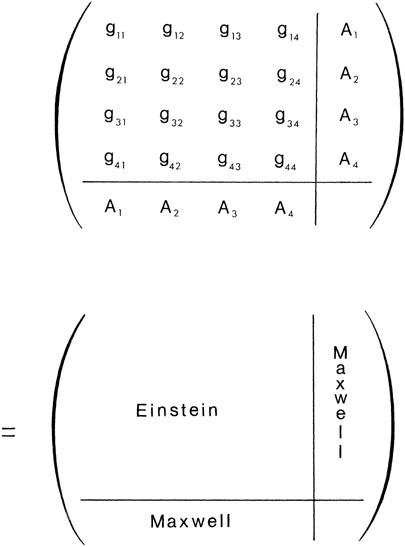
Figure 4.3. Kaluza’s brilliant idea was to write down the Riemann metric in five dimensions. The fifth column and row are identified as the electromagnetic field of Maxwell, while the remaining 4 × 4 block is the old four-dimensional metric of Einstein. In one stroke, Kaluza unified the theory of gravity with light simply by adding another dimension
.

Notice that there is “enough room” within the 15 components of Riemann’s five-dimensional gravity to fit both the ten components of Einstein’s field and the four components of Maxwell’s field! Thus Kaluza’s brilliant idea can be crudely summarized as

15 = 10 + 4 + 1

(the leftover component is a scalar particle, which is unimportant for our discussion). When carefully analyzing the full five-dimensional theory, we find that Maxwell’s field is nicely included within the Riemann metric tensor, just as Kaluza claimed. This innocent-looking equation thus summarized one of the seminal ideas of the century.

In summary, the five-dimensional metric tensor included both Maxwell’s field and Einstein’s metric tensor. It seemed incredible to Einstein that such a simple idea could explain the two most fundamental forces of nature: gravity and light.

Was it just a parlor trick? Or numerology? Or black magic? Einstein was deeply shaken by Kaluza’s letter and, in fact, refused to respond to the article. He mulled over the letter for 2 years, an unusually long time for someone to hold up publication of an important article. Finally, convinced that this article was potentially important, he submitted it for publication in the
Sitzungsberichte Preussische Akademie der Wissenschaften
. It bore the imposing title “On the Unity Problem of Physics.”

In the history of physics, no one had found any use for the fourth spatial dimension. Ever since Riemann, it was known that the mathematics of higher dimensions was one of breathtaking beauty, but without physical application. For the first time, someone had found a use for the fourth spatial dimension: to unite the laws of physics! In some sense, Kaluza was proposing that the four dimensions of Einstein were “too small” to accommodate both the electromagnetic and gravitational forces.

We can also see historically that Kaluza’s work was not totally unexpected. Most historians of science, when they mention Kaluza’s work at all, say that the idea of a fifth dimension was a bolt out of the blue, totally unexpected and original. Given the continuity of physics research, these historians are startled to find a new avenue of science opening up without
any historical precedent. But their amazement is probably due to their unfamiliarity with the nonscientific work of the mystics, literati, and avante garde. A closer look at the cultural and historical setting shows that Kaluza’s work was not such an unexpected development. As we have seen, because of Hinton, Zollner, and others, the possible existence of higher dimensions was perhaps the single most popular quasi-scientific idea circulating within the arts. From this larger cultural point of view, it was only a matter of time before some physicist took seriously Hinton’s widely known idea that light is a vibration of the fourth spatial dimension. In this sense, the work of Riemann pollinated the world of arts and letters via Hinton and Zollner, and then probably cross-pollinated back into the world of science through the work of Kaluza. (In support of this thesis, it was recently revealed by Freund that Kaluza was actually not the first one to propose a five-dimensional theory of gravity. Gunnar Nordstrom, a rival of Einstein, actually published the first five-dimensional field theory, but it was too primitive to include both Einstein’s and Maxwell’s theories. The fact that both Kaluza and Nordstrom independently tried to exploit the fifth dimension indicates that the concepts widely circulating within popular culture affected their thinking.
¹³
)

Every physicist receives quite a jolt when confronting the fifth dimension for the first time. Peter Freund remembers clearly the precise moment when he first encountered the fifth and higher dimensions. It was an event that left a deep impression on his thinking.

It was 1953 in Romania, the country of Freund’s birth. Joseph Stalin had just died, an important event that led to a considerable relaxation of tensions. Freund was a precocious college freshman that year, and he attended a talk by George Vranceanu. He vividly remembers hearing Vranceanu discuss the important question: Why should light and gravity be so disparate? Then the lecturer mentioned an old theory that could contain both the theory of light and Einstein’s equations of gravity. The secret was to use Kaluza-Klein theory, which was formulated in five dimensions.

Freund was shocked. Here was a brilliant idea that took him completely by surprise. Although only a freshman, he had the audacity to pose the obvious question: How does this Kaluza-Klein theory explain the other forces? He asked, “Even if you achieve a unification of light
and gravity, you will not achieve anything because there is still the nuclear force.” He realized that the nuclear force was outside Kaluza-Klein theory. (In fact, the hydrogen bomb, which hung like a sword over everyone on the planet at the height of the Cold War, was based on unleashing the nuclear force, not electromagnetism or gravity.)

The lecturer had no answer. In his youthful enthusiasm, Freund blurted out, “What about adding more dimensions?”

“But how many more dimensions?” asked the lecturer.

Freund was caught off guard. He did not want to give a low number of dimensions, only to be scooped by someone else. So he proposed a number that no one could possibly top: an infinite number of dimensions!
¹⁴
(Unfortunately for this precocious physicist, an infinite number of dimensions does not seem to be physically possible.)

After the initial shock of confronting the fifth dimension, most physicists invariably begin to ask questions. In fact, Kaluza’s theory raised more questions than it answered. The obvious question to ask Kaluza was: Where is the fifth dimension? Since all earthly experiments showed conclusively that we live in a universe with three dimensions of space and one of time, the embarrassing question still remained.

Kaluza had a clever response. His solution was essentially the same as that proposed by Hinton years before, that the higher dimension, which was not observable by experiment, was different from the other dimensions. It had, in fact, collapsed down to a circle so small that even atoms could not fit inside it. Thus the fifth dimension was not a mathematical trick introduced to manipulate electromagnetism and gravity, but a physical dimension that provided the glue to unite these two fundamental forces into one force, but was just too small to measure.

Anyone walking in the direction of the fifth dimension would eventually find himself back where he started. This is because the fifth dimension is topologically identical to a circle, and the universe is topologically identical to a cylinder.