In Pursuit of the Unknown (22 page)

Fig 28
Reidemeister moves.

With some preliminary fiddling to tidy up the knot diagram, such as modifying places where three curves overlap if that ever happens, it can be proved that any deformation of a knot can be represented as a finite series of Reidemeister moves applied to its diagram. Now we can play the Euler game; all we have to do is find an invariant. Among them is the knot group, but there is a far simpler invariant that proves the trefoil really is a knot. I can explain it in terms of colouring the separate components in a knot diagram. I'm starting with a slightly more complicated diagram than I have to, with an extra loop, in order to illustrate some features of the idea,
Figure 29
.

Fig 29
Colouring a trefoil knot with an extra twist.

The extra twist creates four separate components. Suppose I colour the components using three colours for each, say red, yellow, and blue (shown in the figure as black, light grey, and dark grey). Then this colouring obeys two simple rules:

•
At least two distinct colours are used. (Actually all three are, but that's extra information that I don't need.)

•
At each crossing, either the three strands near the crossing all have different colours or they are all the same colour. Near the crossing caused by my extra loop, all three components are yellow. Two of these components (in yellow) join up elsewhere, but near the crossing they are separate.

The wonderful observation is that if a knot diagram can be coloured using three colours, obeying these two rules, then the same is true after any Reidemeister move. You can prove this very easily by working out how the Reidemeister moves affect the colours. For example, if I untwist the extra loop in my picture then I can leave the colours unchanged and everything still works. Why is this wonderful? Because it proves that the trefoil really is knotted. Suppose for the sake of argument that it can be unknotted; then some series of Reidemeister moves turns it into an unknotted loop. Since the trefoil can be coloured to obey the two rules, the same must apply to
the unknotted loop. But an unknotted loop consists of a single strand with no overlaps, so the only way to colour it is to use the same colour everywhere. But this violates the first rule. By contradiction, no such series of Reidemeister moves can exist; that is, the trefoil can't be unknotted.

This proves that the trefoil is knotted, but doesn't distinguish it from other knots such as the reef knot or the stevedore's knot. One of the earliest effective ways to do this was invented by Alexander. It was derived from Reidemeister's abstract algebra methods, but it leads to an invariant that is algebraic in the more familiar sense of school algebra. It's called the Alexander polynomial, and it associates to any knot a formula formed from powers of a variable
x
. Strictly speaking, the term ‘polynomial' applies only when the powers are positive integers, but here we also allow negative powers.
Table 2
lists a few Alexander polynomials. If two knots in the list have different Alexander polynomials, and here all but the reef and granny do, then the knots must be topologically different. The converse is not true: the reef and granny have the same Alexander polynomials, but in 1952 Ralph Fox proved that they are topologically different. The proof required surprisingly sophisticated topology. It was far more difficult than anyone expected.

Table 2
Alexander polynomials of knots.

After about 1960 knot theory entered the topological doldrums, becalmed in a vast ocean of unsolved questions, awaiting a breath of creative insight. It came in 1984, when the New Zealand mathematician Vaughan Jones had an idea so simple that it could have occurred to anyone from Reidemeister onwards. Jones wasn't a knot theorist; he wasn't even a topologist. He was an analyst, working on operator algebras, an area with strong links to mathematical physics. It wasn't a total surprise that the ideas applied to knots, because mathematicians and physicists already knew of interesting connections between operator algebras and braids,
which are a special kind of multi-stranded knot. The new knot invariant he invented, called the Jones polynomial, is also defined using the knot diagram and three types of move. However, the moves do not preserve the topological type of the knot; they do not preserve the new ‘Jones polynomial'. Amazingly, however, the idea can still be made to work, and the Jones polynomial is a knot invariant.

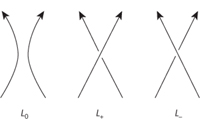
Fig 30
Jones moves.

For this invariant we have to choose a specific direction along the knot, shown by an arrow. The Jones polynomial
V
(
x
) is defined to be one for the unknot. Given any knot L
₀
, move two separate strands close together without changing any crossings in its diagram. Be careful to align the directions as shown: that's why the arrow is needed, and the process doesn't work without it. Replace that region of L
₀
by two strands that cross in the two possible ways (
Figure 30
). Let the resulting knot diagrams be L
₊
and
L
_−
. Now define

(
x
^1/2
−
x
^−1/2
)
V
(
L
₀
) =
x
^−1
V
(
L
₊
) −
x
V
(
L
_−
)

By starting with the unknot and applying such moves in the right way, you can work out the Jones polynomial for any knot. Mysteriously, it turns out to be a topological invariant. And it outperforms the traditional Alexander polynomial; for instance, it can distinguish reef from granny, because they have different Jones polynomials.

Jones's discovery won him the Fields medal, the most prestigious prize in mathematics. It also triggered an outburst of new knot invariants. In 1985 four different groups of mathematicians, eight people in total, simultaneously discovered the same generalisation of the Jones polynomial and submitted their papers independently to the same journal. All four proofs were different, and the editor persuaded the eight authors to join forces and publish one combined article. Their invariant is often called the HOMFLY polynomial, based on their initials. But even the
Jones and HOMFLY polynomials have not fully answered the three problems of knot theory. It is not known whether a knot with Jones polynomial 1 must be unknotted, though many topologists think this is probably true. There exist topologically distinct knots with the same Jones polynomial; the simplest examples known have ten crossings in their knot diagrams. A systematic classification of all possible knots remains a mathematician's pipedream.

It's pretty, but is it useful? Topology has many uses, but they are usually indirect. Topological principles provide insight into other, more directly applicable, areas. For instance, our understanding of chaos is founded on topological properties of dynamical systems, such as the bizarre behaviour that Poincaré noted when he rewrote his prizewinning memoir (
Chapter 4
). The Interplanetary Superhighway is a topological feature of the dynamics of the Solar System.

More esoteric applications of topology arise at the frontiers of fundamental physics. Here the main consumers of topology are quantum field theorists, because the theory of superstrings, the hoped-for unification of quantum mechanics and relativity, is based on topology. Here analogues of the Jones polynomial in knot theory arise in the context of Feynman diagrams, which show how quantum particles such as electrons and photons move through space-time, colliding, merging, and breaking apart. A Feynman diagram is a bit like a knot diagram, and Jones's ideas can be extended to this context.

To me one of the most fascinating applications of topology is its growing use in biology, helping us to understand the workings of the molecule of life, DNA. Topology turns up because DNA is a double helix, like two spiral staircases winding around each other. The two strands are intricately intertwined, and important biological processes, in particular the way a cell copies its DNA when it divides, have to take account of this complex topology. When Francis Crick and James Watson published their work on the molecular structure of DNA in 1953 they ended with a brief allusion to a possible copying mechanism, presumably involved in cell division, in which the two strands were pulled apart and each was used as the template for a new copy. They were reluctant to claim too much, because they were aware that there are topological obstacles to pulling apart intertwined strands. Being too specific about their proposal might have muddied the waters at such an early stage.

As things turned out, Crick and Watson were right. The topological
obstacles are real, but evolution has provided methods for overcoming them, such as special enzymes that cut-and-paste strands of DNA. It is no coincidence that one of these is called topoisomerase. In the 1990s mathematicians and molecular biologists used topology to analyse the twists and turns of DNA, and to study how it works in the cell, where the usual method of X-ray diffraction can't be used because it requires the DNA to be in crystalline form.

Fig 31
Loop of DNA forming a trefoil knot.

Some enzymes, called recombinases, cut the two DNA strands and rejoin them in a different way. To determine how such an enzyme acts when it is in a cell, biologists apply the enzyme to a closed loop of DNA. Then they observe the shape of the modified loop using an electron microscope. If the enzyme joins distinct strands together, the image is a knot,
Figure 31
. If the enzyme keeps the strands separate, the image shows two linked loops. Methods from knot theory, such as the Jones polynomial and another theory known as ‘tangles', make it possible to work out which knots and links occur, and this provides detailed information about what the enzyme does. They also make new predictions that have been verified experimentally, giving some confidence that the mechanism indicated by the topological calculations is correct.
¹