In Pursuit of the Unknown (23 page)

One the whole, you won't run into topology in everyday life, aside from that dishwasher I mentioned at the start of this chapter. But behind the scenes, topology informs the whole of mainstream mathematics, enabling the development of other techniques with more obvious practical uses. This is why mathematicians consider topology to be of vast importance, while the rest of the world has hardly heard of it.

The probability of observing a particular data value is greatest near the mean value – the average – and dies away rapidly as the difference from the mean increases. How rapidly depends on a quantity called the standard deviation.

It defines a special family of bell-shaped probability distributions, which are often good models of common real-world observations.

The concept of the ‘average man', tests of the significance of experimental results, such as medical trials, and an unfortunate tendency to default to the bell curve as if nothing else existed.

M
athematics is about patterns. The random workings of chance seem to be about as far from patterns as you can get. In fact, one of the current definitions of ‘random' boils down to ‘lacking any discernible pattern'. Mathematicians had been investigating patterns in geometry, algebra, and analysis for centuries before they realised that even randomness has its own patterns. But the patterns of chance do not conflict with the idea that random events have no pattern, because the regularities of random events are statistical. They are features of a whole series of events, such as the average behaviour over a long run of trials. They tell us nothing about which event occurs at which instant. For example, if you throw a dice
¹
repeatedly, then about one sixth of the time you will roll 1, and the same holds for 2, 3, 4, 5, and 6 − a clear statistical pattern. But this tells you nothing about which number will turn up on the next throw.

Only in the nineteenth century did mathematicians and scientists realise the importance of statistical patterns in chance events. Even human actions, such as suicide and divorce, are subject to quantitative laws, on average and in the long run. It took time to get used to what seemed at first to contradict free will. But today these statistical regularities form the basis of medical trials, social policy, insurance premiums, risk assessments, and professional sports.

And gambling, which is where it all began.

Appropriately, it was all started by the gambling scholar, Girolamo Cardano. Being something of a wastrel, Cardano brought in much-needed cash by taking wagers on games of chess and games of chance. He applied his powerful intellect to both. Chess does not depend on chance: winning depends on a good memory for standard positions and moves, and an intuitive sense of the overall flow of the game. In a game of chance, however, the player is subject to the whims of Lady Luck. Cardano realised that he could apply his mathematical talents to good effect even in this tempestuous relationship. He could improve his performance at games
of chance by having a better grasp of the odds – the likelihood of winning or losing – than his opponents did. He put together a book on the topic,
Liber de Ludo Aleae
(‘Book on Games of Chance'). It remained unpublished until 1633. Its scholarly content is the first systematic treatment of the mathematics of probability. Its less reputable content is a chapter on how to cheat and get away with it.

One of Cardano's fundamental principles was that in a fair bet, the stakes should be proportional to the number of ways in which each player can win. For example, suppose the players roll a dice, and the first player wins if he throws a 6, while the second player wins if he throws anything else. The game would be highly unfair if each bet the same amount to play the game, because the first player has only one way to win, whereas the second has five. If the first player bets £1 and the second bets £5, however, the odds become equitable. Cardano was aware that this method of calculating fair odds depends on the various ways of winning being equally likely, but in games of dice, cards, or coin-tossing it was clear how to ensure that this condition applied. Tossing a coin has two outcomes, heads or tails, and these are equally likely if the coin is fair. If the coin tends to throw more heads than tails, it is clearly biased – unfair. Similarly the six outcomes for a fair dice are equally likely, as are the 52 outcomes for a card drawn from a pack.

The logic behind the concept of fairness here is slightly circular, because we infer bias from a failure to match the obvious numerical conditions. But those conditions are supported by more than mere counting. They are based on a feeling of symmetry. If the coin is a flat disc of metal, of uniform density, then the two outcomes are related by a symmetry of the coin (flip it over). For dice, the six outcomes are related by symmetries of the cube. And for cards, the relevant symmetry is that no card differs significantly from any other, except for the value written on its face. The frequencies 1/2, 1/6, and 1/52 for any given outcome rest on these basic symmetries. A biased coin or biased dice can be created by the covert insertion of weights; a biased card can be created using subtle marks on the back, which reveal its value to those in the know.

There are other ways to cheat, involving sleight of hand – say, to swap a biased dice into and out of the game before anyone notices that it always throws a 6. But the safest way to ‘cheat' – to win by subterfuge – is to be perfectly honest, but to know the odds better than your opponent. In one sense you are taking the moral high ground, but you can improve your chances of finding a suitably naive opponent by rigging not the odds but your opponent's expectation of the odds. There are many examples where
the actual odds in a game of chance are significantly different from what many people would naturally assume.

An example is the game of crown and anchor, widely played by British seamen in the eighteenth century. It uses three dice, each bearing not the numbers 1–6 but six symbols: a crown, an anchor, and the four card suits of diamond, spade, club, and heart. These symbols are also marked on a mat. Players bet by placing money on the mat and throwing the three dice. If any of the symbols that they have bet on shows up, the banker pays them their stake, multiplied by the number of dice showing that symbol. For example, if they bet £1 on the crown, and two crowns turn up, they win £2 in addition to their stake; if three crowns turn up, they win £3 in addition to their stake. It all sounds very reasonable, but probability theory tells us that in the long run a player can expect to lose 8% of his stake.

Probability theory began to take off when it attracted the attention of Blaise Pascal. Pascal was the son of a Rouen tax collector and a child prodigy. In 1646 he was converted to Jansenism, a sect of Roman Catholicism that Pope Innocent X deemed heretical in 1655. The year before, Pascal had experienced what he called his ‘second conversion', probably triggered by a near-fatal accident when his horses fell off the edge of Neuilly bridge and his carriage nearly did the same. Most of his output from then on was religious philosophy. But just before the accident, he and Fermat were writing to each other about a mathematical problem to do with gambling. The Chevalier de Meré, a French writer who called himself a knight even though he wasn't, was a friend of Pascal's, and he asked how the stakes in a series of games of chance should be divided if the contest had to be abandoned part way through. This question was not new: it goes back to the Middle Ages. What was new was its solution. In an exchange of letters, Pascal and Fermat found the correct answer. Along the way they created a new branch of mathematics: probability theory.

A central concept in their solution was what we now call ‘expectation'. In a game of chance, this is a player's average return in the long run. It would, for example, be 92 pence for crown and anchor with a £1 stake. After his second conversion, Pascal put his gambling past behind him, but he enlisted its aid in a famous philosophical argument, Pascal's wager.
²
Pascal assumed, playing Devil's advocate, that someone might consider the existence of God to be highly unlikely. In his
Pensées
(‘Thoughts') of 1669, Pascal analysed the consequences from the point of view of probabilities:

Let us weigh the gain and the loss in wagering that God is [exists]. Let us estimate these two chances. If you gain, you gain all; if you lose, you lose nothing. Wager, then, without hesitation that He is. . . There is here an infinity of an infinitely happy life to gain, a chance of gain against a finite number of chances of loss, and what you stake is finite. And so our proposition is of infinite force, when there is the finite to stake in a game where there are equal risks of gain and of loss, and the infinite to gain.

Probability theory arrived as a fully fledged area of mathematics in 1713 when Jacob Bernoulli published his
Ars Conjectandi
(‘Art of Conjecturing'). He started with the usual working definition of the probability of an event: the proportion of occasions on which it will happen, in the long run, nearly all the time. I say ‘working definition' because this approach to probabilities runs into trouble if you try to make it fundamental. For example, suppose that I have a fair coin and keep tossing it. Most of the time I get a random-looking sequence of heads and tails, and if I keep tossing for long enough I will get heads roughly half the time. However, I seldom get heads exactly half the time: this is impossible on odd-numbered tosses, for example. If I try to modify the definition by taking inspiration from calculus, so that the probability of throwing heads is the limit of the proportion of heads as the number of tosses tends to infinity, I have to prove that this limit exists. But sometimes it doesn't. For example, suppose that the sequence of heads and tails goes

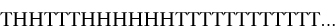
with one tail, two heads, three tails, six heads, twelve tails, and so on – the numbers doubling at each stage after the three tails. After three tosses the proportion of heads is 2/3, after six tosses it is 1/3, after twelve tosses it is back to 2/3, after twenty-four it is 1/3,. . . so the proportion oscillates to and fro, between 2/3 and 1/3, and therefore has no well-defined limit.

Agreed, such a sequence of tosses is very unlikely, but to define ‘unlikely' we need to define probability, which is what the limit is supposed to achieve. So the logic is circular. Moreover, even if the limit exists, it might not be the ‘correct' value of 1/2. An extreme case occurs when the coin always lands heads. Now the limit is 1. Again, this is wildly improbable, but. . .

Bernoulli decided to approach the whole issue from the opposite direction. Start by simply
defining
the probability of heads and tails to be some number
p
between 0 and 1. Say that the coin is fair if
p =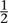
, and biased
if not. Now Bernoulli proves a basic theorem, the law of large numbers. Introduce a reasonable rule for assigning probabilities to a series of repeated events. The law of large numbers states that in the long run, with the exception of a fraction of trials that becomes arbitrarily small, the proportion of heads does have a limit, and that limit is
p
. Philosophically, this theorem shows that by assigning probabilities – that is, numbers – in a natural way, the interpretation ‘proportion of occurrences in the long run, ignoring rare exceptions' is valid. So Bernoulli takes the point of view that the numbers assigned as probabilities provide a consistent mathematical model of the process of tossing a coin over and over again.