In Pursuit of the Unknown (10 page)

This depends on
o
, which is only to be expected since we are averaging the rate of change over a nonzero interval. However, if
o
becomes smaller and smaller, ‘flowing towards' zero, the rate of change
2x + o
gets closer and closer to
2x
. This does not depend on o, and it gives the instantaneous rate of change at
x
.

Leibniz performed essentially the same calculation, replacing
o
by
dx
(‘small difference in
x'
), and defining d
y
to be the corresponding small change in
y
. When a variable
y
depends on another variable
x
, the rate of change of
y
with respect to
x
is called the derivative of
y
. Newton wrote the dy derivative of
y
by placing a dot above it: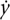
. Leibniz wrote
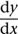. For higher derivatives, Newton used more dots, while Leibniz wrote things like
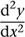. Today we say that
y
is a
function
of
x
and write
y = f(x)
, but this concept existed only in rudimentary form at the time. We either use Leibniz's notation, or a variant of Newton's in which the dot is replaced by a dash, which is easier to print:
y', y”
. We also write
f
'(
x
) and
f
”(
x
) to emphasise that the derivatives are themselves functions. Calculating the derivative is called differentiation.

Integral calculus – finding areas – turns out to be the inverse of differential calculus – finding slopes. To see why, imagine adding a thin slice on the end of the shaded area of
Figure 12
. This slice is very close to a long thin rectangle, of width
o
and height
y
. Its area is therefore very close to
oy
. The rate at which the area changes, with respect to
x
, is the ratio
oy/o
, which equals
y
. So the derivative of the area is the original function. Both Newton and Leibniz understood that the way to calculate the area, a process called integration, is the reverse of differentiation in this sense. Leibniz first wrote the integral using the symbol omn., short for
omnia
, or ‘sum', in Latin. Later he changed this to ∫, an old-fashioned long
s
, also standing for ‘sum'. Newton had no systematic notation for the integral.

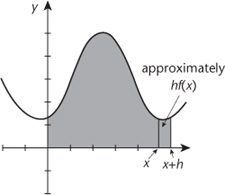
Fig 12
Adding a thin slice to the area beneath the curve
y
=
f
(
x
).

Newton did make one crucial advance, however. Wallis had calculated the derivative of any power
x
^a
: it is
ax
^a
−1
. So the derivatives of
x
³
,
x
⁴
,
x
⁵
are 3
x
²
,
4x
³
, 5
x
⁴
, for example. He had extended this result to any polynomial – a finite combination of powers, such as 3
x
⁷
− 25
x
⁴
+
x
²
− 3. The trick is to consider each power separately, find the corresponding derivatives, and combine them in the same manner. Newton noticed that the same method worked for infinite series, expressions involving infinitely many powers of the variable. This let him perform the operations of calculus on many other expressions, more complicated than polynomials.

Given the close correspondence between the two versions of calculus, differing mainly in unimportant features of the notation, it is easy to see how a priority dispute might have arisen. However, the basic idea is a fairly direct formulation of the underlying question, so it is also easy to see how Newton and Leibniz could have arrived at their versions independently, despite the similarities. In any case, Fermat and Wallis had beaten them both to many of their results. The dispute was pointless.

A more fruitful controversy concerned the logical structure of calculus, or more precisely, the illogical structure of calculus. A leading critic was the Anglo-Irish philosopher George Berkeley, Bishop of Cloyne. Berkeley had a religious agenda; he felt that the materialist view of the world that was developing from Newton's work represented God as a detached creator who stood back from his creation as soon as it got going and thereafter left it to its own devices, quite unlike the personal, immanent God of Christian belief. So he attacked logical inconsistencies in the foundations of calculus, presumably hoping to discredit the resulting science. His attack had no discernible effect on the progress of mathematical physics, for a straightforward reason: the results obtained using calculus shed so much insight into nature, and agreed so well with experiment, that the logical
foundations seemed unimportant. Even today, physicists still take this view: if it works, who cares about logical hair-splitting?

Berkeley argued that it makes no logical sense to maintain that a small quantity (Newton's o, Leibniz's
dx
) is nonzero for most of a calculation, and then to set it to zero, if you have previously divided both the numerator and the denominator of a fraction by that very quantity. Division by zero is not an acceptable operation in arithmetic, because it has no unambiguous meaning. For example, 0 × 1 = 0 × 2, since both are 0, but if we divide both sides of this equation by 0 we get 1 = 2, which is false.
³
Berkeley published his criticisms in 1734 in a pamphlet
The Analyst, a Discourse Addressed to an Infidel Mathematician
.

Newton had, in fact, attempted to sort out the logic, by appealing to a physical analogy. He saw
o
not as a fixed quantity, but as something that
flowed
– varied with time – getting closer and closer to zero without ever actually getting there. The derivative was also defined by a quantity that flowed: the ratio of the change in
y
to that of
x
. This ratio also flowed towards something, but never got there; that something was the instantaneous rate of change – the derivative of
y
with respect to
x
. Berkeley dismissed this idea as the ‘ghost of a departed quantity'.

Leibniz too had a persistent critic, the geometer Bernard Nieuwentijt, who put his criticisms into print in 1694 and 1695. Leibniz had not helped his case by trying to justify his method in terms of ‘infinitesimals', a term open to misinterpretation. However, he did explain that what he meant by this term was not a fixed nonzero quantity that can be arbitrarily small (which makes no logical sense) but a variable nonzero quantity that can
become
arbitrarily small. Newton's and Leibniz's defences were essentially identical. To their opponents, both must have sounded like verbal trickery.

Fortunately, the physicists and mathematicians of the day did not wait for the logical foundations of calculus to be sorted out before they applied it to the frontiers of science. They had an alternative way to make sure they were doing something sensible: comparison with observations and experiments. Newton himself invented calculus for precisely this purpose. He derived laws for how bodies move when a force is applied to them, and combined these with a law for the force exerted by gravity to explain many riddles about the planets and other bodies of the Solar System. His law of gravity is such a pivotal equation in physics and astronomy that it deserves, and gets, a chapter of its own (the next one). His law of motion – strictly, a system of three laws, one of which contained most of the mathematical content – led fairly directly to calculus.

Ironically, when Newton published these laws and their scientific
applications in his
Principia
, he eliminated all traces of calculus and replaced it by classical geometric arguments. He probably thought that geometry would be more acceptable to his intended audience, and if he did, he was almost certainly right. However, many of his geometric proofs are either motivated by calculus, or depend on the use of calculus techniques to determine the correct answers, upon which the strategy of the geometric proof relies. This is especially clear, to modern eyes, in his treatment of what he called ‘generated quantities' in Book II of
Principia
. These are quantities that increase or decrease by ‘continual motion or flux', the fluxions of his unpublished book. Today we would call them continuous (indeed differentiable) functions. In place of explicit operations of the calculus, Newton substituted a geometric method of ‘prime and ultimate ratios'. His opening lemma (the name given to an auxiliary mathematical result that is used repeatedly but has no intrinsic interest in its own right) gives the game away, because it
defines
equality of these flowing quantities like this:

Quantities, and the ratios of quantities, which in any finite time converge continually to equality, and before the end of that time approach nearer to each other than by any given difference, become ultimately equal.

In Never
at Rest
, Newton's biographer Richard Westfall explains how radical and novel this lemma was: ‘Whatever the language, the concept . . . was thoroughly modern; classical geometry had contained nothing like it.'
⁴
Newton's contemporaries must have struggled to figure out what Newton was getting at. Berkeley presumably never did, because – as we will shortly see – it contains the basic idea needed to dispose of his objection.

Calculus, then, was playing an influential role behind the scenes of the
Principia
, but it made no appearance on stage. As soon as calculus peeped out from behind the curtains, however, Newton's intellectual successors quickly reverse-engineered his thought processes. They rephrased his main ideas in the language of calculus, because this provided a more natural and more powerful framework, and set out to conquer the scientific world.