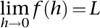In Pursuit of the Unknown (11 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

The clue was already visible in Newton's laws of motion. The question that led Newton to these laws was a philosophical one: what causes a body to move, or to change its state of motion? The classical answer was Aristotle's: a body moves because a force is applied to it, and this affects its
velocity. Aristotle also stated that in order to keep a body moving, the force must continue to be applied. You can test Aristotle's statements by placing a book or similar object on a table. If you push the book, it starts to move, and if you keep pushing with much the same force it continues to slide over the table at a roughly constant velocity. If you stop pushing, the book stops moving. So Aristotle's views seem to agree with experiment. However, the agreement is superficial, because the push is not the only force that acts on the book. There is also friction with the surface of the table. Moreover, the faster the book moves, the greater the friction becomes â at least, while the book's velocity remains reasonably small. When the book is moving steadily across the table, propelled by a steady force, the frictional resistance cancels out the applied force, and the total force acting on the body is actually zero.
Newton, following earlier ideas of Galileo and Descartes, realised this. The resulting theory of motion is very different from Aristotle's. Newton's three laws are:
First law
. Every body continues in its state of rest, or of uniform motion in a right [straight] line, unless it is compelled to change that state by forces impressed upon it.
Second law
. The change of motion is proportional to the motive power impressed, and is made in the direction of the right line in which that force is impressed. (The constant of proportionality is the reciprocal of the body's mass; that is, 1 divided by that mass.)
Third law
. To every action there is always opposed an equal reaction.
The first law explicitly contradicts Aristotle. The third law says that if you push something, it pushes back. The second law is where calculus comes in. By âchange of motion' Newton meant the rate at which the body's velocity changes: its acceleration. This is the derivative of velocity with respect to time, and the second derivative of position. So Newton's second law of motion specifies the relation between a body's position, and the forces that act on it, in the form of a
differential equation:
second derivative of position = force/mass
To find the position itself, we have to solve this equation, deducing the position from its second derivative.
This line of thought leads to a simple explanation of Galileo's observations of a rolling ball. The crucial point is that the acceleration of the ball is
constant
. I stated this previously, using a rough-and-ready
calculation applied at discrete intervals of time; now we can do it properly, allowing time to vary continuously. The constant is related to the force of gravity and the angle of the slope, but here we don't need that much detail. Suppose that the constant acceleration is
a
. Integrating the corresponding function, the velocity down the slope at time
t
is
at
+
b
, where
b
is the velocity at time zero. Integrating again, the position down the slope is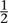 at
at
2
+
bt
+
c
, where
c
is the position at time zero. In the special case
a
= 2,
b = 0, c = 0
the successive positions fit my simplified example: the position at time
t
is
t
2
. A similar analysis recovers Galileo's major result: the path of a projectile is a parabola.
Newton's laws of motion did not just provide a way to calculate how bodies move. They led to deep and general physical principles. Paramount among these are âconservation laws', telling us that when a system of bodies, no matter how complicated, moves, certain features of that system
do not change
. Amid the tumult of the motion, a few things remain serenely unaffected. Three of these conserved quantities are energy, momentum, and angular momentum.
Energy can be defined as the capacity to do work. When a body is raised to a certain height, against the (constant) force of gravity, the work done to put it there is proportional to the body's mass, the force of gravity, and the height to which it is raised. Conversely, if we then let the body go, it can perform the same amount of work when it falls back to its original height. This type of energy is called
potential energy
.
On its own, potential energy would not be terribly interesting, but there is a beautiful mathematical consequence of Newton's second law of motion leading to a second kind of energy:
kinetic energy
. As a body moves, both its potential energy and its kinetic energy change. But the change in one exactly compensates for the change in the other. As the body descends under gravity, it speeds up. Newton's law allows us to calculate how its velocity changes with height. It turns out that the decrease in potential energy is exactly equal to half the mass times the square of the velocity. If we give that quantity a name â kinetic energy â then the total energy, potential plus kinetic, is conserved. This mathematical consequence of Newton's laws proves that perpetual motion machines are impossible: no mechanical device can keep going indefinitely and do work without some external input of energy.
Physically, potential and kinetic energy seem to be two different things; mathematically, we can trade one for the other. It is as if motion
somehow converts potential energy into kinetic. âEnergy', as a term applicable to both, is a convenient abstraction, carefully defined so that it is conserved. As an analogy, travellers can convert pounds into dollars. Currency exchanges have tables of exchange rates, asserting that, say, 1 pound is of equal value to 1.4693 dollars. They also deduct a sum of money for themselves. Subject to technicalities of bank charges and so on, the total monetary value involved in the transaction is supposed to balance out: the traveller gets exactly the amount in dollars that corresponds to their original sum in pounds, minus various deductions. However, there isn't a physical
thing
built into banknotes that somehow gets swapped out of a pound note into a dollar note and some coins. What gets swapped is the human convention that these particular items have monetary value.
Energy is a new kind of âphysical' quantity. From a Newtonian viewpoint, quantities such as position, time, velocity, acceleration, and mass have direct physical interpretations. You can measure position with a ruler, time with a clock, velocity and acceleration using both pieces of apparatus, and mass with a balance. But you don't measure energy using an energy meter. Agreed, you can measure certain specific
types
of energy. Potential energy is proportional to height, so a ruler will suffice if you know the force of gravity. Kinetic energy is half the mass times the square of the velocity: use a balance and a speedometer. But
energy
, as a concept, is not so much a physical thing as a convenient fiction that helps to balance the mechanical books.
Momentum, the second conserved quantity, is a simple concept: mass times velocity. It comes into play when there are several bodies. An important example is a rocket; here one body is the rocket and the other is its fuel. As fuel is expelled by the engine, conservation of momentum implies that the rocket must move in the opposite direction. This is how a rocket works in a vacuum.
Angular momentum is similar, but it relates to spin rather than velocity. It is also central to rocketry, indeed the whole of mechanics, terrestrial or celestial. One of the biggest puzzles about the Moon is its large angular momentum. The current theory is that the Moon was splashed off when a Mars-sized planet hit the Earth about 4.5 billion years ago. This explains the angular momentum, and until recently was generally accepted, but it now seems that the Moon has too much water in its rocks. Such an impact should have boiled a lot of the water away.
5
Whatever the eventual outcome, angular momentum is of central importance here.
Calculus works. It solves problems in physics and geometry, getting the right answers. It even leads to new and fundamental physical concepts like energy and momentum. But that doesn't answer Bishop Berkeley's objection. Calculus has to work as mathematics, not just agree with physics. Both Newton and Leibniz understood that
o
or
dx
cannot be both zero and nonzero. Newton tired to escape from the logical trap by employing the physical image of a fluxion. Leibniz talked of infinitesimals. Both referred to quantities that approach zero without ever getting there â but what are these things? Ironically, Berkeley's gibe about âghosts of departed quantities' comes close to resolving the issue, but what he failed to take account of â and what both Newton and Leibniz emphasised â was
how
the quantities departed. Make them depart in the right way and you can leave a perfectly well-formed ghost. If either Newton or Leibniz had framed their intuition in rigorous mathematical language, Berkeley might have understood what they were getting at.
The central question is one that Newton failed to answer explicitly because it seemed obvious. Recall that in the example where
y
= x
2
, Newton obtained the derivative as 2
x
+
o
, and then asserted that as
o
flows towards zero, 2
x
+ o flows towards 2
x
. This may seem obvious, but we can't set
o
= 0 to prove it. It is true that
we get the right result by doing that
, but this is a red herring.
6
In
Principia
Newton slid round this issue altogether, replacing 2
x
+
o
by his âprime ratio' and 2
x
by his âultimate ratio'. But the real key to progress is to tackle the issue head on. How do we
know
that the closer
o
approaches zero, the closer 2
x
+
o
approaches 2
x
? It may seem a rather pedantic point, but if I'd used more complicated examples the correct answer might not seem so plausible.
When mathematicians returned to the logic of calculus, they realised that this apparently simple question was the heart of the matter. When we say that
o
approaches zero, we mean that given any nonzero positive number,
o
can be chosen to be smaller than that number. (This is obvious: let
o
be half that number, for instance.) Similarly, when we say that 2
x
+
o
approaches 2
x
, we mean that the difference approaches zero, in the previous sense. Since the difference happens to be
o
itself in this case, that's even more obvious: whatever âapproaches zero' means, clearly
o
approaches zero when
o
approaches zero. A more complicated function than the square would require a more complicated analysis.
The answer to this key question is to state the process in formal mathematical terms, avoiding ideas of âflow' altogether. This breakthrough came about through the work of the Bohemian mathematician and theologian Bernard Bolzano and the German mathematician Karl
Weierstrass. Bolzano's work dates from 1816, but it was not appreciated until about 1870 when Weierstrass extended the formulation to complex functions. Their answer to Berkeley was the concept of a limit. I'll state the definition in words and leave the symbolic version to the Notes.
7
Say that a function
f
(
h
) of a variable
h
tends to a limit
L
as
h
tends to zero if, given any positive nonzero number, the difference between
f
(
h
) and
L
can be made smaller than that number by choosing sufficiently small nonzero values of
h
. In symbols,