In Pursuit of the Unknown (7 page)

When Napier started thinking about powers of numbers, in the late sixteenth century, the idea of reducing multiplication to addition was already circulating among mathematicians. A rather complicated method known as ‘prosthapheiresis', based on a formula involving trigonometric functions, was in use in Denmark.
³
Napier, intrigued, was smart enough to
realise that powers of a fixed number could do the same job more simply. The necessary tables didn't exist – but that was easily remedied. Some public-spirited soul must carry out the work. Napier volunteered himself for the task, but he made a strategic error. Instead of using a base that was slightly bigger than 1, he used a base slightly smaller than 1. In consequence, the sequence of powers started out with big numbers, which got successively smaller. This made the calculations slightly more clumsy.

Briggs spotted this problem, and saw how to deal with it: use a base slightly larger than 1. He also spotted a subtler problem, and dealt with that as well. If Napier's method were modified to work with powers of something like 1.0000000001, there would be no straightforward relation between the logarithms of, say, 12.3456 and 1.23456. So it wasn't entirely clear when the table could
stop
. The source of the problem was the value of log 10, because

log 10
x
= log 10 + log
x

Unfortunately log 10 was messy: with the base 1.0000000001 the logarithm of 10 was 23,025,850,929. Briggs thought it would be much nicer if the base could be chosen so that log 10 = 1. Then log 10
x
= 1 + log
x
, so that whatever log 1.23456 might be, you just had to add 1 to it to get log 12.3456. Now tables of logarithms need only run from 1 to 10. If bigger numbers turned up, you just added the appropriate whole number.

To make log 10 = 1, you do what Napier did, using a base of 1.0000000001, but then you divide every logarithm by that curious number 23,025,850,929. The resulting table consists of logarithms to base 10, which I'll write as log
₁₀
x
. They satisfy

log
₁₀
xy
= log
₁₀
x
+ log
₁₀
y

as before, but also

log
₁₀
10
x
= log
₁₀
x
+ 1

Within two years Napier was dead, so Briggs started work on a table of base-10 logarithms. In 1617 he published
Logarithmorum Chilias Prima
(‘Logarithms of the First Chiliad'), the logarithms of the integers from 1 to 1000 accurate to 14 decimal places. In 1624 he followed it up with
Arithmetic Logarithmica
(‘Arithmetic of Logarithms'), a table of base-10 logarithms of numbers from 1 to 20,000 and from 90,000 to 100,000, to the same accuracy. Others rapidly followed Briggs's lead, filling in the large
gap and developing auxiliary tables such as logarithms of trigonometric functions like log sin
x
.

The same ideas that inspired logarithms allow us to define powers
x
^a
of a positive variable
x
for values of
a
that are not positive whole numbers. All we have to do is insist that our definitions must be consistent with the equation
x
^a
x
^b
=
x
^a
+
b
, and follow our noses. To avoid nasty complications, it is best to assume
x
is positive, and to define
x
^a
so that this is also positive. (For negative
x
, it's best to introduce complex numbers, as in
Chapter 5
.)

For example, what is
x
⁰
? Bearing in mind that
x
¹
=
x
, the formula says that
x
⁰
must satisfy
x
⁰
x
=
x
⁰⁺¹
=
x
. Dividing by
x
we find that
x
= 1. Now what about
x
^−1
? Well, the formula says that
x
^−1
x
=
x
^−1+1
=
x
⁰
= 1. Dividing by
x
, we get
x
^−1
= 1/
x
. Similarly
x
^−2
= 1/
x
²
,
x
^−3
= 1/
x
³
, and so on.

It starts to get more interesting, and potentially very useful, when we think about
x
^1/2
. This has to satisfy
x
^1/2
x
^1/2
=
x
^1/2+1/2
=
x
¹
=
x
. So
x
^1/2
, multiplied by itself, is
x
. The only number with this property is the square root of
x
. So
x
^1/2
=
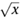. Similarly,
x
^1/3
=
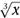, the cube root. Continuing in this manner we can define
x
^p/q
for any fraction
p/q
. Then, using fractions to approximate real numbers, we can define
x
^a
for any real
a
. And the equation
x
^a
x
^b
=
x
^a+b
still holds.

It also follows that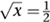 log
log
x
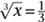, and log
log
x
, so we can calculate square roots and cube roots easily using a table of logarithms. For example, to find the square root of a number we form its logarithm, divide by 2, and then work out which number has the result as its logarithm. For cube roots, do the same but divide by 3. Traditional methods for these problems were tedious and complicated. You can see why Napier showcased square and cube roots in the preface to his book.

As soon as complete tables of logarithms were available, they became an indispensable tool for scientists, engineers, surveyors, and navigators. They saved time, they saved effort, and they increased the likelihood that the answer was correct. Early on, astronomy was a major beneficiary, because astronomers routinely needed to perform long and difficult calculations. The French mathematician and astronomer Pierre Simon de Laplace said that the invention of logarithms ‘reduces to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust'. As the use of machinery in manufacturing grew, engineers started to make more and more use of mathematics – to design complex gears,
analyse the stability of bridges and buildings, and construct cars, lorries, ships, and aeroplanes. Logarithms were a firm part of the school mathematics curriculum a few decades ago. And engineers carried what was in effect an analogue calculator for logarithms in their pockets, a physical representation of the basic equation for logarithms for on-the-spot use. They called it a slide rule, and they used it routinely in applications ranging from architecture to aircraft design.

The first slide rule was constructed by an English mathematician, William Oughtred, in 1630, using circular scales. He modified the design in 1632, by making the two rulers straight. This was the first slide rule. The idea is simple: when you place two rods end to end, their lengths add. If the rods are marked using a logarithmic scale, in which numbers are spaced according to their logarithms, then the corresponding numbers
multiply
. For instance, set the 1 on one rod against the 2 on the other. Then against any number
x
on the first rod, we find
2x
on the second. So opposite 3 we find 6, and so on, see
Figure 11
. If the numbers are more complicated, say 2.67 and 3.51, we place 1 opposite 2.67 and read off whatever is opposite 3.59, namely 9.37. It's just as easy.

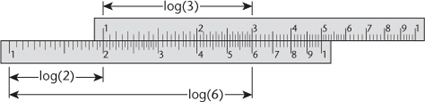
Fig 11
Multiplying 2 by 3 on a slide rule.

Engineers quickly developed fancy slide rules with trigonometric functions, square roots, log-log scales (logarithms of logarithms) to calculate powers, and so on. Eventually logarithms took a back seat to digital computers, but even now the logarithm still plays a huge role in science and technology, alongside its inseparable companion, the exponential function. For base-10 logarithms, this is the function 10
^x
; for natural logarithms, the function e
^x
, where e = 2.71828, approximately. In each pair, the two functions are inverse to each other. If you take a number, form its logarithm, and then form the exponential of that, you get back the number you started with.

Why do we need logarithms now that we have computers?

In 2011 a magnitude 9.0 earthquake just off the east coast of Japan
caused a gigantic tsunami, which devastated a large populated area and killed around 25,000 people. On the coast was a nuclear power plant, Fukushima Dai-ichi (Fukushima number 1 power plant, to distinguish it from a second nuclear power plant situated nearby). It comprised six separate nuclear reactors: three were in operation when the tsunami struck; the other three had temporarily ceased operating and their fuel had been transferred to pools of water outside the reactors but inside the reactor buildings.