In Pursuit of the Unknown (4 page)

Fig 6
Splitting a triangle into two with right angles.

Once in possession of trigonometric functions, it is straightforward to extend Pythagoras's equation to triangles that do not have a right angle.
Figure 6
shows a triangle with an angle
C
and sides
a, b, c
. Split the triangle into two right-angled ones as shown. Then two applications of Pythagoras and some algebra
⁴
prove that

a
²
+
b
²
− 2
ab
cos
C
=
c
²

which is similar to Pythagoras's equation, except for the extra term −2
ab
cos
C
. This ‘cosine rule' does the same job as Pythagoras, relating
c
to
a
and
b
, but now we have to include information about the angle
C
.

The cosine rule is one of the mainstays of trigonometry. If we know two sides of a triangle and the angle between them, we can use it to calculate the third side. Other equations then tell us the remaining angles. All of these equations can ultimately be traced back to right-angled triangles.

Armed with trigonometric equations and suitable measuring apparatus, we can carry out surveys and make accurate maps. This is not a new idea. It appears in the Rhind Papyrus, a collection of ancient Egyptian mathematical techniques dating from 1650
BC.
The Greek philosopher Thales used the geometry of triangles to estimate the heights of the Giza pyramids in about 600
BC.
Hero of Alexandria described the same technique in 50
AD.
Around 240
BC
Greek mathematician, Eratosthenes, calculated the size of the Earth by observing the angle of the Sun at noon in two different places: Alexandria and Syene (now Aswan) in Egypt. A succession of Arabian scholars preserved and developed these methods, applying them in particular to astronomical measurements such as the size of the Earth.

Surveying began to take off in 1533 when the Dutch mapmaker Gemma Frisius explained how to use trigonometry to produce accurate maps, in
Libellus de Locorum Describendorum Ratione
(‘Booklet Concerning a
Way of Describing Places'). Word of the method spread across Europe, reaching the ears of the Danish nobleman and astronomer Tycho Brahe. In 1579 Tycho used it to make an accurate map of Hven, the island where his observatory was located. By 1615 the Dutch mathematician Willebrord Snellius (Snel van Royen) had developed the method into essentially its modern form:
triangulation
. The area being surveyed is covered with a network of triangles. By measuring one initial length very carefully, and many angles, the locations of the corners of the triangle, and hence any interesting features within them, can be calculated. Snellius worked out the distance between two Dutch towns, Alkmaar and Bergen op Zoom, using a network of 33 triangles. He chose these towns because they lay on the same line of longitude and were exactly one degree of arc apart. Knowing the distance between them, he could work out the size of the Earth, which he published in his
Eratosthenes Batavus
(‘The Dutch Eratosthenes') in 1617. His result is accurate to within 4%. He also modified the equations of trigonometry to reflect the spherical nature of the Earth's surface, an important step towards effective navigation.

Triangulation is an indirect method for calculating distances using angles. When surveying a stretch of land, be it a building site or a country, the main practical consideration is that it is much easier to measure angles than it is to measure distances. Triangulation lets us measure a few distances and lots of angles; then everything else follows from the trigonometric equations. The method begins by setting out one line between two points, called the baseline, and measuring its length directly to very high accuracy. Then we choose a prominent point in the landscape that is visible from both ends of the baseline, and measure the angle from the baseline to that point, at both ends of the baseline. Now we have a triangle, and we know one side of it and two angles, which fix its shape and size. We can then use trigonometry to work out the other two sides.

In effect, we now have two more baselines: the newly calculated sides of the triangle. From those, we can measure angles to other, more distant points. Continue this process to create a network of triangles that covers the area being surveyed. Within each triangle, observe the angles to all noteworthy features – church towers, crossroads, and so on. The same trigonometric trick pinpoints their precise locations. As a final twist, the accuracy of the entire survey can be checked by measuring one of the final sides directly.

By the late eighteenth century, triangulation was being employed routinely in surveys. The Ordnance Survey of Great Britain began in 1783, taking 70 years to complete the task. The Great Trigonometric Survey of
India, which among other things mapped the Himalayas and determined the height of Mount Everest, started in 1801. In the twenty-first century, most large-scale surveying is done using satellite photographs and GPS (the Global Positioning System). Explicit triangulation is no longer employed. But it is still there, behind the scenes, in the methods used to deduce locations from the satellite data.

Pythagoras's theorem was also vital to the invention of coordinate geometry. This is a way to represent geometric figures in terms of numbers, using a system of lines, known as axes, labelled with numbers. The most familiar version is known as Cartesian coordinates in the plane, in honour of the French mathematician and philosopher René Descartes, who was one of the great pioneers in this area – though not the first. Draw two lines: a horizontal one labelled
x
and a vertical one labelled
y
. These lines are known as axes (plural of axis), and they cross at a point called the origin. Mark points along these two axes according to their distance from the origin, like the markings on a ruler: positive numbers to the right and up, negative to the left and down. Now we can determine any point in the plane in terms of two numbers
x
and
y
, its coordinates, by connecting the point to the two axes as in
Figure 7
. The pair of numbers (
x
,
y
) completely specifies the location of the point.

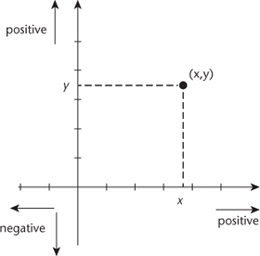
Fig 7
The two axes and the coordinates of a point.

The great mathematicians of seventeenth-century Europe realised that, in this context, a line or curve in the plane corresponds to the set of solutions (
x
,
y
) of some equation in
x
and
y
. For instance,
y
=
x
determines a
diagonal line sloping from lower left to top right, because (
x
,
y
) lies on that line if and only if
y
=
x
. In general, a linear equation – of the form
ax
+
by
=
c
for constants
a
,
b
,
c
– corresponds to a straight line, and vice versa.

What equation corresponds to a circle? This is where Pythagoras's equation comes in. It implies that the distance
r
from the origin to the point (
x
,
y
) satisfies

r
²
=
x
²
+
y
²

and we can solve this for
r
to obtain

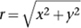
Since the set of all points that lie at distance
r
from the origin is a circle of radius
r
, whose centre is the origin, so the same equation defines a circle. More generally, the circle of radius
r
with centre at (
a
,
b
) corresponds to the equation

(
x
−
a
)
²
+ (
y
−
b
)
²
=
r
²

and the same equation determines the distance
r
between the two points (
a
,
b
) and (
x
,
y
). So Pythagoras's theorem tells us two vital things: which equations yield circles, and how to calculate distances from coordinates.

Pythagoras's theorem, then, is important in its own right, but it exerts even more influence through its generalisations. Here I will pursue just one strand of these later developments to bring out the connection with relativity, to which we return in
Chapter 13
.

The proof of Pythagoras's theorem in Euclid's
Elements
places the theorem firmly within the realm of Euclidean geometry. There was a time when that phrase could have been replaced by just ‘geometry', because it was generally assumed that Euclid's geometry was the true geometry of physical space. It was obvious. Like most things assumed to be obvious, it turned out to be false.

Euclid derived all of his theorems from a small number of basic assumptions, which he classified as definitions, axioms, and common notions. His set-up was elegant, intuitive, and concise, with one glaring exception, his fifth axiom: ‘If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are
the angles less than the two right angles.' It's a bit of a mouthful:
Figure 8
may help.

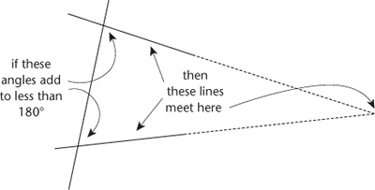
Fig 8
Euclid's parallel axiom.

For well over a thousand years, mathematicians tried to repair what they saw as a flaw. They weren't just looking for something simpler and more intuitive that would achieve the same end, although several of them found such things. They wanted to get rid of the awkward axiom altogether, by proving it. After several centuries, mathematicians finally realised that there were alternative ‘non-Euclidean' geometries, implying that no such proof existed. These new geometries were just as logically consistent as Euclid's, and they obeyed all of his axioms except the parallel axiom. They could be interpreted as the geometry of geodesics – shortest paths – on curved surfaces,
Figure 9
. This focused attention on the meaning of curvature.