In Pursuit of the Unknown (15 page)

It is much the same with spacecraft. The combined gravitational fields of the Sun, planets, and other bodies of the Solar System provide potential energy. The speed of the spacecraft corresponds to kinetic energy. And its motive power – be it rocket fuel, ions, or light-pressure – adds a further energy source, which can be switched on or off as required. The path followed by the spacecraft is a kind of contour line in the corresponding energy landscape, and along that path the total energy remains constant. And some types of contour line are surrounded by tubes, corresponding to nearby energy levels.

Those Victorian railway engineers were also aware that the terrestrial landscape has special features – peaks, valleys, mountain passes – which have a big effect on efficient routes for railway lines, because they constitute a kind of skeleton for the overall geometry of the contours. For instance, near a peak or a valley bottom the contours form closed curves. At peaks, potential energy is locally at a maximum; in a valley, it is at a local minimum. Passes combine features of both, being at a maximum in one direction, but a minimum in another. Similarly, the energy landscape of the Solar System has special features. The most obvious are the planets and moons themselves, which sit at the bottom of gravity wells, like valleys. Equally important, but less visible, are the peaks and passes of the
energy landscape. All these features organise the overall geometry, and with it, the tubes.

The energy landscape has other attractive features for the tourist, notably Lagrange points. Imagine a system consisting only of the Earth and the Moon. In 1772 Joseph-Louis Lagrange discovered that at any instant there are precisely five places where the gravitational fields of the two bodies, together with centrifugal force, cancel out exactly. Three are in line with both Earth and Moon – L1 lies between them, L2 is on the far side of the Moon, and L3 is on the far side of the Earth. The Swiss mathematician Leonhard Euler had already discovered these around 1750. But there are also L4 and L5, known as Trojan points, which lie in the same orbit as the Moon but 60 degrees ahead of it or behind it. As the Moon rotates round the Earth, the Lagrange points rotate with it. Other pairs of bodies also have Lagrange points – Earth/Sun, Jupiter/Sun, Titan/Saturn.

The old-fashioned Hohmann transfer orbit is built from pieces of circles and ellipses, which are the natural trajectories for two-body systems. The new tube-based paths are built from pieces of the natural trajectories of three-body systems, such as Sun/Earth/spacecraft. Lagrange points play a special role, just as peaks and passes did for railways: they are the junctions where tubes meet. L1 is a great place to make small course changes, because the natural dynamics of a spacecraft near L1 is chaotic,
Figure 16
. Chaos has a useful feature (see
Chapter 16
): very small changes in position or speed can create large changes to the trajectory. So it is easy to redirect the spacecraft in a fuel-efficient, though possibly slow, manner.

The first person to take this idea seriously was the German-born mathematician Edward Belbruno, an orbital analyst at the Jet Propulsion Laboratory from 1985 to 1990. He realised that chaotic dynamics in many-body systems provided an opportunity for novel low-energy transfer orbits, naming the technique fuzzy boundary theory. In 1991 he put his ideas into practice. Hiten, a Japanese probe, had been surveying the Moon, and had completed its intended mission, returning to orbit the Earth. Belbruno designed a new orbit that would take it back to the Moon despite having pretty much run out of fuel. After approaching the Moon as intended, Hiten visited its L4 and L5 points to search for cosmic dust that might have been trapped there.

A similar trick was used in 1985 to redirect the almost-dead International Sun–Earth Explorer ISEE-3 to rendezvous with comet Giacobini–Zinner, and it was used again for NASA's Genesis mission to bring back samples of the solar wind. Mathematicians and engineers
wanted to repeat the trick, and to find others of the same kind, which meant finding out what really made it work. It turned out to be tubes.

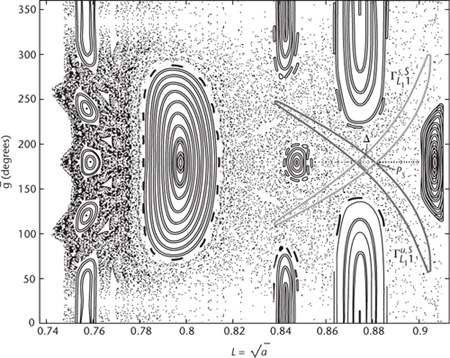
Fig 16
Chaos near Jupiter. The diagram shows a cross-section of orbits. The nested loops are quasiperiodic orbits and the remaining stippled region is a chaotic orbit. The two thin loops crossing each other at the right are cross-sections of tubes.

The underlying idea is simple but clever. Those special places in the energy landscape that resemble mountain passes create bottlenecks that would-be travellers cannot easily avoid. Ancient humans discovered, the hard way, that even though it takes energy to climb a pass, it takes
more
energy to follow any other route – unless you can go round the mountain in a totally different direction. The pass makes the best of a bad choice.

In the energy landscape, the analogues of passes include Lagrange points. Associated with them are very specific inbound paths, which are like the most efficient way to climb up the pass. There are also equally specific outbound paths, analogous to the natural routes down from the pass. To follow these inbound and outbound paths exactly, you have to travel at just the right speed, but if your speed is slightly different you can still stay near those paths. In the late 1960s American mathematicians Charles Conley and Richard McGehee followed up Belbruno's pioneering work, pointing out that each such path is surrounded by a nested set of tubes, one inside the other. Each tube corresponds to a particular choice of speed; the further away it is from the optimal speed, the wider the tube is.
On the surface of any given tube, the total energy is constant, but the constants differ from one tube to another. Much as a contour line is at a constant height, but that height is different for each contour.

 

The way to plan an efficient mission profile, then, is to work out which tubes are relevant to your choice of destination. Then you route your spacecraft along the inside of the first inbound tube, and when it gets to the associated Lagrange point you fire a quick burst on the motors to redirect it along the most suitable outbound tube,
Figure 17
. That tube naturally flows into the corresponding inbound tube of the next switching point. . . and so it goes.

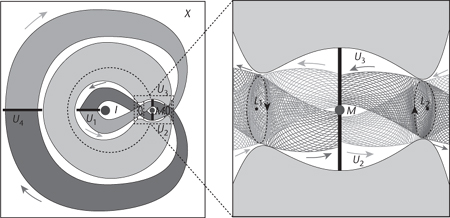
Fig 17
Left
: Tubes meeting near Jupiter.
right
: Close-up of region where the tubes join.

Plans for future tubular missions are already being drawn up. In 2000 Wang Sang Koon, Martin Lo, Jerrold Marsden, and Shane Ross used the tube technique to find a ‘Petit Grand Tour' of the moons of Jupiter, ending with a capture orbit round Europa, which was very tricky with previous methods. The path involves a gravitational boost near Ganymede followed by a tube trip to Europa. A more complex route, requiring even less energy, includes Callisto as well. It makes use of another feature of the energy landscape – resonances. These occur when, say, two moons repeatedly return to the same relative positions, but one revolves twice round Jupiter while the other revolves three times. Any small numbers can replace 2 and 3 here. This route uses five-body dynamics: Jupiter, the three moons, and the spacecraft.

In 2005, Michael Dellnitz, Oliver Junge, Marcus Post, and Bianca Thiere
used tubes to plan an energy-efficient mission from the Earth to Venus. The main tube here links the Sun/Earth L1 point to the Sun/Venus L2 point. As a comparison, this route uses only one third of the fuel required by the European Space Agency's Venus Express mission, because it can use low-thrust engines; the price paid is a lengthening of the transit time from 150 days to about 650 days.

The influence of tubes may go further. In unpublished work, Dellnitz has discovered evidence of a natural system of tubes connecting Jupiter to each of the inner planets. This remarkable structure, now called the Interplanetary Superhighway, hints that Jupiter, long known to be the dominant planet of the Solar System, also plays the role of a celestial Grand Central Station. Its tubes may well have organised the formation of the entire Solar System, determining the spacings of the inner planets.

Why were the tubes not spotted sooner? Until very recently, two vital things were missing. One was powerful computers, capable of carrying out the necessary many-body calculations. They are far too cumbersome by hand. But the other, even more important, was a deep mathematical understanding of the geography of the energy landscape. Without this imaginative triumph of modern mathematical methods, there would be nothing for the computers to calculate. And without Newton's law of gravity, the mathematical methods would never have been devised.

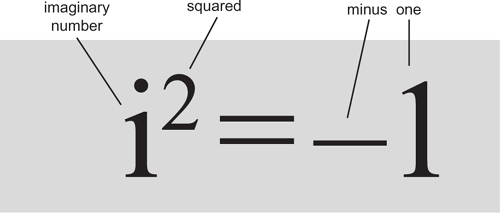
Even though it ought to be impossible, the square of the number i is minus one.

It led to the creation of complex numbers, which in turn led to complex analysis, one of the most powerful areas of mathematics.

Improved methods to calculate trigonometric tables. Generalisations of almost all mathematics to the complex realm. More powerful methods to understand waves, heat, electricity, and magnetism. The mathematical basis of quantum mechanics.

R
enaissance Italy was a hotbed of politics and violence. The north of the country was controlled by a dozen warring city-states, among them Milan, Florence, Pisa, Genoa, and Venice. In the south, Guelphs and Gibellines were in conflict as Popes and Holy Roman Emperors battled for supremacy. Bands of mercenaries roamed the land, villages were laid waste, coastal cities waged naval warfare against each other. In 1454 Milan, Naples, and Florence signed the Treaty of Lodi, and peace reigned for the next four decades, but the papacy remained embroiled in corrupt politics. This was the time of the Borgias, notorious for poisoning anyone who got in the way of their quest for political and religious power, but it was also the time of Leonardo da Vinci, Brunelleschi, Piero della Francesca, Titian, and Tintoretto. Against a backdrop of intrigue and murder, long-held assumptions were coming into question. Great art and great science flourished in symbiosis, each feeding off the other.

Great mathematics flourished as well. In 1545 the gambling scholar Girolamo Cardano was writing an algebra text, and he encountered a new kind of number, one so baffling that he declared it ‘as subtle as it is useless' and dismissed the notion. Rafael Bombelli had a solid grasp of Cardano's algebra book, but he found the exposition confusing, and decided he could do better. By 1572 he had noticed something intriguing: although these baffling new numbers made no sense, they could be used in algebraic calculations and led to results that were demonstrably correct.