In Pursuit of the Unknown (30 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Fig 38
Beats.
Mathematicians first derived the wave equation in the simplest setting they could think of: a vibrating line, a one-dimensional system. Realistic applications required a more general theory, modelling waves in two and three dimensions. Even staying within music, a drum requires two dimensions to model the patterns in which the drumskin vibrates. The same goes for water waves on the surface of the ocean. When an earthquake strikes, the whole Earth rings like a bell, and our planet is three-dimensional. Many other areas of physics involve models with two or three dimensions. Extending the wave equation to higher dimensions turned out to be straightforward; all you had to do was repeat the same kinds of calculation that had worked for the violin string. Having learned to play the game in this simple setting, it wasn't hard to play it for real.
In three dimensions, for example, we use three space coordinates (
x
,
y
,
z
) and time
t
. The wave is described by a function
u
that depends on these four coordinates. For instance, this might describe the pressure in a body of air as sound waves pass through it. Making the same assumptions
as d'Alembert, in particular that the amplitude of the disturbance is small, the same approach leads to an equally pretty equation:
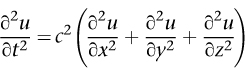
The formula inside the brackets is called the Laplacian, and it corresponds to the average difference between the value of
u
at the point in question, and its value nearby. This expression arises so often in mathematical physics that it has its own special symbol: â
2
u
. To get the Laplacian in two dimensions, we just omit the term involving
z
, leading to the wave equation in that setting.
The main novelty in higher dimensions is that the shape within which the waves arise, called the domain of the equation, can be complicated. In one dimension the only connected shape is an interval, a segment of the line. In two dimensions, however, it can be any shape you can draw in the plane, and in three dimensions, any shape in space. You can model a square drum, a rectangular drum, a circular drum,
4
or a drum shaped like the silhouette of a cat. For earthquakes, you might employ a spherical domain, or for greater accuracy, an ellipsoid squashed slightly at the poles. If you are designing a car and want to eliminate unwanted vibrations, your domain should be car-shaped â or whatever part of the car the engineers want to focus on.
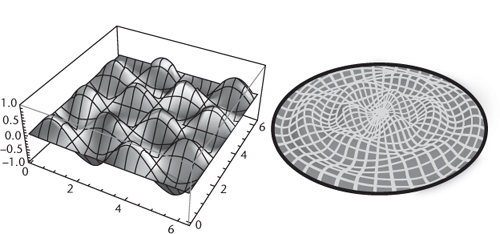
Fig 39
Left
: Snapshot of one mode of a vibrating rectangular drum, with wave numbers 2 and 3.
right
: Snapshot of one mode of a vibrating circular drum.
For any chosen shape of domain, there are functions analogous to Bernoulli's sines and cosines: the simplest patterns of vibration. These
patterns are called modes, or normal modes if you want to make it absolutely clear what you're talking about. All other waves can be obtained by superposing normal modes, again using an infinite series if necessary. The frequencies of the normal modes represent the natural vibrational frequencies of the domain. If the domain is a rectangle, these are trigonometric functions of the form sin
mx
cos
ny
, for integers
m
and
n
, producing waves shaped like
Figure 39
(
left
). If it is a circle, they are determined by new functions, called Bessel functions, with more interesting shapes,
Figure 39
(
right
). The resulting mathematics applies not only to drums, but to water waves, sound waves, electromagnetic waves such as light (
Chapter 11
), even quantum waves (
Chapter 14
). It is fundamental to all of these areas. The Laplacian also turns up in equations for other physical phenomena; in particular, electric, magnetic, and gravitational fields. The mathematician's favourite trick of starting with a toy problem, one so simple that it cannot possibly be realistic, pays off big time for waves.
This is one reason why it is unwise to judge a mathematical idea by the context in which it first arises. Modelling a violin string may seem pointless when what you want to understand is earthquakes. But if you jump in at the deep end, and try to cope with all of the complexities of real earthquakes, you'll drown. You should start out paddling in the shallow end and gain confidence to swim a few lengths of the pool. Then you'll be ready for the high diving board.
The wave equation was a spectacular success, and in some areas of physics it describes reality very closely. However, its derivation requires several simplifying assumptions. When those assumptions are unrealistic, the same physical ideas can be modified to suit the context, leading to different versions of the wave equation.
Earthquakes are a typical example. Here the main problem is not d'Alembert's assumption that the amplitude of the wave is small, but changes in the physical properties of the domain. These properties can have a strong effect on seismic waves, vibrations that travel through the Earth. By understanding those effects, we can look deep inside our planet and find out what it is made of.
There are two main kinds of seismic wave: pressure waves and shear waves, usually abbreviated to P-waves and S-waves. (There are many others: this is a simplified account, covering some of the basics.) Both can occur in a solid medium, but S-waves don't occur in fluids. P-waves are waves of
pressure, analogous to sound waves in air, and the changes in pressure point in the direction along which the wave propagates. Such waves are said to be longitudinal. S-waves are transverse waves, changing at right angles to the direction of travel, like the waves on a violin string. They cause solids to shear, that is, deform like a pack of cards pushed sideways, so that the cards slide along one another. Fluids don't behave like packs of cards.
When an earthquake happens, it sends out both kinds of wave. The P-waves travel faster, so a seismologist somewhere else on the Earth's surface observes those first. Then the slower S-waves arrive. In 1906 the English geologist Richard Oldham exploited this difference to make a major discovery about our planet's interior. Roughly speaking, the Earth has an iron core, surrounded by a rocky mantle, and the continents float on top of the mantle. Oldham suggested that the outer layers of the core must be liquid. If so, S-waves can't pass through those regions, but P-waves can. So there is a kind of S-wave shadow, and you can work out where it is by observing signals from earthquakes. The English mathematician Harold Jeffreys sorted out the details in 1926 and confirmed that Oldham was right.
If the earthquake is big enough, it can cause the entire planet to vibrate in one of its normal modes â the analogues for the Earth of sines and cosines for a violin. The whole planet rings like a bell, in a sense that would be literal if only we could hear the very low frequencies involved. Instruments sensitive enough to record these modes appeared in the 1960s, and they were used to observe the two most powerful earthquakes yet recorded scientifically. These were the Chilean earthquake of 1960 (magnitude 9.5) and the Alaskan earthquake of 1964 (magnitude 9.2). The first killed around 5000 people; the second killed about 130 thanks to its remote location. Both caused tsunamis and did a huge amount of damage. Both offered an unprecedented view of the Earth's deep interior, by exciting the Earth's basic vibrational modes.
Sophisticated versions of the wave equation have given seismologists the ability to see what's happening hundreds of kilometres beneath our feet. They can map the Earth's tectonic plates as one slides beneath another, known as subduction. Subduction causes earthquakes, especially so-called megathrust earthquakes like the two just mentioned. It also gives rise to mountain chains along the edges of continents, such as the Andes, and volcanoes, where the plate gets so deep that it starts to melt and magma rises to the surface. A recent discovery is that the plates need not
subduct as a whole, but can break up into gigantic slabs, sinking back into the mantle at different depths.
The biggest prize in this area would be a reliable way to predict earthquakes and volcanic eruptions. This is proving elusive, because the conditions that trigger such events are complex combinations of many factors in many locations. However, some progress is being made, and the seismologists' version of the wave equation underpins many of the methods being investigated.
The same equations have more commercial applications. Oil companies prospect for liquid gold, a few kilometres underground, by setting off explosions at the surface and using returning echoes from the seismic waves they generate to map out the underlying geology. The main mathematical problem here is to reconstruct the geology from the signals received, which is a bit like using the wave equation backwards. Instead of solving the equation in a known domain to work out what the waves do, mathematicians use the observed wave patterns to reconstruct the geological features of the domain. As is often the case, working backwards like this â solving the inverse problem, in the jargon â is harder than going the other way. But practical methods exist. One of the major oil companies performs such calculations a quarter of a million times every day.
Drilling for oil has its own problems, as the blowout at the Deepwater Horizon oil rig in 2010 made clear. But at the moment, human society is heavily dependent on oil, and it would take decades to reduce this significantly, even if everyone wanted to. Next time you fill up your tank, give a thought to the mathematical pioneers who wanted to know how a violin produces its sounds. It wasn't a practical problem then, and it still isn't today. But without their discoveries, your car would take you nowhere.
| 9 | Ripples and blips |

