In Pursuit of the Unknown (37 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Not content with this initial attempt, he went on to include not just magnetism, but its relation to electricity. As the electrical fluid flowed, it affected the magnetic one, and vice versa. For magnetic fields Maxwell used the mental image of tiny vortices spinning in space. Electric fields were similarly composed of tiny charged spheres. Following this analogy and the resulting mathematics, Maxwell began to understand how a change in the electric force could create a magnetic field. As the spheres of electricity move, they cause the magnetic vortices to spin, like a football fan passing through a turnstile. The fan moves without spinning; the turnstile spins without moving.
Maxwell was slightly dissatisfied with this analogy, saying âI do not
bring it forward. . . as a mode of connection existing in nature. . . It is, however. . . mechanically conceivable and easily investigated, and it serves to bring out the actual mechanical connections between the known electromagnetic phenomena.' To show what he meant, he used the model to explain why parallel wires carrying opposite electrical currents repel each other, and he also explained Faraday's crucial discovery of electromagnetic induction.
The next step was to retain the mathematics while getting rid of the mechanical gadgetry that propelled the analogy. This amounted to writing down equations for the basic interactions between the electrical and magnetic fields, derived from the mechanical model, but divorced from this origin. Maxwell achieved this goal in 1864 in his famous paper âA dynamical theory of the electromagnetic field'.
We now interpret his equations using vectors, which are quantities that possess not just a size, but a direction. The most familiar is velocity: the size is the speed, how fast the object is moving; the direction is the one along which it moves. The direction really does matter: a body moving vertically upwards at 10 kps behaves very differently from one moving vertically downwards at 10 kps. Mathematically, a vector is represented by its three components: its effect along three axes at right angles to each other, such as north/south, east/west, and up/down. The bare bones are thus that a vector is a triple (
x
,
y
,
z
) composed of three numbers,
Figure 44
. The velocity of a fluid at a given point, for instance, is a vector. In contrast, the pressure at a given point is a single number: the fancy term used to distinguish this from a vector is âscalar'.
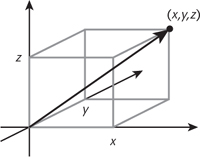
Fig 44
A three-dimensional vector.
In these terms, what is the electric field? From Faraday's perspective it is determined by lines of electrical force. In Maxwell's analogy, these are flow-lines of the electrical fluid. A flow-line tells us in which direction the fluid is flowing, and as a molecule moves along the flow-line, we can also
observe its speed. For each point in space, the flow-line passing through that point therefore determines a vector, which describes the speed and direction of the electric fluid, that is, the strength and direction of the electric field
at that point
. Conversely, if we know these speeds and directions, for every point in space, we can deduce what the flow-lines look like, so in principle we know the electric field.
In short: the electric field is a system of vectors, one for each point in space. Each vector prescribes the strength and direction of the electrical force (exerted on a tiny charged test particle) at that point. Mathematicians call such a quantity a vector field: it is a function that assigns to each point in space the corresponding vector. Similarly, the magnetic field is determined by the magnetic lines of force; it is the vector field corresponding to the forces that would be exerted on a tiny magnetic test particle.
Having sorted out what electric and magnetic fields were, Maxwell could write down equations describing what they did. We now express these equations using two vector operators, known as divergence and curl. Maxwell used specific formulas involving the three components of the electric and magnetic fields. In the special case in which there are no conducting wires or metal plates, no magnets, and everything happens in a vacuum, the equations take a slightly simpler form, and I will restrict the discussion to this case.
Two of the equations tell us that the electric and magnetic fluids are incompressible â that is, electricity and magnetism cannot just leak away, they have to
go
somewhere. This translates as âthe divergence is zero', leading to the equations
â ·
E
= 0     â ·
H
= 0
where the upside-down triangle and the dot are the notation for the divergence. Two more equations tell us that when a region of electric field spins in a small circle, it creates a magnetic field at right angles to the plane of that circle, and similarly a spinning region of magnetic field creates an electric field at right angles to the plane of that circle. There is a curious twist: the electric and magnetic fields point in opposite directions for a given direction of spin. The equations are

where now the upside-down triangle and the cross are the notation for the curl. The symbol
t
stands for time, and
â/ât
is the rate of change with
respect to time. Notice that the first equation has a minus sign, but the second does not: this represents the opposite orientations that I mentioned.
What is
c
? It is a constant, the ratio of electromagnetic to electrostatic units. Experimentally this ratio is just under 300,000, in units of kilometres divided by seconds. Maxwell immediately recognised this number: it is the speed of light in a vacuum. Why did that quantity appear? He decided to find out. One clue, dating back to Newton, and developed by others, was the discovery that light was some kind of wave. But no one knew what the wave consisted of.
A simple calculation provided the answer. Once you know the equations for electromagnetism, you can solve them to predict how the electric and magnetic fields behave in different circumstances. You can also derive general mathematical consequences. For instance, the second pair of equations relates
E
to
H;
any mathematician will immediately try to derive equations that contain only
E
and only
H,
because that lets us concentrate on each field separately. Considering its epic consequences, this task turns out to be absurdly simple â if you have some familiarity with vector calculus. I've put the detailed working in the Notes,
2
but here's a quick summary. Following our noses, we start with the third equation, which relates the curl of
E
to the time-derivative of
H.
We don't have any other equations involving the time-derivative of
H,
but we do have one that involves the curl of
H,
namely, the fourth equation. This suggests that we should take the third equation and form the curl of both sides. Then we apply the fourth equation, simplify, and emerge with

which is the wave equation
!
The same trick applied to the curl of
H
produces the same equation with
H
in place of
E.
(The minus sign is applied twice, so it disappears.) So both the electric and magnetic fields, in a vacuum, obey the wave equation. Since the same constant
c
occurs in each wave equation, they both travel at the same speed, namely
c
. So this little calculation predicts that both the electric field and the magnetic field can simultaneously support a wave â making it an electromagnetic wave, in which both fields vary in concert with each other. And the speed of that wave is . . . the speed of light.
It's another of those trick questions. What travels at the speed of light? This time the answer is what you'd expect: light. But there is a momentous implication:
light is an electromagnetic wave
.
This was stupendous news. There was no reason, prior to Maxwell's derivation of his equations, to imagine such a fundamental link between light, electricity, and magnetism. But there was more. Light comes in many different colours, and once you know that light is a wave, you can work out that these correspond to waves with different wavelengths â distance betweens successive peaks. The wave equation imposes no conditions on the wavelength, so it can be anything. The wavelengths of visible light are restricted to a small range, because of the chemistry of the eye's light-detecting pigments. Physicists already knew of âinvisible light', ultraviolet and infrared. Those, of course, had wavelengths just outside the visible range. Now Maxwell's equations led to a dramatic prediction: electromagnetic waves with other wavelengths should also exist. Conceivably, any wavelength â long or short â could occur,
Figure 45
.
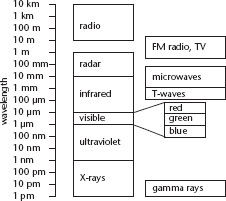
Fig 45
The electromagnetic spectrum.
No one had expected this, but as soon as theory said it ought to happen, experimentalists could go and look for it. One of them was a German, Heinrich Hertz. In 1886 he constructed a device that could generate radio waves and another that could receive them. The transmitter was little more than a machine that could produce a high-voltage spark; theory indicated that such a spark would emit radio waves. The receiver was a circular loop of copper wire, whose size was chosen to resonate with the incoming waves. A small gap in the loop, a few hundredths of a millimetre across, would reveal those waves by producing tiny sparks. In
1887 Hertz did the experiment, and it was a success. He went on to investigate many different features of radio waves. He also measured their speed, getting an answer close to the speed of light, which confirmed Maxwell's prediction and confirmed that his apparatus really was detecting electromagnetic waves.
