In Pursuit of the Unknown (56 page)

I said at the start of this chapter that you don't have anything chaotic in your kitchen, except perhaps that dishwasher. I lied. You probably have several chaotic gadgets: a food processor, an egg-beater. The blade of the food processor follows a very simple rule: go round and round, fast. The food interacts with the blade: it ought to do something simple too. But it doesn't go round and round: it gets mixed up. As the blade cuts through the food, some bits go one side of it, some go the other side: locally, the food gets pulled apart. But it doesn't escape from the mixing bowl, so it all gets folded back in on itself.

Smale and Arnold realised that all chaotic dynamics is like this. They didn't phrase their results in quite that language, mind you: ‘pulled apart' was ‘positive Liapunov exponent' and ‘folded back' was ‘the system has a compact domain'. But in fancy language, they were saying that chaos is like mixing dough.

This also explains something else, noticed especially by Lorenz in 1963. Chaotic dynamics is sensitive to initial conditions. However close the two raisins are to begin with, they eventually get pulled so far apart that their subsequent movements are independent. This phenomenon is often called the butterfly effect: a butterfly flaps its wings, and a month later the weather is completely different from what it would otherwise have been. The phrase is generally credited to Lorenz. He didn't introduce it, but something similar featured in the title of one of his lectures. However, someone else invented the title for him, and the lecture wasn't about the famous 1963 article, but a lesser-known one from the same year.

Whatever the phenomenon is called, it has an important practical consequence. Although chaotic dynamics is in principle deterministic, in practice it becomes unpredictable very quickly, because any uncertainty in the exact initial state grows exponentially fast. There is a prediction horizon beyond which the future cannot be foreseen. For weather, a familiar system whose standard computer models are known to be chaotic, this horizon is a few days ahead. For the Solar System, it is tens of millions of years ahead. For simple laboratory toys, such as a double pendulum (a
pendulum hung from the bottom of another one) it is a few seconds ahead. The long-held assumption that ‘deterministic' and ‘predictable' are the same is wrong. It would be valid if the present state of a system could be measured with perfect accuracy, but that's not possible.

The short-term predictability of chaos can be used to distinguish it from pure randomness. Many different techniques have been devised to make this distinction, and to work out the underlying dynamics if the system is behaving deterministically but chaotically.

Chaos now has applications in every branch of science, from astronomy to zoology. In
Chapter 4
we saw how it is leading to new, more efficient trajectories for space missions. In broader terms, astronomers Jack Wisdom and Jacques Laskar have shown that the dynamics of the Solar System is chaotic. If you want to know whereabouts in its orbit Pluto will be in 10,000,000
AD
– forget it. They have also shown that the Moon's tides stabilise the Earth against influences that would otherwise lead to chaotic motion, causing rapid shifts of climate from warm periods to ice ages and back again. So chaos theory demonstrates that, without the Moon, the Earth would be a pretty unpleasant place to live. This feature of our planetary neighbourhood is often used to argue that the evolution of life on a planet requires a stabilising Moon, but this is an overstatement. Life in the oceans would scarcely notice if the planet's axis changed over a period of millions of years. Life on land would have plenty of time to migrate elsewhere, unless it got trapped somewhere that lacked a land route to a place where conditions were more suitable. Climate change is happening much faster right now than anything that a change in axial tilt could cause.

May's suggestion that irregular population dynamics in an ecosystem might sometimes be caused by internal chaos, rather than extraneous randomness, has been verified in laboratory versions of several real-world ecosystems. In 1995 a team headed by American ecologist James Cushing found chaotic dynamics in populations of the flour beetle (or bran bug)
Tribolium castaneum
, which can infest stores of flour.
²
In 1999, Dutch biologists Jef Huisman and Franz Weissing applied chaos to the ‘paradox of the plankton', the unexpected diversity of plankton species.
³
A standard principle in ecology, the principle of competitive exclusion, states that an ecosystem cannot contain more species than the number of environmental niches, ways to make a living. Plankton appear to violate this principle: the number of niches is small, but the number of species is in the thousands.
They traced this to a loophole in the derivation of the principle of competitive exclusion: the assumption that populations are steady. If the populations can change over time, then the mathematical derivation from the usual model fails, and intuitively different species can occupy the same niche by taking turns – not by conscious cooperation, but by one species temporarily taking over from another and undergoing a population boom, while the displaced species drops to a small population,
Figure 59
.

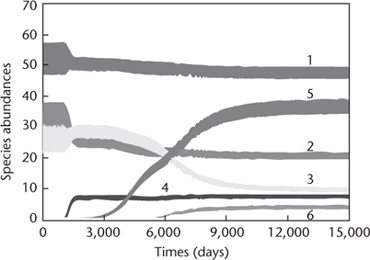
Fig 59
Six species sharing three resources. The bands are closely spaced chaotic oscillations. Courtesy of Jef Huisman and Franz Weissing.

In 2008, Huisman's team published the results of a laboratory experiment with a miniature ecology based on one found in the Baltic Sea, involving bacteria and several kinds of plankton. A six-year study revealed chaotic dynamics in which populations fluctuated wildly, often becoming 100 times as large for a time and then crashing. The usual methods for detecting chaos confirmed its presence. There was even a butterfly effect: the system's prediction horizon was a few weeks.
⁴

There are applications of chaos that impinge on everyday life, but they mostly occur in manufacturing processes and public services, rather than being incorporated into gadgets. The discovery of the butterfly effect has changed the way weather forecasts are carried out. Instead of putting all of the computational effort into refining a single prediction, meteorologists now run many forecasts, making different tiny random changes to the observations provided by weather balloons and satellites before starting each run. If all of these forecasts agree, then the prediction is likely to be accurate; if they differ significantly, the weather is in a less predictable
State. The forecasts themselves have been improved by several other advances, notably in calculating the influence of the oceans on the state of the atmosphere, but the main role of chaos has been to warn forecasters not to expect too much and to quantify how likely a forecast is to be correct.

Industrial applications include a better understanding of mixing processes, which are widely used to make medicinal pills or mix food ingredients. The active medicine in a pill usually occurs in very small quantities, and it has to be mixed with some inert substance. It's important to get enough of the active ingredient in each pill, but not too much. A mixing machine is like a giant food processor, and like the food processor, its dynamics is deterministic but chaotic. The mathematics of chaos has provided a new understanding of mixing processes and led to some improved designs. The methods used to detect chaos in data have inspired new test equipment for the wire used to make springs, improving efficiency in spring- and wire-making. The humble spring has many vital uses: it can be found in mattresses, cars, DVD players, even ballpoint pens. Chaotic control, a technique that uses the butterfly effect to keep dynamic behaviour stable, is showing promise in the design of more efficient and less intrusive heart pacemakers.

Overall, though, the main impact of chaos has been on scientific thinking. In the forty years or so since its existence started to be widely appreciated, chaos has changed from a minor mathematical curiosity into a basic feature of science. We can now study many of nature's irregularities without resorting to statistics, by teasing out the hidden patterns that characterise deterministic chaos. This is just one of the ways in which modern dynamical systems theory, with its emphasis on nonlinear behaviour, is causing a quiet revolution in the way scientists think about the world.

 

 

 

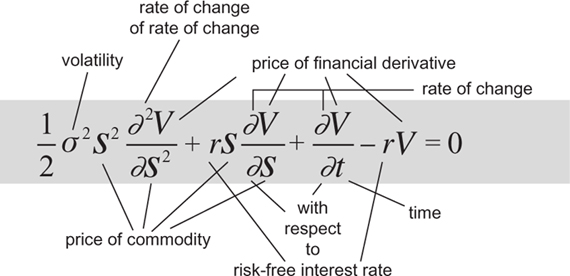
It describes how the price of a financial derivative changes over time, based on the principle that when the price is correct, the derivative carries no risk and no one can make a profit by selling it at a different price.

It makes it possible to trade a derivative before it matures by assigning an agreed ‘rational' value to it, so that it can become a virtual commodity in its own right.

Massive growth of the financial sector, ever more complex financial instruments, surges in economic prosperity punctuated by crashes, the turbulent stock markets of the 1990s, the 2008–9 financial crisis, and the ongoing economic slump.

S
ince the turn of the century the greatest source of growth in the financial sector has been in financial instruments known as derivatives. Derivatives are not money, nor are they investments in stocks and shares. They are investments in investments, promises about promises. Derivatives traders use virtual money, numbers in a computer. They borrow it from investors who have probably borrowed it from somewhere else. Often they haven't borrowed it at all, not even virtually: they have clicked a mouse to agree that they
will
borrow the money if it ever becomes necessary. But they have no intention of letting it become necessary; they will sell the derivative before that happens. The lender – hypothetical lender, since the loan will never occur, for the same reason – probably doesn't actually have the money either. This is finance in cloud cuckoo land, yet it has become the standard practice of the world's banking system.

Unfortunately, the consequences of derivatives trading do, ultimately, turn into real money, and real people suffer. The trick works, most of the time, because the disconnect with reality has no notable effect, other than making a few bankers and traders extremely rich as they siphon off real money from the virtual pool. Until things go wrong. Then the pigeons come home to roost, bearing with them virtual debts that have to be paid with real money. By everyone else, naturally.

This is what triggered the banking crisis of 2008-9, from which the world's economies are still reeling. Low interest rates and enormous personal bonus payments encouraged bankers and their banks to bet ever larger sums of virtual money on ever more complex derivatives, ultimately secured – so they believed – in the property market, houses and businesses. As the supply of suitable property and people to buy it began to dry up, the financial world's leaders needed to find new ways to convince shareholders that they were creating profit, in order to justify and finance their bonuses. So they started trading packages of debt, also allegedly secured, somewhere down the line, on real property. Keeping the scheme going demanded the continued purchase of property, to increase the pool of collateral. So the banks started selling mortgages to people whose ability to repay them was
increasingly doubtful. This was the subprime mortgage market, ‘subprime' being a euphemism for ‘likely to default'. Which soon became ‘certain to default'.