In Pursuit of the Unknown (58 page)

The data suggest unequivocally that extreme events are nowhere near as rare as Brownian motion predicts. The probability distribution does not die way exponentially (or faster); it dies away like a power-law curve
x
^–a
for some positive constant
a
. In the financial jargon, such a distribution is said to have a
fat tail
. Fat tails indicate increased levels of risk. If your investment has a five-sigma expected return, then assuming Brownian motion, the chance that it will fail is less than one in a million. But if tails are fat, it might be much larger, maybe one in a hundred. That makes it a much poorer bet.

A related term, made popular by Nassim Nicholas Taleb, an expert in mathematical finance, is ‘black swan event'. His 2007 book
The Black Swan
became a major bestseller. In ancient times, all known swans were white. The poet Juvenal refers to something as ‘a rare bird in the lands, and very like a black swan', and he meant that it was impossible. The phrase was widely used in the sixteenth century, much as we might refer to a flying pig. But in 1697, when the Dutch explorer Willem de Vlamingh went to the aptly named Swan River in Western Australia, he found masses of black swans. The phrase changed its meaning, and now refers to an assumption
that appears to be grounded in fact, but might at any moment turn out to be wildly mistaken. Yet another term current is X-event, ‘extreme event'.

These early analyses of markets in mathematical terms encouraged the seductive idea that the market could be modelled mathematically, creating a rational and safe way to make unlimited sums of money. In 1973 it seemed that the dream might become real, when Fischer Black and Myron Scholes introduced a method for pricing options: the Black–Scholes equation. Robert Merton provided a mathematical analysis of their model in the same year, and extended it. The equation is:

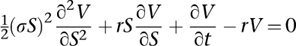
It involves five distinct quantities – time
t
, the price
S
of the commodity, the price
V
of the derivative, which depends on
S
and
t
, the risk-free interest rate
r
(the theoretical interest that can be earned by an investment with zero risk, such as government bonds), and the volatility
σ
²
of the stock. It is also mathematically sophisticated: a second-order partial differential equation like the wave and heat equations. It expresses the rate of change of the price of the derivative, with respect to time, as a linear combination of three terms: the price of the derivative itself, how fast that changes relative to the stock price, and how that change accelerates. The other variables appear in the coefficients of those terms. If the terms representing the price of the derivative and its rate of change were omitted, the equation would be exactly the heat equation, describing how the price of the option diffuses through stock-price-space. This traces back to Bachelier's assumption of Brownian motion. The other terms take additional factors into account.

The Black–Scholes equation was derived as a consequence of a number of simplifying financial assumptions – for instance, that there are no transaction costs and no limits on short-selling, and that it is possible to lend and borrow money at a known, fixed, risk-free interest rate. The approach is called arbitrage pricing theory, and its mathematical core goes back to Bachelier. It assumes that market prices behave statistically like Brownian motion, in which both the rate of drift and the market volatility are constant. Drift is the movement of the mean, and volatility is financial jargon for standard deviation, a measure of average divergence from the mean. This assumption is so common in the financial literature that it has become an industry standard.

There are two main kinds of option. In a put option, the buyer of the option purchases the right to sell a commodity or financial instrument at a specified time for an agreed price, if they so wish. A call option is similar, but it confers the right to buy instead of sell. The Black–Scholes equation has explicit solutions: one formula for put options, another for call options.
¹
If such formulas had not existed, the equation could still have been solved numerically and implemented as software. However, the formulas make it straightforward to calculate the recommended price, as well as yielding important theoretical insights.

The Black–Scholes equation was devised to bring a degree of rationality to the futures market, which it does very effectively under normal market conditions. It provides a systematic way to calculate the value of an option
before it matures
. Then it can be sold. Suppose, for instance, that a merchant contracts to buy 1000 tons of rice in 12 months' time at a price of 500 per ton – a call option. After five months she decides to sell the option to anyone willing to buy it. Everyone knows how the market price for rice has been changing, so how much is that contract worth right now? If you start trading such options without knowing the answer, you're in trouble. If the trade loses money, you're open to the accusation that you got the price wrong and your job could be at risk. So what should the price be? Trading by the seat of your pants ceases to be an option when the sums involved are in the billions. There has to be an agreed way to price an option at any time before maturity. The equation does just that. It provides a formula, which anyone can use, and if your boss uses the same formula, he will get the same result that you did, provided you didn't make errors of arithmetic. In practice, both of you would use a standard computer package.

The equation was so effective that it won Merton and Scholes the 1997 Nobel Prize in Economics.
²
Black had died by then, and the rules of the prize prohibit posthumous awards, but his contribution was explicitly cited by the Swedish Academy. The effectiveness of the equation depended on the market behaving itself. If the assumptions behind the model ceased to hold, it was no longer wise to use it. But as time passed and confidence grew, many bankers and traders forgot that; they used the equation as a kind of talisman, a bit of mathematical magic that protected them against criticism. Black–Scholes not only provides a price that is reasonable under normal conditions; it also covers your back if the trade goes belly-up. Don't blame me, boss, I used the industry standard formula.

The financial sector was quick to see the advantages of the Black–Scholes equation and its solutions, and equally quick to develop a host of related equations with different assumptions aimed at different financial instruments. The then-sedate world of conventional banking could use the equations to justify loans and trades, always keeping an eye open for potential trouble. But less conventional businesses would soon follow, and they had the faith of a true convert. To them, the possibility of the model going wrong was inconceivable. It became known as the Midas formula – a recipe for making everything turn to gold. But the financial sector forgot how the story of King Midas ended.

The darling of the financial sector, for several years, was a company called Long Term Capital Management (LTCM). It was a hedge fund, a private fund that spreads its investments in a way that is intended to protect investors when the market goes down, and make big profits when it goes up. It specialised in trading strategies based on mathematical models, including the Black–Scholes equation and its extensions, together with techniques such as arbitrage, which exploits discrepancies between the prices of bonds and the value that can actually be realised. Initially LTCM was a spectacular success, yielding returns in the region of 40% per year until 1998. At that point it lost $4.6 billion in under four months, and the Federal Reserve Bank persuaded its major creditors to bail it out to the tune of $3.6 billion. Eventually the banks involved got their money back, but LTCM was wound up in 2000.

What went wrong? There are as many theories as there are financial commentators, but the consensus is that the proximate cause of LTCM's failure was the Russian financial crisis of 1998. Western markets had invested heavily in Russia, whose economy was heavily dependent on oil exports. The Asian financial crisis of 1997 caused the price of oil to slump, and the main casualty was the Russian economy. The World Bank provided a loan of $22.6 billion to prop the Russians up.

The ultimate cause of LTCM's demise was already in place on the day it started trading. As soon as reality ceased to obey the assumptions of the model, LTCM was in deep trouble. The Russian financial crisis threw a spanner in the works that demolished almost all of those assumptions. Some factors had a bigger effect than others. Increased volatility was one of them. Another was the assumption that extreme fluctuations hardly ever occur: no fat tails. But the crisis sent the markets into turmoil, and in the panic, prices dropped by huge amounts – many sigmas – in seconds. Because all of the factors concerned were interrelated, these events triggered other rapid changes, so rapid that traders could not possibly
know the state of the market at any instant. Even if they wanted to behave rationally, which people don't do in a general panic, they had no basis upon which to do so.

If the Brownian model is right, events as extreme as the Russian financial crisis should occur no more often than once a century. I can remember seven from personal experience in the past 40 years: overinvestment in property, the former Soviet Union, Brazil, property (again), property (yet again), dotcom companies, and. . . oh, yes, property.

With hindsight, the collapse of LTCM was a warning. The dangers of trading by formula in a world that did not obey the cosy assumptions behind the formula were duly noted – and quickly ignored. Hindsight is all very well, but anyone can see the danger after a crisis has struck. What about foresight? The orthodox claim about the recent global financial crisis is that, like the first swan with black feathers, no one saw it coming.

That's not entirely true.

The International Congress of Mathematicians is the largest mathematical conference in the world, taking place every four years. In August 2002 it took place in Beijing, and Mary Poovey, professor of humanities and director of the Institute for the Production of Knowledge at New York University, gave a lecture with the title ‘Can numbers ensure honesty?'
³
The subtitle was ‘unrealistic expectations and the US accounting scandal', and it described the recent emergence of a ‘new axis of power' in world affairs:

This axis runs through large multinational corporations, many of which avoid national taxes by incorporating in tax havens like Hong Kong. It runs through investment banks, through nongovernmental organizations like the International Monetary Fund, through state and corporate pension funds, and through the wallets of ordinary investors. This axis of financial power contributes to economic catastrophes like the 1998 meltdown in Japan and Argentina's default in 2001, and it leaves its traces in the daily gyrations of stock indexes like the Dow Jones Industrials and London's Financial Times Stock Exchange 100 Index (the FTSE).

She went on to say that this new axis of power is intrinsically neither good nor bad: what matters is how it wields its power. It helped to raise China's standard of living, which many of us would consider to be beneficial. It
also encouraged a worldwide abandonment of welfare societies, replacing them by a shareholder culture, which many of us would consider to be harmful. A less controversial example of a bad outcome is the Enron scandal, which broke in 2001. Enron was an energy company based in Texas, and its collapse led to what was then the biggest bankruptcy in American history, and a loss to shareholders of $11 billion. Enron was another warning, this time about deregulated accounting laws. Again, few heeded the warning.

Poovey did. She pointed to the contrast between the traditional financial system based on the production of real goods, and the emerging new one based on investment, currency trading, and ‘complex wagers that future prices would rise or fall'. By 1995 this economy of virtual money had overtaken the real economy of manufacturing. The new axis of power was deliberately confusing real and virtual money: arbitrary figures in company accounts and actual cash or commodities. This trend, she argued, was leading to a culture in which the values of both goods and financial instruments were becoming wildly unstable, liable to explode or collapse at the click of a mouse.

The article illustrated these points using five common financial techniques and instruments, such as ‘mark to market accounting', in which a company sets up a partnership with a subsidiary. The subsidiary buys a stake in the parent company's future profits; the money involved is then recorded as instant earnings by the parent company while the risk is relegated to the subsidiary's balance sheet. Enron used this technique when it changed its marketing strategy from selling energy to selling energy futures. The big problem with bringing forward potential future profits in this manner is that they cannot then be listed as profits next year. The answer is to repeat the manoeuvre. It's like trying to drive a car without brakes by pressing ever harder on the accelerator. The inevitable result is a crash.