In Pursuit of the Unknown (47 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Leaving aside the perplexing realm of cosmology, there are now more homely ways to verify relativity, both special and general, on a human scale. Special relativity can be tested in the laboratory, and modern measuring techniques provide exquisite accuracy. Particle accelerators such as the Large Hadron Collider simply would not work unless the designers took special relativity into account, because the particles that whirl round these machines do so at speeds very close indeed to that of light. Most tests of general relativity are still astronomical, ranging from gravitational lensing to pulsar dynamics, and the level of accuracy is high. A recent NASA experiment in low-Earth orbit, using high-precision gyroscopes, confirmed the occurrence of inertial frame-dragging, but failed to reach the intended precision because of unexpected electrostatic effects. By the time the data were corrected for this problem, other experiments had already achieved the same results.
However, one instance of relativistic dynamics, both special and general, is closer to home: car satellite navigation. The satnav systems used by motorists calculate the car's position using signals from a network of 24 orbiting satellites, the Global Positioning System. GPS is astonishingly accurate, and it works because modern electronics can reliably handle and measure very tiny instants of time. It is based on very precise timing signals, pulses emitted by the satellites and picked up on the ground. Comparing the signals from several satellites triangulates the location of the receiver to within a few metres. This level of accuracy requires knowing the timing to within about 25 nanoseconds (billionths of a second). Newtonian dynamics doesn't give correct locations, because two effects that are not accounted for in Newton's equations alter the flow of time: the satellite's motion and Earth's gravitational field.
Special relativity deals with the motion, and it predicts that the atomic clocks on the satellites should lose 7 microseconds (millionths of a second)
per day compared with clocks on the ground, thanks to relativistic time dilation. General relativity predicts a gain of 45 microseconds per day caused by the Earth's gravity. The net result is that the clocks on the satellites gain 38 microseconds per day for relativistic reasons. Small as this may seem, its effect on GPS signals is by no means negligible. An error of 38 microseconds is 38,000 nanoseconds, about 1500 times the error that GPS can tolerate. If the software calculated your car's location using Newtonian dynamics, your satnav would quickly become useless, because the error would grow at a rate of 10 kilometres per day. Ten minutes from now Newtonian GPS would place you on the wrong street; by tomorrow it would place you in the wrong town. Within a week you'd be in the wrong county; within a month, the wrong country. Within a year, you'd be on the wrong planet. If you disbelieve relativity, but use satnav to plan your journeys, you have some explaining to do.
| 14 | Quantum weirdness |
Â
Â
Â
Â
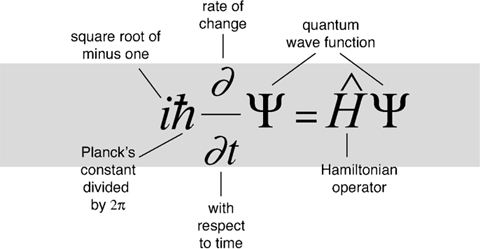
The equation models matter not as a particle, but as a wave, and describes how such a wave propagates.
Schrödinger's equation is fundamental to quantum mechanics, which together with general relativity constitute today's most effective theories of the physical universe.
A radical revision of the physics of the world at very small scales, in which every object has a âwave function' that describes a probability cloud of possible states. At this level the world is inherently uncertain. Attempts to relate the microscopic quantum world to our macroscopic classical world led to philosophical issues that still reverberate. But experimentally, quantum theory works beautifully, and today's computer chips and lasers wouldn't work without it.
I
n 1900 the great physicist Lord Kelvin declared that the then current theory of heat and light, considered to be an almost complete description of nature, was âobscured by two clouds. The first involves the question: How could the Earth move through an elastic solid, such as is essentially the luminiferous ether? The second is the Maxwell-Boltzmann doctrine regarding the partition of energy.' Kelvin's nose for an important problem was spot on. In
Chapter 13
we saw how the first question led to, and was resolved by, relativity. Now we will see how the second led to the other great pillar of present-day physics, quantum theory.
The quantum world is notoriously weird. Many physicists feel that if you don't appreciate just how weird it is, you don't appreciate it at all. There is a lot to be said for that opinion, because the quantum world is so different from our comfortable human-scale one that even the simplest concepts change out of all recognition. It is, for example, a world in which light is both a particle and a wave. It is a world where a cat in a box can be both alive and dead at the same time. . . until you open the box, that is, when suddenly the unfortunate animal's wave function âcollapses' to one state or the other. In the quantum multiverse, there exists one copy of our universe in which Hitler lost World War II, and another in which he won it. We just happen to live in â that is, exist as quantum wave functions in â the first one. Other versions of us, just as real but inaccessible to our senses, live in the other one.
Quantum mechanics is definitely weird. Whether it is quite
that
weird, though, is another matter altogether.
It all began with light bulbs. This was appropriate, because those were one of the most spectacular applications to emerge from the burgeoning subjects of electricity and magnetism, which Maxwell so brilliantly unified. In 1894 a German physicist named Max Planck was hired by an electrical company to design the most efficient light bulb possible, one giving the most light while consuming the least electrical energy. He saw that the key to this question was a fundamental issue in physics, raised in 1859 by
another German physicist, Gustav Kirchhoff. It concerned a theoretical construct known as a black body, which absorbs all electromagnetic radiation that falls on it. The big question was: how does such a body
emit
radiation? It can't store it all; some has to come back out again. In particular, how does the intensity of the emitted radiation depend on its frequency and the body's temperature?
There was already an answer from thermodynamics, in which a black body can be modelled as a box whose walls are perfect mirrors. Electromagnetic radiation bounces to and fro, reflected by the mirrors. How is the energy in the box distributed among the various frequencies when the system has settled to an equilibrium state? In 1876 Boltzmann proved the âequipartition theorem': the energy is apportioned equally to each independent component of the motion. These components are just like the basic waves in a violin string: normal modes.
There was only one problem with this answer: it couldn't possibly be correct. It implied that the total power radiated over all frequencies must be infinite. This paradoxical conclusion became known as the ultraviolet catastrophe: ultraviolet because that was the beginning of the high-frequency range, and catastrophe because it was. No real body can emit an infinite amount of power.
Although Planck was aware of this problem, it didn't bother him, because he didn't believe the equipartition theorem anyway. Ironically, his work resolved the paradox and did away with the ultraviolet catastrophe, but he noticed this only later. He used experimental observations of how energy depended on frequency, and fitted a mathematical formula to the data. His formula, derived early in 1900, did not initially have any physical basis. It was just a formula that worked. But later the same year he tried to reconcile his formula with the classical thermodynamic one, and decided that the energy levels of the black body's vibrational modes could not form a continuum, as thermodynamics assumed. Instead, these levels had to be discrete â separated by tiny gaps. In fact, for any given frequency, the energy had to be an integer multiple of that frequency, multiplied by a very tiny constant. We now call this number Planck's constant and denote it by
h
. Its value, in units of joule seconds, is 6.62606957(29) Ã 10
â34
, where the figures in brackets may be inaccurate. This value is deduced from theoretical relationships between Planck's constant and other quantities that are easier to measure. The first such measurement was made by Robert Millikan using the photoelectric effect, described below. The tiny packets of energy are now called quanta (plural of quantum), from the Latin
quantus
, âhow much.'
Planck's constant may be tiny, but if the set of energy levels for a given frequency is discrete, the total energy turns out to be finite. So the ultraviolet catastrophe was a sign that a continuum model failed to reflect nature. And that implied that nature, on very small scales, must be discrete. Initially this didn't occur to Planck: he thought of his discrete energy levels as a mathematical trick to get a sensible formula. In fact, Boltzmann had entertained a similar idea in 1877, but didn't get anywhere with it. Everything changed when Einstein brought his fertile imagination to bear, and physics entered a new realm. In 1905, the same year as his work on special relativity, he investigated the photoelectric effect, in which light hitting a suitable metal causes it to emit electrons. Three years earlier Philipp Lenard had noticed that when the light has a higher frequency, the electrons have higher energies. But the wave theory of light, amply confirmed by Maxwell, implies that the energy of the electrons should depend on the intensity of the light, not on its frequency. Einstein realised that Planck's quanta would explain the discrepancy. He suggested that light, rather than being a wave, was composed of tiny particles, now called photons. The energy in a single photon, of a given frequency, should be the frequency times Planck's constant â just like one of Planck's quanta. A photon was a quantum of light.
There's an obvious problem with Einstein's theory of the photoelectric effect: it assumes light is a particle. But there was abundant evidence that light was a wave. On the other hand, the photoelectric effect was incompatible with light being a wave. So was light a wave, or a particle?
Yes.
It was â or had aspects that manifested themselves as â either. In some experiments, light seemed to behave like a wave. In others, it behaved like a particle. As physicists came to grips with very small scales of the universe, they decided that light wasn't the only thing to have this strange dual nature, sometimes particle, sometimes wave. All matter did. They called it wave-particle duality. The first person to grasp this dual nature of matter was Louis-Victor de Broglie, in 1924. He rephrased Planck's law in terms not of energy, but of momentum, and suggested that the momentum of the particle aspect and the frequency of the wave aspect should be related: multiply them together and you get Planck's constant. Three years later he was proved right, at least for electrons. One the one hand, electrons are particles, and can be observed behaving that way. On the other hand, they
diffract like waves. In 1988 atoms of sodium were also spotted behaving like a wave.
Matter was neither particle nor wave, but a bit of both â a wavicle.
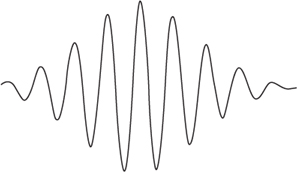
Several more or less intuitive images of this dual nature of matter were devised. In one, a particle is a localised clump of waves, known as a wave packet,
Figure 54
. The packet as a whole can behave like a particle, but some experiments can probe its internal wavelike structure. Attention shifted from providing images for wavicles to sorting out how they behaved. The quest quickly attained its goal, and the central equation of quantum theory emerged.