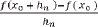Mathematics and the Real World (53 page)

Does that sound complicated? Indeed, the definition is a complicated one. We have already made the point that if a formulation has many quantifiers, and here we have at least three and the order in which they appear is also important, we cannot grasp it intuitively. If there are among our readers some who completed a course in differential calculus, they may have encountered this definition at that stage, but they will surely also
remember the difficulties, or even nightmares, that this and similar definitions caused them and their colleagues.

When the concept of a limit is clear, the concept of the derivative of a function
f
(
x
) at point
x
₀
can be defined as follows:

The derivative is the limit of the numbers

for every sequence of numbers
h
_n
that are different from 0 whose limit is 0.

Does that sound complicated? Indeed. Yet note, the definition is based on only numbers and is independent of geometry. The motivation for the definition, namely, the slope of the tangent, is geometric, but the definition itself does not use geometry.

The point should be made, and it will be repeated in connection with other developments, that the purpose of this rigorous development was not to give a better understanding of the concepts. We will go further and say that for a better understanding of the concepts they should be illustrated by a geometric drawing. The incentive behind the development was similar to that driving the Greeks, an attempt to prevent errors deriving from geometric illusions.

Basing infinitesimal calculus on numbers avoided the need to rely directly on geometric axioms, but it did not avoid indirect dependence on geometry, because the definition of the numbers was itself geometric. An example we have quoted previously is the definition of irrational numbers such as √2, defined as the length of the diagonal of a square with sides of length 1. With this realization, attempts began to provide a non-geometric base for irrational numbers themselves. Two of Germany's leading mathematicians at that time, Karl Weierstrass, mentioned in the previous section, and Bernhard Bolzano (1781–1848) based the concept of an irrational number on the limits of numbers. Thus, √2 would be defined as the limit of positive rational numbers, say
r
_n
, that satisfy the requirement that the series (
r
_n
)
²
itself has a limit, and that is the whole number 2. Later, the German mathematician Richard Dedekind (1831–1916) proposed a different
definition of irrational numbers. His definition uses what is named after him, that is, Dedekind cuts, and is the definition that is taught still today in mathematics classes in universities.

The number
√
2, for example, is defined as the pair of sets of rational numbers, say (
R
₁
,
R
₂
), where
R
₁
is the set of rational numbers in which each one is smaller than a rational number the square of which is smaller than 2, and
R
₂
is the set of rational numbers in which each one is larger than a rational positive number the square of which is greater than 2. Other irrational numbers are similarly defined as pairs of sets of rational numbers.

To the reader who has not personally experienced this type of definition in the past, this will seem strange. A single number, whose meaning is clear and has been clear for thousands of years, is now defined as a pair of sets of rational numbers. Yet this is the price to be paid for the aspiration to avoid geometry. The definition of irrational numbers by means of Dedekind cuts was not intended to make it any easier to understand what an irrational number is. No one thinks he is clarifying what an irrational number is by presenting it as a pair of sets of numbers. The geometric definition is in fact simpler and more comprehensible. The reason for this development was to avoid using geometric language, even if by so doing it greatly complicated the concepts.

Defining irrational numbers without resorting to geometry did not entirely remove geometry from the picture, as rational numbers, sets of which are used to define irrational numbers, are also defined geometrically, based on the plane axioms. Again, the need arose to define the rational numbers without geometry. I will now present a development that I learned in my first class in university. It will be relevant to the last part of this book, but the details can be omitted without losing the main message.

Let us agree that we know what the natural numbers are, that is, 1, 2, 3, and so on, and we also know how to add and multiply the natural numbers. We now define the positive rational numbers.

First, we look at pairs of natural numbers (
a
,
b
) (the explanation, which helps us understand but which may not be used in the definition, is that (
a
,
b
) is the rational number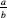
). We define equivalent pairs thus: the pair (
a
,
b
) is equivalent to the pair (
c
,
d
) if
ad
=
bc
(according to our explanation, the equivalence does ensure the equality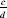
=
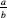, in other words, that it is the same rational number). Once we have understood what equivalence means, we can define a positive rational number as follows: a positive rational number is a collection of pairs, with the numbers in each pair equivalent to each other. In addition, addition and multiplication of the rational numbers must also be defined. We define the addition of (
a
,
b
) and (
c
,
d
) as the collection of pairs equivalent to (
ad
+
cb
,
bd
), and their product as the collection of pairs equivalent to (
ac
,
bd
) (we suggest that the reader check the operations in light of the interpretation).

These definitions reflect what we understand by the term
rational numbers
, and they are entirely free of dependence on geometry. It should be repeated and stressed that it is difficult to understand the definitions without relating to the intuitive grasp of rational numbers, and the only reason for this somewhat strange presentation of the definitions of quantities that we all essentially understand, is the desire to avoid reliance on geometry. Thus, as we have seen, irrational numbers, and hence the real number line, can be defined without resort to geometry.

Note that these definitions, and others that we have not included here, use the natural numbers and also the concept of a set. The sets were used in the definition of rational numbers, via equivalence of sets, and also in the definition of irrational numbers, via Dedekind cuts.

59. NUMBERS AS SETS, LOGIC AS SETS

The reliance on sets in the development of the foundations of mathematics, and in particular the redefinition of numbers on the straight line, the definition of limits and hence calculus, was in general accepted and greatly welcomed by the mathematics community. With regard to applications, it can be shown that all results previously proved geometrically were correct also on the basis of set theory. For example, the equality √2√3 = √6 can be proven by geometry but can be proven more simply using Dedekind cuts (to do this we must define and understand the product of two cuts; we will spare the reader that step). It was even more satisfying to view this from the aspect of the foundations of mathematics. Indeed, as George Boole showed, there is full parallelism between sets and the natural operations that can be performed on them on the one hand, and logical arguments
on the other (Boole developed this believing that was the way to analyze probabilistic events, as mentioned above in section 41). Some examples follow.

The parallelism between sets and logical propositions can be seen when we consider a claim to mean the set of all the possibilities of satisfying it. For example, we will take the claim “it is raining” to mean the set of all the situations in which it is raining, and the claim that “the sky is blue” will refer to all the situations in which the sky is blue.

We will examine the relation between two claims, say P and Q, and compare it to the relation between two sets, say A and B. The statement “either P holds (i.e., is true) or Q holds” is equivalent to taking the union of the two sets, that is, all the elements contained in A or B. Likewise, “it is raining or the sky is blue” is equivalent to the union of the sets of situations in which it is raining and those when the sky is blue. The proposition “both P and Q hold” is equivalent to the intersection of the two sets, that is, the elements contained both in A and in B. The intersection is denoted A∩B. The claim “P does not hold” is equivalent to taking the complement of the set A, in other words, all the elements not in A. In this way, every logical argument can be stated in terms of sets. Thus, the statement “P and Q cannot both hold” can be translated into the statement that A∩B is an empty set. Such sets are also known as disjoint sets. The proposition “it is not possible that is raining and the sky is blue” can be translated into the language of sets thus: “the intersection of the ‘rain’ set of situations and the ‘blue sky’ set of situations is an empty set,” that is, they are disjoint sets. Numbers can also be based on sets, by counting the elements in the sets (this will be described shortly).