Mathematics and the Real World (57 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Another axiom also played a major role in the attempts to answer the question, and that is the axiom of choice, a highly intuitive claim when referring to a world about which human beings developed intuition. It says that given a collection of non-empty sets, a new set can be formed by selecting one member from each set in the collection. Such a selection is simple if the collection of sets is finite, but we have already seen that the concept of infinity can be deceptive. The axiom of choice was indeed recognized as an axiom, and the question of what would happen if it was added to the Zermelo-Fraenkel axioms remained unanswered.
Gödel himself contributed to the answer to this question and proved that if the Zermelo-Fraenkel system is consistent, that is, it does not contain contradictions (which has not been proven), adding the axiom of choice to the system will leave it consistent. Then Gödel added a slightly confusing finding: if the Zermelo-Fraenkel system is consistent, even if we add the axiom of choice to it, it will be impossible to prove that C =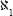 . Prior to the incompleteness theorem, this result would have ended the search for the truth: if it is impossible to prove the correctness of a particular claim, and if everything can be proven or disproven, then the claim is incorrect. In the world after the incompleteness theorem, however, there is another possibility, that the theorem is one of those the truth of which is impossible to resolve.
. Prior to the incompleteness theorem, this result would have ended the search for the truth: if it is impossible to prove the correctness of a particular claim, and if everything can be proven or disproven, then the claim is incorrect. In the world after the incompleteness theorem, however, there is another possibility, that the theorem is one of those the truth of which is impossible to resolve.
In 1964 Paul Cohen (1934–2007), a young mathematician from
Stanford University, showed that the continuum hypothesis was in that category. Moreover, he showed that if the Zermelo-Fraenkel system is consistent, the claim C =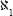 or its negation can be added to the system without affecting its consistency. The question of whether the Zermelo-Fraenkel system is consistent, meaning, does not contain contradictions, is still unanswered today.
or its negation can be added to the system without affecting its consistency. The question of whether the Zermelo-Fraenkel system is consistent, meaning, does not contain contradictions, is still unanswered today.
Research along these avenues, that is, the attempts to find a system of logic without contradictions on which mathematics can be based without doubts or uncertainties, continues. On the one hand, research into Gödel's theorem shows that the phenomenon is very general. For instance, Gödel's proof of the incompleteness theorem was based on the liar's paradox, that is, on a claim that relates to itself. Since then proofs have been found that do not use claims that relate to themselves so that we cannot dispose of incompleteness merely by not allowing claims that relate to themselves. On the other hand, the various attempts to find ever-more complete systems sometimes yielded strange results. For example, as the axiom of choice seems intuitive, we can define other axioms, no less intuitive, that contradict the axiom of choice but whose status regarding the basic axioms of set theory is the same as that of the axiom of choice. That is to say, even if we add them to the Zermelo-Fraenkel system we will not find a contradiction (provided, of course, that the Zermelo-Fraenkel system is consistent).
So what is the correct mathematics? Does mathematics that is correct beyond all doubt exist? The answer is clear: we do not know. At this stage there is room for faith. Some believe that in the world, the physical world and the Platonic ideal world, there is a correct mathematics, but we just have not found it yet. In that mathematics, for example, Goldbach's conjecture is definitely correct or incorrect. Similarly, in that mathematics, either the equality C =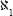 is fulfilled or it is not. Others believe that there is no such absolute truth. Mathematics rests on the axioms that define it, and different systems of axioms yield different types of mathematics, possibly even contradictory ones, and we must learn to live with that dichotomy. But most mathematicians simply do not care. The many years of involvement in mathematics have resulted in faith that there is no basic contradiction
is fulfilled or it is not. Others believe that there is no such absolute truth. Mathematics rests on the axioms that define it, and different systems of axioms yield different types of mathematics, possibly even contradictory ones, and we must learn to live with that dichotomy. But most mathematicians simply do not care. The many years of involvement in mathematics have resulted in faith that there is no basic contradiction
in mathematics, and we can continue to work. If the logicians manage to arrive at absolute mathematical truth, whether via axioms or some other way, all the better. But even if not, even without any logical “proof beyond doubt,” the mathematics we produce is correct beyond any doubt.
What does a mathematician do when he gets to the office in the morning? • How does sleep help to solve problems in mathematics? • Does creativity in mathematics decline with age? • Why would a mathematician refuse to accept a million dollars? • Does pure mathematics exist? • Why did the engines of steamships start exploding? • Can aliens do the sum 2 + 2?
62. HOW DOES A MATHEMATICIAN THINK?
We will start with the bottom line: there is no difference between the thought process of a mathematician and those in other disciplines. Before we clarify this issue, we must explain what we mean when we use the word
think
. Thinking means activating the brain to analyze situations, reach conclusions, and propose courses of action or solutions. With regard to these functions, there are various levels of brain activity, and we will concentrate on two that are related but different. The first type of thinking takes place in situations in which you have to carry out an action about which you have received previous guidance on how to proceed. For example, you have been given a cake recipe, and now you have to make that cake. Or, someone explained to you how to use a road map, and now you have to find the route from one place to another. Or, you have been taught how to use a paintbrush and oil paints to paint a still life, and now you wish to paint flowers in a vase. Or, you have learned how to design a car engine, and now you have to design one. Or, you have been taught how to solve a
certain type of exercise in algebra, and in an examination you have to solve an exercise of that sort. All of the above need thought, and the thought process is matching the required process to those learned or tried in one way or another. We will call such thinking
thinking by comparison
.
The second type of thinking occurs when we use our brain to react to an unfamiliar situation in which we have not learned how to operate, or in which we consciously want to deviate from the normal course of action. For example, you are on a desert island, you have to put together a meal from the vegetation you can find, and you do not even know if the various plants are edible. Or, you have reached an unfamiliar location and have to find your way without a road map. Or, you have artists’ materials in front of you, and you have decided to paint a picture in a completely new, unfamiliar style. Or, you have to design a vehicle that will be able to move on an asteroid, the nature of whose surface is unknown. Or, you are trying to find a mathematical characteristic of an unknown system that no one has researched. In such situations, creative thinking is needed.
The two types of thinking are not detached from each other. Even when comparative thinking is called for, in general there are differences between the situation previously encountered and the current one, and a measure of creativity will be necessary to match the solution properly to the new situation. Where new situations are encountered and creative thinking is required, creativity is not ex nihilo, and elements of comparative thinking will play a part. Comparative thinking focuses on searching and matching, which are essentially routine, sometimes automatic, operations and can even be performed by a computer. The other type of thinking, in contrast, is based mainly on intuition, feeling, hunches. When a person has to deal with a problem, the brain will “decide” whether to activate comparative thinking or to enlist creative intuition according to the person's familiarity with that or similar problems. The brain's “decision” is not generally a conscious one.
Thinking by comparison cannot be taught or learned in isolation from the subject; in other words, this method of thinking cannot be learned in the abstract. In every subject, from cooking, through engineering, to mathematics, more and more can be learned to a level such that additional problems will be within a person's knowledge so that he can make do with
comparative thinking and shorten the route to an appropriate solution. Unlike comparative thinking, creative thinking cannot be taught or learned at all. Creative, intuitive thinking can only be encouraged and stimulated. Trying to teach creative thinking via examples is a positive step, but the effect of the examples is simply to enrich the collection of problems that can be solved by comparative thinking. With regard to intuition itself, the more you know, the more you will be able to widen the sphere in which you can exercise creativity, but we do not know enough about how human intuition works to be able to teach people how to develop their creative intuition.
Once we have understood what thinking is, we can repeat: there is no difference between the thinking of mathematicians and the thinking of those in other professions. Obviously they think about different subjects. Cooking, finding your way somewhere, painting, engineering, and mathematics are highly dissimilar, but the types of thinking and the methods of thinking are the same in all of them. The myth that to be a mathematician you need a special type of brain is just as correct, or incorrect, as saying that to be a chef you need a special type of brain, and the same applies to the ability to navigate or to introduce novel ways of painting. Research in mathematics for the most part deals with new developments and is more closely related to the creative type of thinking, but the same could be said of creative research in any subject. One difference between research in mathematics and other research is that the intuition required in mathematical activity needs more thinking time. That is because research in mathematics deals mainly with logical aspects, and these are less at home among the brain's abilities as formed by evolution. The expression “Wait a moment, give me time to think about it” comes up more often in mathematical discussions than in conversations about cooking or navigating a route. Therefore, for most of their research time, mathematicians are immersed in reflection and intuitive thinking. Only after they have reached a solution intuitively do they start work on recording the solution in the acceptable language of logic. Henri Poincaré is credited with having said, “It is by logic that we prove, but by intuition that we discover.” The proof stage itself, however, belongs essentially in the first, more technical, type of thinking.

