Mathematics and the Real World (61 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Of course the collection of integers is a group where the operation is addition. The natural numbers are not a group because it does not have the inverse property. The positive real numbers are also a group when the operation is multiplication, and the zero member is the number 1. There are also groups with a finite number of members, for instance when the members of the group are revolutions of the plane by multiples of 90 degrees, as described in section 31. Abstract group theory tries to reveal mathematical properties of groups relying solely on the simple definition of a group. As soon as such a property is proven, it applies to all examples of groups.
In addition to groups, mathematicians also define collections with other properties, for example, fields.
A field is a group on which, in addition to the operation of addition, another operation can be performed, and we will denote the additional operation by a point · like the multiplication point, and we will also call it “multiplication.” The multiplication operation also has the associativity property, and it also has a neutral member that we will denote by the symbol 1 (again, not the number 1), and every element
a
that is not equal to 0 has an inverse that we will denote by
a
–1
. There is a connection between the addition and multiplication operations, and it is known as distributivity, that is, for all three elements in the field, the equation
a
· (
b
+
c
) =
a
·
b
+
a
·
c
holds. Here again the symbols are familiar to us from their use with numbers, and indeed the numbers are a field, but the purpose of the theory is to discover properties of fields without relating to any specific example.
For many years, group theory and field theory and similar theories served as the standard-bearers of “pure” mathematics, until their uses in describing nature were discovered. Group theory and abstract field theory started with the work of Évariste Galois (1811–1832), as part of his attempt to identify and characterize the solutions of polynomial equations, that is, to find when and how many solutions exist to the numerical equation
p
(
x
) = 0, when
p
is a polynomial. Finding solutions to such equations was considered then, and to a great extent also today, applied mathematics. The abstract concepts of a group and a field were defined many years after Galois's time. Thus, group theory is a clear example of mathematics that developed from applications, and its definitions are based on known examples, from which the notion of abstract, “pure” mathematics as a subject was derived. From
there, as we saw in the section on groups of particles, applications, sometimes surprising ones, were found in totally different areas.
The day-by-day practice of mathematics sometimes stresses the theoretical aspect to the extent that it ignores what motivated the development of some mathematics and its possible applications. Influenced by developments in the study of the foundations of mathematics, a group of French mathematicians convened in the mid-1930s with the intention of systematically and rigorously recording and developing the mathematics that was known then, with the emphasis on mathematics for its own sake. They decided to publish a series of books, under the collective nom de plume Nicolas Bourbaki. The Bourbaki group was active for several decades and produced many books that had a significant impact on a sizable share of the mathematics community. No one questions the group's achievements in mathematics, but already in the course of its work, many disagreed with the approach that the group represented and championed, an approach that focused on mathematics for its own sake at the expense of its nonmathematical motivation and applications. The Bourbaki effect is still felt in certain circles, but today the approach that favors “mathematics shall dwell alone” is fading, and there is constantly growing recognition of the contribution of nonmathematical subjects to mathematics.
The following example describes mathematics that solved a very real problem and from which abstract mathematics developed along with largely applicable mathematics. The story starts with the accelerated development of steamships in the early nineteenth century. The engineering system used to stabilize the speed of the steamboats was what is still today known as the Watt regulator, named after the British scientist James Watt (1736–1819), whose name is also used for a unit of electrical energy. The steam engine would rotate, in addition to a propeller, a cylinder with two arms. When the engine was revolving rapidly, the centrifugal force raised the arms. When the revolutions were slow, the arms were in a low position. The arms were connected to a piston inside the cylinder, so that when the arms were raised, the piston blocked the flow of steam to the engine, and when the arms were low, this allowed a faster flow of steam to the
engine. Thus, a faster speed raised the arms, reduced the flow of steam, and lowered the speed. A slower speed lowered the arms, increasing the supply of steam and thus the speed. The system worked well, up to the stage where the engineers improved the quality of the pistons and the cylinders, and then the boats’ engines started to disintegrate.
The engineers did not manage to solve the problem and had no choice but to turn to James Clerk Maxwell, the famous scientist whose enormous contribution to science we have described previously (section 25), and he did indeed solve their problem. The first thing he did was to say to the engineers, and also to himself, that one must not trust human intuition. The action of the regulator that we described in the previous paragraph was based on the intuitive perception of the processes resulting from previous experience. In the absence of previous experience, intuition bases itself on understanding as fashioned by evolution. Steamships were not part of the process of evolution. Therefore, to check whether the intuition is right, mathematics must be used, just as the Greeks had taught the human race two thousand four hundred years earlier. Maxwell wrote down the differential equations that described the movement of the piston and showed where the intuition of the engineers had let them down. The failure lay in the fact that the mechanism described above related to the arms that regulated the steam being in a static state. The static intuition did not take into consideration the motion that the arms underwent in the transition from the low position to the high position and back again. The improvement of the piston made that movement faster, and that caused an overreaction and the destruction of the whole engine. The equations that Maxwell used identified the problem and led to the realization of how to solve it. He described his findings in a mathematical article published in 1868. Maxwell's applied research solved an engineering problem and, at the same time, opened up a new area of mathematics called control theory. Maxwell's colleagues, and prominent among them, his Cambridge associate Edward Routh, quickly entered the field and found mathematical criteria for the stability of general systems. Since then, the subject has been advancing in parallel in the areas of the applications of mathematics as well as of mathematics for its own sake. There are hardly any engineering systems in which control theory does not play a central role, and recently applications
of the theory have been found in economics and finance. The mathematicians who deal with control theory contribute both to the engineering aspect, where the applications of the theory are of greater interest, and also to the mathematical aspect itself, where the mathematics for its own sake plays a greater part.
The next fascinating example shows on the one hand how a mental challenge can lead to important results, and, on the other, the difference between a quick and “elegant” solution, for example, with the help of a trick, and a useful solution. To provide the background to this distinction we recall that the purpose of a proof in mathematics goes far beyond persuading the reader that the result is correct. The function of the proof is to explain why the result is as it is and to learn from it how to act in similar situations.
The Greeks were, apparently, the first to have studied the question of planning the route a body should take to get from one place to another in the shortest time. The usual formulation of the problem, known as the brachistochrone problem (from the Greek for “the shortest time”) is as follows.
Given points A and B in a vertical plane, as in the diagram, with A higher than B, plan the slide from A to B such that a ball falling without friction from A will reach B in the shortest time.
The Greeks thought that the optimal, that is, quickest, route was a straight line because that is the shortest distance between two points. That solution was rejected when the laws of motion were discovered, and in particular the law of falling bodies. Galileo proposed that the quickest route was a quadratic line, part of the circumference of a circle. He did not prove his claim completely, and the problem did not attract much further attention. In June 1696, Johann Bernoulli (1667–1748), brother of Jacob and father of Daniel,
both of whom we have already spoken, published a letter in which he stated that he had a complete and attractive solution to the problem and challenged the mathematics community to propose a solution before January of the following year. The letter, published in the scientific journal
Acta Eruditorum
, attracted the attention of mathematicians. Leibniz even asked Bernoulli to extend the deadline for submission of a solution. The extension was given, and in May 1697 solutions were published in the journal, including that of Bernoulli himself, another proposed by his oldest brother, Jacob, a solution by Leibniz (that was actually published elsewhere), and another by Newton. Other solutions by the French mathematician Guillaume François Antoine, marquis de L’Hôpital (1661–1704) and Ehrenfried von Tschirnhaus (1651–1708) were also published there.
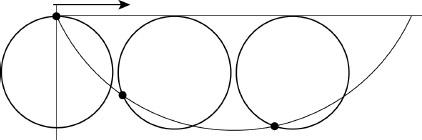
Johann's solution was indeed the shortest and most elegant. He suggested that although the problem relates to a falling ball, let us imagine that the path describes a beam of light that travels from A to B, passing through a medium in which the speed of light changes. The changes in its speed can be derived from the law of conservation of energy, with the potential energy of the difference in heights converted into kinetic energy, and with the conversion relative to the square of the speed. The beam of light, as was known in the days of Fermat, travels from one point to another in minimum time, and Snell's law (see section 21) defines the slope of the route along which the beam travels, which in our case is the slope of the path. As soon as the connection with Snell's law was established, prior knowledge could be employed, in particular, mathematics developed by Fermat and some of his contemporaries, to show that the path was cycloid, namely, the path traced by a point on the circumference of a circle, say, a round coin, that is rolling in a plane.
In contrast with Johann Bernoulli's trick of viewing the route as if it were the path of a beam of light, the solution proposed by his brother Jacob was long and complex and required laborious mathematical manipulations.
He started with a given line and asked what would happen if it were changed a little. If the original line is the solution, the change will result in the ball taking longer to reach its destination. If we calculate the difference in the times, we will obtain, using a method that today is relatively easy to describe but in those days was very complex, equations of a type that Jacob Bernoulli managed to solve, also relying on earlier studies. He also proved that the result was a cycloid.
The relations between the two brothers were not the best, to put it mildly; Johann even mocked his brother openly over his awkward solution. In response, Jacob used his method to solve other minimization problems that Johann could not solve using his trick or any other trick.