Out of My Later Years: The Scientist, Philosopher, and Man Portrayed Through His Own Words (6 page)
Authors: Albert Einstein

Considered formally, the admission of a coordinate system which is accelerated with respect to the original “inertial” coordinates means the admission of non-linear coordinate transformations, hence a mighty enlargement of the idea of invariance, i.e., the principle of relativity.
First, a penetrating discussion, using the results of the special theory of relativity, shows that with such a generalization the coordinates can no longer be interpreted directly as the results of measurements. Only the coordinate difference together with the field quantities which describe the gravitational field determine measurable distances between events. After one has found oneself forced to admit non-linear coordinate transformations as transformations between equivalent coordinate systems, the simplest demand appears to admit all continuous coordinate transformations (which form a group), i.e., to admit arbitrary curvilinear coordinate systems in which the fields are described by regular functions (general principle of relativity).
Now it is not difficult to understand why the general principle of relativity
(on the basis of the equivalence principle)
has led to a theory of gravitation. There is a special kind of space whose physical structure (field) we can presume as precisely known on the basis of the special theory of relativity. This is empty space without electromagnetic field and without matter. It is completely determined by its “metric” property: Let dx
0
, dy
0
, dz
0
, dt
0
be the coordinate differences of two infinitesimally near points (events); then
(1) ds
2
= dx
0
2
+ dy
0
2
+ dz
0
2
- c
2
dt
0
2
is a measurable quantity which is independent of the special choice of the inertial system. If one introduces in this space the new coordinates x
1
, x
2
, x
3
, x
4
through a general transformation of coordinates, then the quantity ds
2
for the same pair of points has an expression of the form
(2) ds
2
= ∑g
ik
dx
i
dx
k
(summed for i and k from 1 to 4)
where g
ik
= g
ki
. The g
ik
which form a “symmetric tensor” and are continuous functions of
x
1
. .
. x
4
then describe according to the “principle of equivalence” a gravitational field of a special kind (namely one which can be re transformed to the form (1)). From Riemann’s investigations on metric spaces the mathematical properties of this g
ik
field can be given exactly (“Riemann-condition”). However, what we are looking for are the equations satisfied by “general” gravitational fields. It is natural to assume that they too can be described as tensor-fields of the type g
ik
, which in general do
not
admit a transformation to the form (1), i.e., which do not satisfy the “Riemann condition,” but weaker conditions, which, just as the Riemann condition, are independent of the choice of coordinates (ie., are generally invariant). A simple formal consideration leads to weaker conditions which are closely connected with the Riemann condition. These conditions are the very equations of the pure gravitational field (on the outside of matter and at the absence of an electromagnetic field).
These equations yield Newton’s equations of gravitational mechanics as an approximate law and in addition certain small effects which have been confirmed by observation (deflection of light by the gravitational field of a star, influence of the gravitational potential on the frequency of emitted light, slow rotation of the elliptic circuits of planets—perihelion motion of the planet Mercury). They further yield an explanation for the expanding motion of galactic systems, which is manifested by the red-shift of the light omitted from these systems.
The general theory of relativity is as yet incomplete insofar as it has been able to apply the general principle of relativity satisfactorily only to gravitational fields, but not to the total field. We do not yet know with certainty, by what mathematical mechanism the total field in space is to be described and what the general invariant laws are to which this total field is subject. One thing, however, seems certain: namely, that the general principle of relativity will prove a necessary and effective tool for the solution of the problem of the total field.
IN ORDER TO UNDERSTAND the law of the equivalence of mass and energy, we must go back to two conservation or “balance” principles which, independent of each other, held a high place in pre-relativity physics. These were the principle of the conservation of energy and the principle of the conservation of mass. The first of these, advanced by Leibnitz as long ago as the seventeenth century, was developed in the nineteenth century essentially as a corollary of a principle of mechanics.
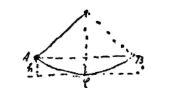
Drawing from Dr. Einstein’s manuscript.
Consider, for example, a pendulum whose mass swings back and forth between the points A and B. At these points the mass m is higher by the amount h than it is at C, the lowest point of the path (see drawing). At C, on the other hand, the lifting height has disappeared and instead of it the mass has a velocity v. It is as though the lifting height could be converted entirely into velocity, and vice versa. The exact relation would be expressed as mgh = m/2 v
2
, with g representing the acceleration of gravity. What is interesting here is that this relation is independent of both the length of the pendulum and the form of the path through which the mass moves.
The significance is that something remains constant throughout the process, and that something is energy. At A and at B it is an energy of position, or “potential” energy; at C it is an energy of motion, or “kinetic” energy. If this concept is correct, then the sum mgh + m v
2
/2 must have the same value for any position of the pendulum, if h is understood to represent the height above C, and v the velocity at that point in the pendulum’s path. And such is found to be actually the case. The generalization of this principle gives us the law of the conservation of mechanical energy. But what happens when friction stops the pendulum?
The answer to that was found in the study of heat phenomena. This study, based on the assumption that heat is an indestructible substance which flows from a warmer to a colder object, seemed to give us a principle of the “conservation of heat.” On the other hand, from time immemorial it has been known that heat could be produced by friction, as in the fire-making drills of the Indians. The physicists were for long unable to account for this kind of heat “production.” Their difficulties were overcome only when it was successfully established that, for any given amount of heat produced by friction, an exactly proportional amount of energy had to be expended. Thus did we arrive at a principle of the “equivalence of work and heat.” With our pendulum, for example, mechanical energy is gradually converted by friction into heat.
In such fashion the principles of the conservation of mechanical and thermal energies were merged into one. The physicists were thereupon persuaded that the conservation principle could be further extended to take in chemical and electromagnetic processes—in short, could be applied to all fields. It appeared that in our physical system there was a sum total of energies that remained constant through all changes that might occur.
Now for the principle of the conservation of mass. Mass is defined by the resistance that a body opposes to its acceleration (inert mass). It is also measured by the weight of the body (heavy mass). That these two radically different definitions lead to the same value for the mass of a body is, in itself, an astonishing fact According to the principle—namely, that masses remain unchanged under any physical or chemical changes—the mass appeared to be the essential (because unvarying) quality of matter. Heating, melting, vaporization, or combining into chemical compounds would not change the total mass.
Physicists accepted this principle up to a few decades ago. But it proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat now proceeded to swallow that of the conservation of mass—and holds the field alone.
It is customary to express the equivalence of mass and energy (though somewhat inexactly) by the formula E=mc
2
, in which c represents the velocity of light about 186,000 miles per second. E is the energy that is contained in a stationary body; m is its mass. The energy that belongs to the mass m is equal to this mass, multiplied by the square of the enormous speed of light—which is to say, a vast amount of energy for every unit of mass.
But if every gram of material contains this tremendous energy, why did it go so long unnoticed? The answer is simple enough: so long as none of the energy is given off externally, it cannot be observed. It is as though a man who is fabulously rich should never spend or give away a cent; no one could tell how rich he was.
Now we can reverse the relation and say that an increase of E in the amount of energy must be accompanied by an increase of E/c
2
in the mass. I can easily supply energy to the mass—for instance, if I heat it by 10 degrees. So why not measure the mass increase, or weight increase, connected with this change? The trouble here is that in the mass increase the enormous factor c
2
occurs in the denominator of the fraction. In such a case the increase is too small to be measured directly; even with the most sensitive balance.
For a mass increase to be measurable, the change of energy per mass unit must be enormously large. We know of only one sphere in which such amounts of energy per mass unit are released: namely, radioactive disintegration. Schematically, the process goes like this: An atom of the mass M splits into two atoms of the mass M′ and M″, which separate with tremendous kinetic energy. If we imagine these two masses as brought to rest—that is, if we take this energy of motion from them—then, considered together, they are essentially poorer in energy than was the original atom. According to the equivalence principle, the mass sum M′ + M″ of the disintegration products must also be somewhat smaller than the original mass M of the disintegrating atom—in contradiction to the old principle of the conservation of mass. The relative difference of the two is on the order of
1/10
of one percent.
Now, we cannot actually weigh the atoms individually. However, there are indirect methods for measuring their weights exactly. We can likewise determine the kinetic energies that are transferred to the disintegration products M′ and M″. Thus it has become possible to test and confirm the equivalence formula. Also, the law permits us to calculate in advance, from precisely determined atom weights, just how much energy will be released with any atom disintegration we have in mind. The law says nothing, of course, as to whether—or how—the disintegration reaction can be brought about
What takes place can be illustrated with the help of our rich man. The atom M is a rich miser who, during his life, gives away no money
(energy).
But in his will he bequeaths his fortune to his sons M′ and M″, on condition that they give to the community a small amount, less than one thousandth of the whole estate
(energy or mass).
The sons together have somewhat less than the father had
(the mass sum M
′ + M″
is somewhat smaller than the mass M of the radioactive atom).
But the part given to the community, though relatively small, is still so enormously large (
considered as kinetic energy)
that it brings with it a great threat of evil. Averting that threat has become the most urgent problem of our time.
What Is the Theory of Relativity?
I GLADLY ACCEDE to the request of your colleague to write something for
The Times
on relativity. After the lamentable breakdown of the old active intercourse between men of learning, I welcome this opportunity of expressing my feelings of joy and gratitude towards the astronomers and physicists of England. It is thoroughly in keeping with the great and proud traditions of scientific work in your country that eminent scientists should have spent much time and trouble, and your scientific institutions have spared no expense, to test the implications of a theory which was perfected and published during the War in the land of your enemies. Even though the investigation of the influence of the gravitational field of the sun on light rays is a purely objective matter, I cannot forbear to express my personal thanks to my English colleagues for their work; for without it I could hardly have lived to see the most important implication of my theory tested.
