Secrets of Antigravity Propulsion (49 page)

12.4 • THE CORNILLE-NAUDIN PENDULUM EXPERIMENTS
In 1996, physicist Patrick Cornille constructed a double-ball pendulum similar to the one Brown had tested in his 1920s experiments.
10,
11,
12
He suspended a pair of aluminum spheres, each weighing 500 grams, from two nylon lines and applied between 30 and 50 kilovolts DC to the spheres through two wires secured to these lines (figure 12.8).
Each high-voltage feed wire measured half a millimeter (20 mils) in diameter.
Each time he turned on his power supply, the pendulum would swing in the direction of its positively charged sphere, in apparent violation of Newton’s third law of motion.
That is, Brown’s classic pendulum experiment apparently violates the law of conservation of momentum.
At 50 kilovolts, the pendulum was acted on by a force of 3.5 grams.
Curiously, Cornille found that the effect occurred only when he used bare feed wires, as opposed to insulated feed wires.
He found that the bare feed wires were able to emit a 1.5-milliamp ion-leakage current through the air.
This demonstrates that the emission of charges into the atmosphere plays an important role.
He showed that the conventional ion wind theory, however, failed to explain the pendulum’s movement, since ions attracted to the opposite electrode would impact with a force that was two orders of magnitude too small.
Also, such a mechanism would not explain his finding that the developed force increased as a moderate function of the pendulum mass, ~m
0.5
.

Figure 12.8.
The electrogravitic pendulum experiment carried out by Patrick
Cornille in July 1996.
High-voltage DC is fed to the spheres via the suspension
wires.
(Photo courtesy of P.
Cornille)
Cornille theorized that the leakage current was somehow related to the thrust effect, but offered no clear explanation.
As we shall see below, the observed thrust effect is most likely electrogravitic, arising from the ion space charge established in the air.
For example, Cornille estimates that his feed wires would have been emitting ions at the rate of about 10
16
ions per second, since their ion-leakage current amounted to 1.5 milliamperes.
13
Consequently, they would have been generating about 5
× 10
13
ions per second per centimeter of wire length.
Let us suppose that this built up space charges of the order of 10
13
ions per square centimeter along the wires.
Here, we make a very rough estimate, adopting a value similar to that given in Supplement B of the 1960 “Electrohydrodynamics” report for the ion-space charge developed around Brown’s vertical-thrust electrokinetic apparatus.
14
In the case of Cornille’s experiment, the volume of air lying within 5 centimeters of each wire would have contained on the order of 10
17
ions.
This would be more than 10,000 times the surface charge that would have accumulated on the surface of the feed wires and the pendulum spheres, which according to Cornille’s estimate would have been around 3.5
× 10
12
ions.
15
So we see that the electrogravitic force would be substantially enhanced by allowing a leakage current to create ions in the vicinity of the feed wires.
In the case in which the wires were insulated, a small amount of ion leakage would have been present between the pendulum’s spheres, but according to subquantum kinetics, the gravity gradient created between the resulting positive and negative-ion space charge would have existed between the spheres but would not have intercepted the spheres themselves (see figure 12.9).
Only the lightweight plastic spacer between the spheres would have been affected by this field, so the electrogravitic thrust on the pendulum would have been very slight.
Also, since the spheres that make up the bulk of the pendulum mass would have lain on the outer sides of the ion clouds, they would have experienced a thrust in a direction opposite to the central thrust vector acting on the insulating spacer.
Furthermore, since the ion-leakage current between the spheres was relatively low at 3 microamps, or about five hundred times less than the ion leakage produced when the pendulum was tested with bare feed wires, the spheres would have emitted only a small number of ions.
Hence, the induced gravity gradients would have been quite minimal.
In summary, it is not surprising that Cornille observed no pendulum movement.
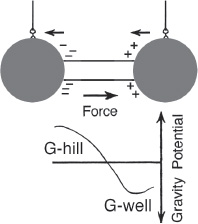
Figure 12.9.
Chart of the gravity gradient in
the Patrick Cornille pendulum experiment
when the high-voltage feed wires are
insulated.
(P.
LaViolette,
© 2006)
However, in the case in which the pendulum was tested with bare feed wires, most of the ions would have been released along the length of the wires at a considerable distance from the pendulum masses.
The ions released from the lower extremity of the feed wires, where the wires attach to the spheres, would have had the greatest influence on the pendulum.
Their ion clouds would have been separated by a sufficient distance so that their induced gravity field gradient would have intercepted part of the pendulum masses (see figure 12.10).
The G-on fluxes coming from more remote ion space charges located farther up the feed wire may also have had some effect by enhancing the magnitude of the gravity potential hills and wells being generated in the vicinity of the pendulum.
I would like to emphasize, again, that the electrostatically charged pendulum experiences an applied gravitational thrust in the absence of any so-called space-time warping.
The general relativistic concept of gravitational space-time warping is a fiction.
Understanding electrogravitics requires that we dispense with such outdated ideas and adopt new concepts such as those proposed in subquantum kinetics.
Namely, gravity potential gradients are understood to be concentration gradients created in an ether that occupies a Euclidean space.
Such gradients cause movement by altering the etheric reactions that are continually regenerating the fields of the propelled object’s constituent subatomic particles.
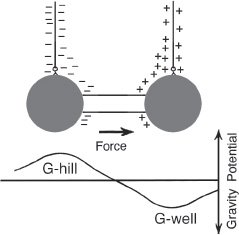
Figure 12.10.
Chart of the gravity
gradient in the Patrick Cornille
pendulum experiment when the
high-voltage feed wires are bare.
(P.
LaViolette, © 2006)
French researcher Jean-Louis Naudin duplicated Cornille’s pendulum experiment and found that the pendulum moved even when the vertical ion-emitting feed wires were detached from the metal spheres and supported at the distal ends of the spheres by means of insulating polystyrene blocks,
16
so he demonstrated that charging of the spheres was not crucial to the effect.
Like Cornille, he found that the magnitude of the force increased as the mass of the spheres increased, indicating the presence of an unconventional gravitational effect.
These results support the electrogravitic theory suggested above as an interpretation of Cornille’s pendulum experiment and also suggested earlier in the analysis of Brown’s electric discs.
Naudin was generating positive and negative ion clouds on either side of the test mass spheres and, according to the subquantum kinetic theory, a gravity potential gradient would have been generated between these charged ion poles.
The test masses, which were situated in the midst of this electric and gravity potential field gradient, then moved in the direction of the outlying gravity potential well, that is, the outlying positive ion cloud (see figure 12.11).
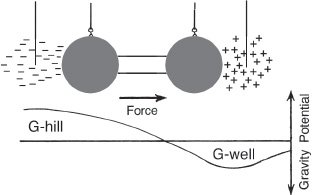
Figure 12.11.
Chart of the proposed gravity gradient generated in Jean-Louis Naudin’s modification of Patrick Cornille’s pendulum experiment.
(P.
LaViolette, © 2006)
Naudin also tested the pendulum by energizing it through feed wires that were insulated and through which a 0.5-milliamp ionization current was allowed to flow between the two balls.
As in Cornille’s experiment with insulated feed wires, Naudin’s experiment provided no observable pendulum movement.
This resolved the question raised by Naudin as to whether current flow might play a crucial role.
It showed that it is not the current flow itself that is important, but rather the location of ion discharge in relation to the spherical masses.
12.5 • LIFTER RESEARCH
During the 1970s, Jeff Cameron, an engineer working in Huntsville, Alabama, was researching a laser preionizer, a triangular high-voltage filament used to ionize the lasing medium in a gas laser, when he observed unusually strong forces deforming the preionizer element.
This led him later to build and test a large-scale replica.
It was similar to the parallel slat thruster described in Brown’s 1960 electrokinetic apparatus patent and to the thruster built by Turman, but was much lighter in weight and had its slats arranged to form a triangle.
This electrostatic thrust device, which has since come to be called a
lifter
, consisted of three vertical aluminum-foil fins connected to form a larger triangular structure with a thin wire supported horizontally above the fins.
The upper edge of each fin facing the wire was made to have a rounded contour.
When charged with 30 kilovolts, the device was observed to levitate.
After Cameron posted his findings on the Internet, Naudin tested a modified version of Cameron’s lifter that used a 2-mil-diameter (0.05-millimeter) emitter wire and a central baffle to duct the airflow (figure 12.12).
17
Interestingly, this wire diameter comes close to the 1mil diameter that Brown used in his electrokinetic disc experiments.
The lower-fin electrodes in Naudin’s device were 1.5 centimeters wide and 30 centimeters long, and had a rounded upper edge.
The wire was suspended 7 centimeters above the fin.
His device was able to lift its own weight of 4 grams plus an added 2-gram weight when energized with 37 kilovolts.
After Naudin posted the construction plans for building a lifter on his website, hundreds of hobbyists began duplicating the experiment and testing their own versions.
The ensuing frenzy even attracted media attention.
Lifter researcher Tim Ventura played a central role in catalyzing this widespread activity that even developed into competitions to see who could build and levitate the heaviest lifter.
Ventura’s website (
www.americanantigravity.com
) is a good resource for those interested in ongoing lifter research.
Experimenters found that they could obtain even more spectacular results when they combined many triangular lifters into a single structure.
Some have been made that weigh as much as 250 grams, which includes the weight of a 60-gram payload.
An image of one such multielement lifter in flight is shown in figure 12.13.
Saviour, a French researcher, found that he could improve the thrust of the lifter by using a nichrome emitter wire heated with a current from a 12-volt power supply.
Thus, he rediscovered the phenomenon Turman had discovered in the early 1970s in carrying out his brass slat lifter experiment.
The heated wire was able to emit more ions at a given voltage potential.
Again, these findings confirm ideas hinted at in Brown’s writings, which indicate that methods of encouraging ion emission from the wire electrode would increase the resulting thrust.
Although ions are important in producing the lifter’s thrust, its thrust is not due to ion wind effects, that is, forces arising from the recoil or impact of ions on the electrodes.
Such mechanical forces have been shown to fall short by several orders of magnitude in accounting for the observed lift.

Figure 12.12.
A lifter built and tested by Jean-Louis Naudin.
(Photo courtesy of J.-L.
Naudin, from his website,
http://jnaudin.free.fr/
)

Figure 12.13.
A multielement lifter in flight.
(Photo courtesy of Tim Ventura)
As Turman discovered in his cylindrical, asymmetrical capacitor experiments, so, too, lifter researchers found that they could get lifters to work by charging the wire to either a positive or a negative potential.
Since the lifters are made of extremely lightweight materials, such as aluminum foil and plastic soda straws, electrogravitic forces would not play an important role in producing their thrust.
Rather, the thrust is most likely attributable to unbalanced electrostatic forces (see text box below).
Others, such as Naudin, have given similar explanations.
18
Unbalanced Ionic Electrostatic Forces Acting on a Lifter
Consider a case in which the lifter’s emitter wire is positively charged.
The positive-ion cloud generated around the wire would be displaced below the wire since the field would be stronger on the lower side of the wire facing the underlying negative electrode.
This downward-displaced cloud would produce a net-upward electrostatic repulsive force on the adjacent wire.
Since the field is very nonlinear and concentrated near the wire, this upward-repulsive force would be comparably strong.
Also, the upper edge of the negative electrode would experience an upward force because it is electrostatically attracted to the positive-ion cloud.
The lower negative-ion cloud would not be as extensive as the upper positive-ion cloud for a number of reasons.
First, negative ions would be emitted from the negative electrode at a lower rate because of its lower electric field gradient.
Second, positive ions brought downward by the ion wind would neutralize many of the negative ions in the air and would also impinge on the negative electrode to neutralize negative charges on the electrode.
Furthermore, the mixture of positive and negative ions in the vicinity of the negative electrode would tend to screen the negative-ion space charge.
Any net-negative-ion charge present in the vicinity of the negative electrode would direct its force nearly horizontal to the electrode fin, pushing toward the fin from either side.
In addition, the downward ion-wind flow would cause a modest negative-ion space charge to build up below the negative electrode, and this would tend to produce an upward-directed repulsion force on that electrode.
All of these forces together would cause the entire lifter structure to levitate.
If the wire was instead negatively charged and the fins were positively charged, unbalanced electrostatic forces would again produce lift.
Although an ion wind continually rushes downward, that is, in the direction of lower electric field intensity, these ions are continually replaced by newly emitted ions, so these ion space charges will always be present to exert their upward forces on the wire and fin.
Any means of encouraging greater ion emission from the upper electrode would increase the ion-space charge in the vicinity of the wire as well as the upward repulsive electrostatic forces, thereby improving lift.
Such electrostatic forces would produce an upward thrust regardless of the applied field polarity.
Similar unbalanced electrostatic forces would account for the thrust developed by Turman’s cylinders.
Electrogravitic forces become more significant in the electrokinetic pendulum experiments of Brown and Cornille, which involve the propulsion of a heavy mass.
Accordingly, we find in such cases that the apparatus always moves toward its positive pole.
However, the explanation of electrostatic forces produced by ion-space charges does not tell the full story of what is happening in the lifter.
For example, Purdue University researcher William Stein carried out a lifter test in which a 12-centimeter-long lifter was energized with 17 kilovolts in a high vacuum.
19
Although the lifter was unable to support its weight, it reportedly produced a levitating thrust of 0.3 millinewtons.
Stein’s test would indicate that with ion emission essentially eliminated, a lifter is still able to generate a measurable thrust, which would be about 12 percent of what it would generate if allowed to operate in air.
*37
Hungarian researcher Zoltan Losonc has done a computer analysis of the electrostatic forces that a lifter’s charged electrodes would generate when electrified in a vacuum.
He has concluded that no lift force should be produced and, hence, that some exotic principle must be operating to explain the results of the Purdue vacuum test.
20
The question remains as to whether Stein’s measurements may have been influenced by electrostatic forces developed between his lifter element and the vacuum chamber walls.
His 12-centimeter-long lifter should have weighed less than 2 grams, as compared with the arcuate discs that Brown vacuum tested, which ranged in weight from 17 to 125 grams.
Naudin has also performed tests that, like Stein’s, suggest the lifter may be generating a force in the direction of its smaller electrode in the absence of ion electrostatic forces.
He placed plastic soda straws over a lifter’s emitter wires to prevent its emission of ions and found that the lifter still produced a measurable lifting force.
21
He also found that his lifter produced a measurable thrust even when enclosed in a plastic bag, thereby containing its ion wind.
Naudin has posted only general information about this on the Internet, leaving some questions unanswered, such as whether the force he measured may have been due to electrostatic attraction between his lifter and the beam balance on which it was placed.
So, as with Stein’s results, it may be premature to draw any conclusions.
If the thrust in a vacuum is observed only when the wire is positively charged, then perhaps the force could be explained as a manifestation of the Biefeld-Brown effect, that is, an electrogravitic force acting on the lifter’s mass.
However, because of the absence of any massive dielectric element between the lifter electrodes, it is unlikely that an appreciable electrogravitic effect would be present.
Unclassified public research on electrogravitics research is, for the most part, being conducted by independent researchers, some of whom have been mentioned above.
With few exceptions, no similar research is being conducted at universities or government research institutions.
Clearly, the science and engineering establishment needs to take a serious interest in conducting additional electrogravitics research before the secrets of field-effect propulsion, currently locked away in black R&D programs, becomes openly applied to make mankind’s dream of antigravity a reality.
