SS Brotherhood of the Bell: The Nazis’ Incredible Secret Technology (36 page)
Read SS Brotherhood of the Bell: The Nazis’ Incredible Secret Technology Online
Authors: Joseph P. Farrell

In case this is not clear enough, Bearden, who has a bachelor of science degree in mathematics, a master of science degree in engineering, and a PhD in science, puts the miserable state of “public consumption physics” and its electrodynamics in no uncertain terms:
There is not now, and there never has been, a single electrical engineering department, electrical engineering professor, or electrical engineering textbook that teaches what powers an electrical circuit. Yet the basis for it has clearly been in particle physics since 1957, as certified by the award of the Nobel Prize to Lee and Yang. What powers every electrical circuit and system is the broken symmetry of the primary power system’s source charges and source dipole (i.e., the broken symmetry of the opposite charges on the ends of the dipole) in its fierce energy exchange with the seething vacuum, once that dipole has been made. … Further, any dipole will freely extract (electromagnetic) energy from the vacuum, convert it into real, usable, observable (electromagnetic) energy, and pour out real, usable (electromagnetic) energy continuously and indefinitely, so long as the dipole remains intact.
31
Or to put it more simply, all electromagnetic devices and circuits “are already powered – though in an inappropriate fashion – by (electromagnetic) energy freely extracted from the vacuum.”
32
All electrical circuits, in other words, are already “zero point energy” or “quantum potential” devices.
33
They are just massively inefficient ones for reasons that will be seen shortly.
Since classical electrodynamics viewed charge in a most unscientific manner as a “perpetual motion machine” getting energy from literally nowhere, the next error inevitably followed: electrical circuits and electromagnetic systems were
closed
systems.
But how, then, would classical electrodynamics explain the Coler coil, the curious circuit reproduced in
Reich of the Black Sun
?
34

The Coler Coil
As mentioned there, this odd hexagonal arrangement of coils and magnets had
absolutely no source of power
and yet it managed to
produce
power.
Clearly, this circuit, understood in the wider context of the other issues examined in this chapter, would have spurred the German scientists to seek an explanation within the context of the ideologically approved physics of the Nazi regime, i.e., in quantum mechanics and its prediction of a vacuum flux, or “zero point energy.” In understanding such a circuit, in understanding
any
circuit, one will thus find it necessary – if one is to avoid the “perpetual motion machine” of standard electrodynamics – “to think in terms of the
supersystem
, defined as having three components, which are (i) the physical power system itself, (ii) the active local vacuum, and (iii) the active local curvatures of spacetime.”
35
Any electrical circuit is thus not a
closed
system but an
open
system.
36
We now have the first three fundamental components of scalar physics and technologies:
(1) the medium, aether substrate, or “active local vacuum”,
(2) the local curved dynamic of space,
37
and
(3) an understanding of circuits as
open
systems, rather than closed perpetual motion machines.
Moreover, as the Coler Coil seems to imply,
some
circuits are more efficient at transducing this “active vacuum” energy than others, and one may reasonably assume, therefore, that this efficiency is a function of its circuit parameters, i.e., of its
geometry
and “
electrical topology,”
of its
shape.
b. What the Soviets (and Nazis) Found in their Scavenger Hunt: E.T. Whittaker’s Decomposition of Scalar Potentials into Bi-Directional Longitudinal Waves
So, with these observations in mind, it is time to ask the important question: What exactly did the Soviets
find
during their scavenger hunt? And more to the point, what might the Germans have concluded and carefully classified from their examination of the Coler Coil? To answer this, it is necessary to take up Bearden’s reconstruction of the history of scalar weapons where we left it off.
Bearden maintains that in scouring the West’s scientific journals the Soviets would have come across three relatively obscure, highly mathematical, entirely pre-relativistic, and
immensely unusual
papers. Two of them were by the well-known mathematician and theoretical physicist E.T. Whittaker, and one was by a physicist named Barus. Of the three, the Whittaker papers are breathtaking in their implications, not the least of which because they can be made to work within the context of the later-developed quantum theory.
The first paper, a lengthy and highly mathematical tome, is a masterpiece whose full implications – in spite of its benign and somewhat intimidating title “On the partial differential equations of mathematical physics” – are spelled out by Whittaker in the conclusion of the paper(I have italicized the significant portions that bear directly on Bearden’s analysis which follows):
It is clear from the foregoing that the field of force due to a gravitating body can be analyzed, by a “spectrum analysis” as it were, into an infinite number of constituent fields;
and although the whole field of force does not vary with time, yet
each of the constituent fields is of an undulatory character, consisting of a simple wave-disturbance propagated with uniform velocity
…
. In each of these constituent fields the potential will be constant along each wave-front, and consequently the gravitational force in each constituent field will be perpendicular to the wave-front,
i.e., the waves will be longitudinal.
38
The significance of this short paragraph may be missed unless one remembers that E.T. Whittaker was also a physicist who believed ardently in the
aether
, i.e., in a medium or mechanism of electromagnetic energy propagation. Indeed, he is the same Whittaker who wrote a classic history of the concept of the aether. Note also that this paper was originally published
in Germany
, and therefore, the Germans could hardly have been unaware of its existence or of its importance as a
non-relativistic
physics as they sought to explain the curious anomalies of the Coler Coil or their late war radar experiments. Indeed, their experiments with radar, and even the Bell itself, are evidence that they were pursuing this “scalar physics” with a vengeance.
To understand what Bearden means by “scalar” waves in the medium or vacuum, we must now go further into the history of where public consumption physics went wrong. According to Bearden, it began to make its first massive wrong turn after Maxwell. Maxwell first formulated his equations in a mathematical language all but extinct today, a mathematical language called quaternion geometry. This mathematical language differs significantly from the standard “linear algebra,” “tensor calculus” and “vector analysis” in which the standard electromagnetic theory is usually couched in textbooks and physics lectures. In short, the equations one learns in physics textbooks and physics courses today as Maxwell’s equations are
not
Maxwell’s original equations! They are
edited
equations. But to understand what effect this simple change of mathematical language – from quaternions to vector analysis – had on physics, we need to understand a few simple concepts.
First, there are two type of effects that electromagnetic fields can have on charged particles: (1) translation, and (2) stress. There are two types of translation, or movement. The first type is simple translation in a straight line, producing the electrical, or “E” field itself. The second type of movement is that of a spiral, mathematically symbolized as the “B” field. We will not be dealing with the “B” field immediately.
Now let us assume there are two vectors, E1 and E2, acting upon a particle as shown:

The result is a translation in the direction of vector E3 as the two vectors are added together to get a result, which is called aptly enough, a “resultant” vector. Thus, in systems where a large number of translation vectors are involved, “the entire system can be replaced by a single vector,” the resultant, which describes the
actual
translation that results from the original vectors.
39
Now observe that if no translation occurs, the resultant is a “zero vector.” However, one must always recall that one is dealing with
geometry
and not simply
mathematics or numbers.
One can therefore envision a multitude of multivector systems resulting in a zero translation vector, and yet
which have profoundly different internal stresses and geometries:
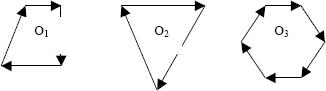
If one were trained to think only in terms of the conventions of linear algebra to replace multivector systems with a resultant vector, then in each of the three cases or systems above, one will replace the entire system with a
zero resultant vector.
This means that the
internal stresses of the systems and their rotational characteristics – each obviously quite different – are all replaced by a zero vector, and thus the three systems are erroneously reduced to physical equivalence by a mathematical convention!
Now we are in a position to see what a scalar is, and why Maxwell deliberately chose quaternion geometry to write his equations, for he had in mind when he did so precisely the types of physical
stress
situations that are simply represented by the vortices in the above diagram.
In standard linear algebra, each of the arrows in the above system would be mathematically represented like this:
v(vector) = ai + bj + ck.
Thus, if the total sum of all such vectors is no translation, then one will replace all such mathematical expressions with a zero vector. But as we have seen, each of these systems contains an internal rotation or stress, so
something
remains. The question is, how to represent it mathematically?
In quaternion geometry, a quaternion is simply a “scalar” plus a “vector,” and a “scalar” is simply a
pure magnitude
, a “number” that has no
direction
. It simply “is.” Thus, a quaternion (q) is a scalar(s) plus a vector (v):
q = s + v
Substituting our previous expression of a vector into this, we get
q = s + ai + bj + ck.
Thus, for the hexagonally shaped system above, one would have six different expressions resembling q = s + ai + bj + ck. Now imagine we multiply each of these vectors. According to the special rules in linear algebra for multiplying such things, we know that zero times zero is zero. So in linear algebra one would end up with nothing once again, a zero vector, since no translation has occurred. But in
quaternion geometry the scalars, which are
not
zero, all multiply, and give – according to the rules of quaternion multiplication – the following result:
