Superintelligence: Paths, Dangers, Strategies (47 page)
Read Superintelligence: Paths, Dangers, Strategies Online
Authors: Nick Bostrom
Tags: #Science, #Philosophy, #Non-Fiction

A race dynamic exists when one project fears being overtaken by another. This does not require the actual existence of multiple projects. A situation with only one project could exhibit a race dynamic if that project is unaware of its lack of competitors. The Allies would probably not have developed the atomic bomb as quickly as they did had they not believed (erroneously) that the Germans might be close to the same goal.
The severity of a race dynamic (that is, the extent to which competitors prioritize speed over safety) depends on several factors, such as the closeness of the race, the relative importance of capability and luck, the number of competitors, whether competing teams are pursuing different approaches, and the degree to which projects share the same aims. Competitors’ beliefs about these factors are also relevant. (See
Box 13
.)
In the development of machine superintelligence, it seems likely that there will be at least a mild race dynamic, and it is possible that there will be a severe race dynamic. The race dynamic has important consequences for how we should think about the strategic challenge posed by the possibility of an intelligence explosion.
The race dynamic could spur projects to move faster toward superintelligence while reducing investment in solving the control problem. Additional detrimental effects of the race dynamic are also possible, such as direct hostilities between competitors. Suppose that two nations are racing to develop the first superintelligence, and that one of them is seen to be pulling ahead. In a winner-takes-all situation, a lagging project might be tempted to launch a desperate strike against its rival rather than passively await defeat. Anticipating this possibility, the frontrunner might be tempted to strike preemptively. If the antagonists are powerful states, the clash could be bloody.
34
(A “surgical strike” against the rival’s AI project might risk triggering a larger confrontation and might in any case not be feasible if the host country has taken precautions.
35
)
Consider a hypothetical AI arms race in which several teams compete to develop superintelligence.
32
Each team decides how much to invest in safety—knowing that resources spent on developing safety precautions are resources not spent on developing the AI. Absent a deal between all the competitors (which might be stymied by bargaining or enforcement difficulties), there might then be a risk-race to the bottom, driving each team to take only a minimum of precautions.
One can model each team’s performance as a function of its capability (measuring its raw ability and luck) and a penalty term corresponding to the cost of its safety precautions. The team with the highest performance builds the first AI. The riskiness of that AI is determined by how much its creators invested in safety. In the worst-case scenario, all teams have equal levels of capability. The winner is then determined exclusively by investment in safety: the team that took the fewest safety precautions wins. The Nash equilibrium for this game is for every team to spend nothing on safety. In the real world, such a situation might arise via a
risk ratchet
: some team, fearful of falling behind, increments its risk-taking to catch up with its competitors—who respond in kind, until the maximum level of risk is reached.
The situation changes when there are variations in capability. As variations in capability become more important relative to the cost of safety precautions, the risk ratchet weakens: there is less incentive to incur an extra bit of risk if doing so is unlikely to change the order of the race. This is illustrated under various scenarios in
Figure 14
, which plots how the riskiness of the AI depends on the importance of capability. Safety investment ranges from 1 (resulting in perfectly safe AI) to 0 (completely unsafe AI). The
x
-axis represents the relative importance of capability versus safety investment in determining the speed of a team’s progress toward AI. (At 0.5, the safety investment level is twice are important as capability; at 1, the two are equal; at 2, capability is twice as important as safety level; and so forth.) The
y
-axis represents the level of AI risk (the expected fraction of their maximum utility that the winner of the race gets).
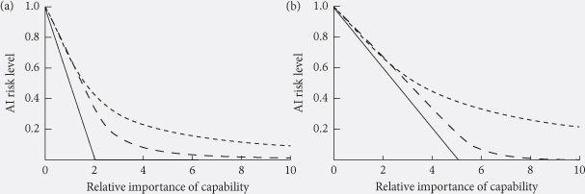
Figure 14
Risk levels in AI technology races. Levels of risk of dangerous AI in a simple model of a technology race involving either (a) two teams or (b) five teams, plotted against the relative importance of capability (as opposed to investment in safety) in determining which project wins the race. The graphs show three information-level scenarios: no capability information (straight), private capability information (dashed), and full capability information (dotted).
We see that, under all scenarios, the dangerousness of the resultant AI is maximal when capability plays no role, gradually decreasing as capability grows in importance.
Another way of reducing the risk is by giving teams more of a stake in each other’s success. If competitors are convinced that coming second means the total loss of everything they care about, they will take whatever risk necessary to bypass their rivals. Conversely, teams will invest more in safety if less depends on winning the race. This suggests that we should encourage various forms of cross-investment.
The greater the number of competing teams, the more dangerous the race becomes: each team, having less chance of coming first, is more willing to throw caution to the wind. This can be seen by contrasting
Figure 14
a (two teams) with
Figure 14
b (five teams). In every scenario, more competitors means more risk. Risk would be reduced if teams coalesce into a smaller number of competing coalitions.
Is it good if teams know about their positions in the race (knowing their capability scores, for instance)? Here, opposing factors are at play. It is desirable that a leader knows it is leading (so that it knows it has some margin for additional safety precautions). Yet it is undesirable that a laggard knows it has fallen behind (since this would confirm that it must cut back on safety to have any hope of catching up). While intuitively it may seem this trade-off could go either way, the models are unequivocal: information is (in expectation) bad.
33
Figures 14
a and
14
b each plot three scenarios: the straight lines correspond to situations in which no team knows any of the capability scores, its own included. The dashed lines show situations where each team knows its own capability only. (In those situations, a team takes extra risk only if its capability is low.) And the dotted lines show what happens when all teams know each other’s capabilities. (They take extra risks if their capability scores are close to one another.) With each increase in information level, the race dynamic becomes worse.
Scenarios in which the rival developers are not states but smaller entities, such as corporate labs or academic teams, would probably feature much less direct destruction from conflict. Yet the overall consequences of competition may be almost as bad. This is because the main part of the expected harm from competition stems not from the smashup of battle but from the downgrade of precaution. A race dynamic would, as we saw, reduce investment in safety; and conflict, even if nonviolent, would tend to scotch opportunities for collaboration, since projects would be less likely to share ideas for solving the control problem in a climate of hostility and mistrust.
36
Collaboration thus offers many benefits. It reduces the haste in developing machine intelligence. It allows for greater investment in safety. It avoids violent conflicts. And it facilitates the sharing of ideas about how to solve the control problem. To these benefits we can add another: collaboration would tend to produce outcomes in which the fruits of a successfully controlled intelligence explosion get distributed more equitably.
That broader collaboration should result in wider sharing of gains is not axiomatic. In principle, a small project run by an altruist could lead to an outcome where the benefits are shared evenly or equitably among all morally considerable beings. Nevertheless, there are several reasons to suppose that broader collaborations, involving a greater number of sponsors, are (in expectation) distributionally superior. One such reason is that sponsors presumably prefer an outcome in which they themselves get (at least) their fair share. A broad collaboration then means that relatively many individuals get at least their fair share, assuming the project is successful. Another reason is that a broad collaboration also seems likelier to benefit people outside the collaboration. A broader collaboration contains more members, so more outsiders would have personal ties to somebody on the inside looking out for their interests. A broader collaboration is also more likely to include at least some altruist who wants to benefit everyone. Furthermore, a broader collaboration is more likely to operate under public oversight, which might reduce the risk of the entire pie being captured by a clique of programmers or private investors.
37
Note also that the larger the successful collaboration is, the lower the costs to it of extending the benefits to all outsiders. (For instance, if 90% of all people were already inside the collaboration, it would
cost them no more than 10% of their holdings to bring all outsiders up to their own level.)
It is thus plausible that broader collaborations would tend to lead to a wider distribution of the gains (though
some
projects with few sponsors might also have distributionally excellent aims). But why is a wide distribution of gains desirable?
There are both moral and prudential reasons for favoring outcomes in which everybody gets a share of the bounty. We will not say much about the moral case, except to note that it need not rest on any egalitarian principle. The case might be made, for example, on grounds of fairness. A project that creates machine superintelligence imposes a global risk externality. Everybody on the planet is placed in jeopardy, including those who do not consent to having their own lives and those of their family imperiled in this way. Since everybody shares the risk, it would seem to be a minimal requirement of fairness that everybody also gets a share of the upside.
The fact that the total (expected) amount of good seems greater in collaboration scenarios is another important reason such scenarios are morally preferable.
The prudential case for favoring a wide distribution of gains is two-pronged. One prong is that wide distribution should promote collaboration, thereby mitigating the negative consequences of the race dynamic. There is less incentive to fight over who gets to build the first superintelligence if everybody stands to benefit equally from any project’s success. The sponsors of a particular project might also benefit from credibly signaling their commitment to distributing the spoils universally, a certifiably altruistic project being likely to attract more supporters and fewer enemies.
38
The other prong of the prudential case for favoring a wide distribution of gains has to do with whether agents are risk-averse or have utility functions that are sublinear in resources. The central fact here is the enormousness of the potential resource pie. Assuming the observable universe is as uninhabited as it looks, it contains more than one vacant galaxy for each human being alive. Most people would much rather have certain access to one galaxy’s worth of resources than a lottery ticket offering a one-in-a-billion chance of owning a billion galaxies.
39
Given the astronomical size of humanity’s cosmic endowment, it seems that self-interest should generally favor deals that would guarantee each person a share, even if each share corresponded to a small fraction of the total. The important thing, when such an extravagant bonanza is in the offing, is to not be left out in the cold.
This argument from the enormousness of the resource pie presupposes that preferences are resource-satiable.
40
That supposition does not necessarily hold. For instance, several prominent ethical theories—including especially aggregative consequentialist theories—correspond to utility functions that are risk-neutral and linear in resources. A billion galaxies could be used to create a billion times more happy lives than a single galaxy. They are thus, to a utilitarian, worth a billion times as much.
41
Ordinary selfish human preference functions, however, appear to be relatively resource-satiable.
This last statement must be flanked by two important qualifications. The first is that many people care about rank. If multiple agents each wants to top the Forbes rich list, then no resource pie is large enough to give everybody full satisfaction.
