Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (70 page)
Read Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 Online
Authors: Judith A. Muschla,Gary Robert Muschla,Erin Muschla-Berry
Tags: #Education, #Teaching Methods & Materials, #Mathematics, #General

BOOK: Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5
9.62Mb size Format: txt, pdf, ePub
Working first individually, then in groups, students will brainstorm to generate a list of at least three examples of real-life situations that show fractions as the division of a numerator by a denominator. Based on the situations, they will create problems, draw models, and write equations that will be used to solve the problems.
Materials
Ruler; compass; unlined paper for each student.
Procedure
1.
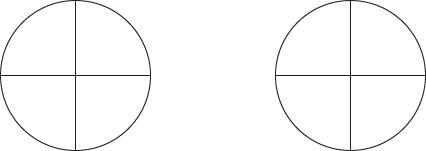
Present the following problem: Sam, Tyler, Sophie, and Jorge buy two large pizzas. If they share the pizzas equally, what fraction of a whole pizza does each person eat? Draw a model and write an equation to help you solve the problem.
2.
Provide a few minutes for your students to work on this problem individually. Then have them share their answers, equations, and models with a partner.
3.
Have volunteers show their work on the board and explain how they solved the problem.
4.
Explain that this problem could be modeled by the equationbecause four friends are sharing two pizzas equally. A possible model is shown below. The two circles, representing the pizzas, are split into 4 equal pieces each, showing that four people are splitting the pizza. Each person would receive
or
of a pizza.
5.
Explain that students will now work in their groups and create similar problems. First, they are to brainstorm a list of at least three real-life situations that show fractions as division of a numerator by a denominator. Suggest that they consider the example of the shared pizzas and generate some situations of their own, such as boxes of markers shared by four students or dividing a small birthday cake among six partygoers.
6.
After groups create their lists, ask each group to share its list. Make sure that the situations they developed are applicable to division.
7.
Instruct the groups to write three word problems, based on their lists.
8.
After each group has completed writing their word problems, instruct them to provide solutions using models and writing equations on a separate sheet of paper.
9.
Have each group trade their problems with another group. (They should not trade models and equations at this time.) Groups are to solve each other's problems, creating their own models and writing equations. When each group has solved the other's problems, have them trade the original models and equations to double-check their work.
Closure
Discuss students' work. Have volunteers share a problem and show their model and equation on the board. Ask students: How can models and equations help in finding the solution to a problem?
Number and Operations—Fractions: 5.NF.4
“Apply and extend previous understandings of multiplication and division to multiply and divide fractions.”
4. “Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
a.
“Interpret the productas
parts of a partition of
into
equal parts; equivalently, as the result of a sequence of operations
.
b.
“Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.”
Background
The standard algorithm for multiplying a fraction by a fraction is to find the product of the numerators and find the product of the denominators, and then write the product of the numerators over the product of the denominators. Simplify, if necessary. For example,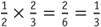 .
.
In the case of multiplying a whole number by a fraction, the whole number must first be written as an improper fraction. The process for multiplying a fraction by a fraction is then followed. For example,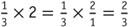 .
.
Other books
You Were My Crush: Till You Said You Love Me! by Durjoy Datta, Orvana Ghai
Taking the High Road by Morris Fenris
We the Living by Ayn Rand
Insolence by Lex Valentine
Airs and Graces by Roz Southey
Mad Hatter's Alice by Kelliea Ashley
Rodzina by Karen Cushman
It's My Life (Filming Rhiannon. Book 1) by TL Messruther
Hard to Handle by Diana Palmer
Dragonstar Destiny by David Bischoff, Thomas F. Monteleone