The Cosmic Landscape (32 page)

The discovery of String Theory, which in a sense is still ongoing, was full of twists of fate, reversals of fortune, and serendipity. My own involvement with it began sometime in 1968 or early 1969. I was beginning to tire of the problems of elementary particles, especially hadrons, which seemed to have little to offer in the way of deep, new principles. I found the S-matrix approach boring and was beginning to think about the relation between quantum mechanics and gravity. Putting the General Theory of Relativity together with the principles of quantum mechanics seemed far more exciting, even if all the experimental data were about hadrons. But just at that time, a friend from Israel visited me in New York. The friend, Hector Rubinstein, was extremely excited about Veneziano’s work. At first I was not very interested. Hadrons were exactly what I wanted to forget about. Mainly out of politeness I decided to hear Hector out.

Hector became so excited while explaining the Italian’s idea that I really couldn’t follow the details. As far as I could make out, Veneziano had worked out a formula for describing what happens when two hadrons collide. He finally wrote down Veneziano’s formula on the blackboard in my office. It immediately struck a chord. It was extremely simple, and features of the formula looked familiar to me. I recall asking Hector, “Does this formula represent some kind of simple quantum-mechanical system? It looks like it has something to do with harmonic oscillators.” Hector didn’t know of a physical picture that went with the formula, so I wrote it down on a sheet of paper to remember.

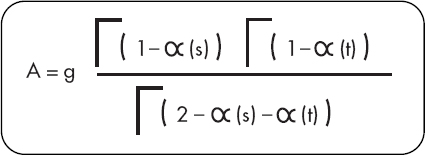
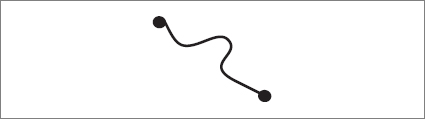
I was intrigued enough to postpone thinking about quantum gravity and give hadrons another chance. As it turned out I didn’t seriously think about gravity again for more than a decade. I pondered the formula above for several months before I began to see what it really represented.

The term
harmonic oscillator
is physics language for anything that can vibrate or swing back and forth with a periodic (repeating) motion. A child on a playground swing or a weight hanging at the end of a spring are familiar harmonic oscillators. Vibrations of a violin string or even the oscillations of the air when a sound wave passes through it are also good examples. If the vibrating system is small enough—the vibrations of atoms in a molecule are an example—then quantum mechanics becomes important, and energy can be added to the oscillator only in discrete steps. I had mentioned the harmonic oscillator to Hector because certain features of Veneziano’s formula reminded me of the mathematical properties of quantum-mechanical harmonic oscillators. I imagined a hadron as two weights connected by a spring, vibrating in periodic oscillation—the weights first approaching and then receding from each other. I was clearly playing with forbidden fruit, trying to picture the internal machinery inside elementary particles, and I knew it.

Being tantalizingly close to the answer but not quite being there is maddening. I tried all sorts of quantum-mechanically oscillating systems, attempting to match them with Veneziano’s formula. I was able to produce formulas that looked a lot like Veneziano’s from the simple weight and spring model, but they weren’t quite right. During that period I spent long hours by myself, working in the attic of my house. I hardly came out, and when I did I was irritable. I barked at my wife and ignored my kids. I couldn’t put the formula out of my mind, even long enough to eat dinner. But then for no good reason, one evening in the attic I suddenly had a “eureka moment.” I don’t know what provoked the thought. One minute I saw a spring, and the next I could visualize an elastic string, stretched between two quarks and vibrating in many different patterns of oscillation. I knew in an instant that replacing the mathematical spring with the continuous material of a vibrating string would do the trick. Actually, the word
string
is not what flashed into my mind. A
rubber band
is the way I thought of it: a rubber band cut open so that it became an elastic string with two ends. At each end I pictured a quark or, more precisely, a quark at one end and an antiquark at the other.

I quickly did a few calculations in my notebook to test the idea, but I already knew that it would work. The simplicity of it was stunning. Veneziano’s S-matrix formula precisely described two colliding “rubber bands.” I didn’t know why I hadn’t thought of it earlier.

Nothing is quite like the excitement of a new discovery. It doesn’t happen often, even for the greatest physicists. You say to yourself, “Here I am, the only one on the planet who knows this thing. Soon the rest of the world will know, but for the moment I am the
only one.
” I was young and unknown but with visions of glory.

But I wasn’t the
only one.
At just about the same time, a physicist in Chicago was doing the same calculations. Yoichiro Nambu was a good deal older than I and had long been one of the most eminent theoretical physicists in the world. Born in Japan, he came to the University of Chicago as a young physicist right after World War II. Nambu was a star who had the reputation of seeing things long in advance of anyone else. Later I was to find out that yet another physicist in Denmark, Holger Bech Nielsen, was thinking about very similar ideas. I won’t deny that I was disappointed when I found out that I wasn’t alone in thinking of the “rubber band theory,” but being in the same company as the great Nambu had its own satisfactions.

Today’s modern String Theory is all about the elusive unification of quantum mechanics and gravity, over which physicists banged their collective head for much of the twentieth century. That means that it is a theory of what the world is like at that fabulously tiny scale of the Planck length, 10
^–33
centimeters. As I have explained, it started out much more modestly as a theory of hadrons. We will see in the next chapter how it morphed into a much deeper fundamental theory, but let’s follow its earlier incarnation.

Hadrons are small objects, typically about 100,000 times smaller than an atom. This makes them 10
^–13
centimeters in diameter. It takes an enormous force to bind quarks at such small separation. Hadronic strings, the rubber bands of my imagination, although microscopically small, are prodigiously strong. If you could find a way to attach one end of a meson (one kind of hadron) to a car and the other end to a crane, you could easily lift the car. Hadronic strings are not particularly small on the scale of today’s experiments. Modern accelerators are probing nature at scales from a hundred to a thousand times smaller. Just for comparison let me get ahead of the story and tell you what the strength of a string is in the modern reincarnation. In order to hold particles together at the Planck distance, a string would have to be about 10
⁴⁰
times stronger than the hadronic strings; one of them could support a weight equal to the entire mass of our galaxy if we could somehow concentrate the galaxy at the surface of the earth.

All hadrons belong to one of three families: baryons, mesons, and glueballs. Nucleons, the ordinary protons and neutrons of nuclear physics, are the most familiar hadrons. They belong to the first family, called baryons.
²
All baryons are composed of three quarks. The quarks are connected to one another by means of three strings in the manner of a gaucho’s bola: three strings joined at the center, with three quarks at their ends. The only thing wrong with the bola picture is that the hadronic strings are elastic, much like ideal stretchable bungee cords. The ordinary proton and neutron are the lowest energy configurations of the bola, with the quarks at rest at the ends of very short, unstretched strings.

The quarks at the ends of the strings can be set into motion in a number of ways. The bola can be spun around its center, the centrifugal force stretching the strings and pushing the quarks out from the center. This spinning motion requires energy (remember E = mc
²
), and that makes spinning hadrons heavier. As noted earlier, the jargon for a particle with extra energy is that it is excited. The quarks can also be excited without rotating. One way is through oscillating motions, moving toward and away from the center, in and out, in and out. In addition the strings themselves can be bent into curved, vibrating patterns almost as if they were plucked with a guitar pick. All of these motions, or at least indirect evidence of them, are routinely seen in real experiments on nucleons. Baryons really do behave like elastic quantum bolas.

What does it mean that they are quantum bolas? Quantum mechanics implies that the energy (mass) of any vibrating system can be added only in indivisible, discrete steps. In the earliest days of experimental hadron physics, physicists didn’t realize that the discretely different quantum states of the vibrating system were really the same object. They gave each energy level a different name and considered them all to be different particles. The proton and the neutron were the baryons with the least energy. The more massive ones had odd names that would mean absolutely nothing to most young physicists today. These particles are nothing more than rotating or vibrating excited states of the proton and neutron. When this was realized, of course, it brought a lot of order and unity to what had been a very messy zoo of particles.

Next come the mesons, the particles that I studied in my attic in 1969. They are simpler than baryons. Each meson is made of a single string with a quark at one end and an antiquark at the other. Mesons, like baryons, can rotate and vibrate in discrete quantum steps. The calculation that I did in the attic represented a fundamental process of interaction between two meson strings.

When two mesons collide they can do a number of things. Because quantum mechanics is a theory of probabilities, it is impossible to predict with certainty how the history of the collision will unfold. One possibility, in fact the most likely one, is that the two mesons will go right past each other, even if it means that the strings pass through each other. But a second, more interesting, possibility is that they can fuse, joining together, to form a single, longer string.

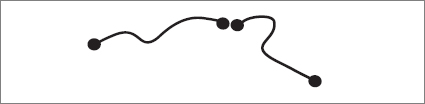
Imagine each string to be a group of dancers holding hands to form a line. At each end the dancers have one hand free (a quark or antiquark); all the others have both hands occupied. Picture the two lines racing toward each other. The only way they are allowed to interact is by a dancer at the end of one line clasping a free hand of the other group. Once they are joined they form a single chain. In this configuration they swing around one another in a complicated dance until somewhere along the chain a dancer releases his neighbor’s hand. Then the chain splits into two independent chains, and off they go, separating in some new direction. More precisely but less colorfully, the quark from the end of one string comes together with the antiquark of the other string. They collide and annihilate, as always, when a particle and an antiparticle come together. What they leave over is a single, longer string with a single quark and a single antiquark.