The Cosmic Landscape (37 page)

The winding number is a property of a particle that we could not understand if our microscope was not strong enough to resolve the tiny distance around the compact direction. So you see, the extra dimensions needed by String Theory are a blessing, not a curse: they are essential for understanding the complex properties of elementary particles.
A two-dimensional cylinder is easy to visualize, but a nine-dimensional space with six dimensions wrapped up into some kind of six-dimensional tiny space is beyond anyone’s powers of visualization. But making pictures in your head or on paper is not the only way to understand the mind-boggling six-dimensional geometry of String Theory. Geometry can often be reduced to algebra just the way you learned in high school when you used an equation to represent a straight line or a circle. Still, even the most powerful methods of mathematics are barely enough to scratch the surface of six-dimensional geometry.
For example, the number of possible ways String Theory allows of rolling up six dimensions runs into the millions. I won’t try to describe them other than to give you the special mathematical name for these spaces; they are called
Calabi Yau spaces,
after the two mathematicians who first studied them. I don’t know why mathematicians were interested in these spaces, but they came in handy for string theorists. Fortunately for us the only thing we have to know is that they are extremely complicated, with hundreds of “donut holes” and other features.
Back to the two-dimensional cylinder. The distance around the cylinder is called the
compactification scale.
For a cardboard cylinder it might be a few inches, but for String Theory it should most likely be a few Planck lengths. You might think that this scale is so small that it doesn’t matter for anything we care about, but that’s not so. Although we can’t actually see such small scales, they nonetheless have their effect on ordinary physics. The compactification scale in Kaluza’s theory fixes the magnitude of the electric charge of a particle like the electron. It also fixes the masses of many of the particles. In other words the scale of compactification determines various constants that appear in the ordinary Laws of Physics. Vary the size of the cylinder, and the Laws of Physics change. Vary the values of scalar fields as in chapter 1, and the Laws of Physics change. Is there a connection? Absolutely! And we will return to it.
To specify the cylinder you need to specify only one parameter, the scale of compactification, but other shapes require more. For example, a torus is determined by three parameters. See if you can visualize them. First there is the overall size of the torus. Keeping the shape fixed, the torus can be magnified or shrunk. In addition, the torus can be “thin” like a narrow ring or “fat” like an overstuffed bagel. The parameter that determines the fatness is a ratio: the ratio of the size of the hole to the overall size. For the thin ring, the overall size and the size of the hole are about the same, so the ratio is near one. For the fat torus the hole is much smaller than the overall size, and the ratio is correspondingly small. There is one more quantity, which is harder to picture. Imagine taking a knife and cutting the ring, not in half but just so that it can be opened up to a section of a cylinder. Now twist one end of the cylinder, keeping the other end fixed. Finally, reconnect the ends of the cylinder so that it becomes a ring but with a twist. The angle of the twist is another variable. If you can’t picture it, that’s okay. You won’t need to.
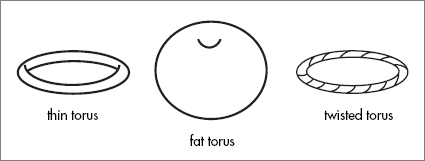
Mathematicians call these parameters that determine the size and shape of the torus moduli (plural of
modulus
). A torus has three moduli. The cylinder, or more accurately, the circular cross section of the cylinder, has only one modulus. But a typical Calabi Yau space has hundreds. Perhaps you can see where this is going, but if not, I will spell it out. It is leading us to a Landscape—and an incredibly complicated one at that.
One very important issue is whether the size and shape of the compact component of the space can vary from one point to another. Visualize a clumsily constructed cylinder. Suppose that as you move along the length of the cylinder, the circumference of the cross section varies: here the cylinder is narrow, there it’s wider.
Keep in mind that even if the cylinder is extremely thin, far too thin to detect its compact dimension, the size of that dimension determines various coupling constants and masses. Evidently we have made a world where the Laws of Physics can vary from point to point. What does an ordinary physicist who cannot see the small dimension make out of all this? She says: “Conditions are varying from point to point. It seems that some kind of scalar field controls the value of the electric charge and mass of particles, and it can vary from point to point.” In other words, the moduli form some kind of Landscape—a Landscape of hundreds of dimensions.
A Calabi Yau space is vastly more complicated than the circular cross section of the cylinder, but the principle is the same: the size and shape of the compact space can vary with position just as if there were hundreds of scalar fields controlling the Laws of Physics! Now we begin to see why the Landscape of String Theory is so complicated.
The real underlying principles of String Theory are largely shrouded in mystery. Almost everything we know about the theory involves a very special portion of the Landscape where the mathematics was amazingly simplified by a property that was mentioned in chapter 2 called supersymmetry. The supersymmetric regions of the Landscape form a perfectly flat plain at exactly zero altitude, with properties so symmetric that many things can be deduced without having complete mastery of the entire Landscape. If one were looking for simplicity and elegance, the flat plain of supersymmetric String Theory, a.k.a. superString Theory, is the place to look. In fact until a couple of years ago it was the only place string theorists looked. But some theoretical physicists are finally waking up and trying to wean themselves off the elegant simplifications of the superworld. The reason is simple: the real world is not supersymmetric.
The world of experience that includes the Standard Model and a small cosmological constant is not located on this plain of zero altitude. It is somewhere in the rough, textured regions of the Landscape with hills, valleys, high plateaus, and steep descents. But there is at least some reason to think that our valley is close to the supersymmetric part of the Landscape and that there may be remnants of the mathematical supermiracles that would help us understand features of the empirical world. One example that we will encounter in this section involves the mass of the Higgs boson. In a real sense the discoveries that made this book possible are all about the initial timid explorations away from the safety of the supersymmetric plain.
Supersymmetry is all about the distinctions and similarities of bosons and fermions. As with so much else in modern physics, the principles trace back to Einstein. The year 2005 marks the one hundredth anniversary of the
anno mirabilis
—the “miracle year”—of modern physics. Einstein set two revolutions in motion that year and completed a third.
3
It was of course the year of the Special Theory of Relativity. But what many people don’t know is that 1905 was much more than the “relativity year.” It also marked the birth of the photon, the start of modern quantum mechanics.
Einstein received only one Nobel Prize in physics, although I think it’s fair to say that almost every prize given after 1905 was in one way or another a tribute to his discoveries. The prize was ultimately awarded not for relativity but for the photoelectric effect. This, the most radical of Einstein’s contributions, is where the idea that light is composed of discrete quanta of energy was first argued. Physics was ready for the Special Theory of Relativity. In fact it was overdue. But the photon theory of light was a bolt from the blue. As noted previously, Einstein argued that a beam of light, usually thought of as a pure wave phenomenon, had a discrete, or grainy, structure. If the light had a definite color (wavelength), then the photons would all be marching in lock step, each photon identical to every other photon. Particles that can all be in the same quantum state like photons are called bosons, after the Indian physicist Satyendra Nath Bose.
Almost twenty years later, building on Einstein’s work, Louis de Broglie closed the cycle by showing that electrons, the quintessential particles, have a wavelike side to them. Like other waves, electrons can reflect, refract, diffract, and interfere. But there is a fundamental difference between electrons and photons: unlike photons, no two electrons can ever occupy the same quantum state. The Pauli exclusion principle ensures that each electron in an atom must exist in its own quantum state and that no other electron can ever shoulder its way into an already occupied state. Even outside an atom, two otherwise identical electrons cannot have the same position or the same momentum. Particles of this kind are called fermions, after the Italian physicist Enrico Fermi, although they should be called paulions. Of all the particles of the Standard Model, about half are fermions (electrons, neutrinos, and quarks) and half are bosons (photons, Z- and W-bosons, gluons, and Higgs bosons).
Fermions and bosons play very different roles in the grand design. Ordinarily we think of matter as made up of atoms, and that means electrons and nuclei. To review, the nuclei at one level are bunches of protons and neutrons stuck together by means of the nuclear force, but at a deeper level, the protons and neutrons are made of even smaller building blocks—quarks. All of these particles—electrons, protons, neutrons, and quarks—are fermions. Matter is made of fermions. But without bosons the atoms and nuclei as well as the protons and neutrons would just fall apart. It’s the bosons, especially photons and gluons, hopping back and forth between fermions that create the attraction holding everything together. Although both fermions and bosons are critically important to making the world what it is, they were always thought of as very different kinds of creatures.
But sometime in the early 1970s, as a consequence of discoveries by string theorists, physicists began to play around with a new mathematical idea, the idea that fermions and bosons are not really so different. The idea is that all particles come in precisely matched pairs, identical twins that are the same in every way except that one is a fermion and one is a boson. This was a wild hypothesis. If true in the real world, it would mean that physicists had completely missed half the particles of nature, had failed to discover them in their labs. For example, this new principle would require that there is a particle exactly like the electron—same mass and charge—except that it would be a boson. How could we have failed to detect it in particle physics laboratories like SLAC and CERN? Supersymmetry implies that a fermion twin for the photon, massless and with no electric charge, would have to exist. Similarly, boson partners for electrons and quarks would be required. A complete world of “opposites” was mysteriously missing if this new idea were right. In fact the whole exercise was only a mathematical game, a pure theoretical exploration of a new kind of symmetry that a world—some world not our own—might possess.
The identical twins don’t exist. Physicists didn’t blunder and miss a whole parallel world. Why, then, is there interest in such idle mathematical speculation—interest that has only intensified over the last thirty years? Physicists are always interested in possible mathematical symmetries, even if the only question is why they aren’t part of nature. But also both the real world and the physicist’s description of it are full of symmetry. Symmetry is one of the most far-reaching and powerful weapons in the arsenal of theoretical physics. It permeates every branch of modern physics, particularly those that have to do with quantum mechanics. In many cases all we really know about a physical system is its symmetries, but so powerful are these symmetries that they sometimes tell us almost everything we want to know. Symmetries are often at the core of what physicists find esthetically pleasing about their theories. But what are they?
