The Dancing Wu Li Masters (20 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

There are many examples of proper time and relative time. Suppose that we are in a space station observing an astronaut who is traveling at a speed of 161,000 miles per second relative to us. As we watch him, we notice a certain sluggishness in his movements, as though he were moving in slow motion. We also notice that everything in his spaceship also seems to function in slow motion. His rolled cigarette, for example, lasts twice as long as one of ours.
Of course, part of his sluggishness is due to the fact that he is fast increasing the distance between us, and with each passing moment, it takes the light from his spaceship longer to reach us. Nonetheless, after making allowances for the travel time of the light involved, we find that the astronaut still is moving more slowly than usual.
However, to the astronaut, it is we who are zipping past him at 161,000 miles per second, and after he makes all the necessary allowances, he finds that it is we who are sluggish. Our cigarette lasts twice as long as his.
This situation could be the ultimate illustration of how the grass is always greener on the other side. Each man’s cigarette lasts twice as long as the other’s. (Unfortunately, so does each man’s trip to the dentist.)
The time that we ourselves experience and measure is our proper time. Our cigarette lasts the normal length of time. The time that we measure for the astronaut is the relative time. His cigarette appears to last twice as long as ours because his time passes twice as slowly. The situation is similar regarding proper lengths and relative lengths. From our point of view, the astronaut’s cigarette, provided that it is pointing in the direction that his spaceship is moving, is shorter than our own cigarette.
The other side of the coin is that the astronaut sees himself as stationary and his cigarettes as normal. He also sees us as traveling at 161,000 miles per second relative to him, and our cigarettes as shorter than his and slower burning.
Einstein’s theory has been substantiated in many ways. All of them verify it with awesome accuracy.
The most common verifications of time dilation come from high-energy particle physics. A very light elementary particle, called a muon (pronounced moo’on), is created at the top of the earth’s atmosphere by the collision of protons (one form of “cosmic radiation”) and air molecules. We know from experiments in which muons are created in accelerators that they live a very short time. By no means do they live long enough to reach the earth from the upper atmosphere. Long before the time it takes to traverse this distance, they should decay spontaneously into other types of particles. Yet this does not happen because we detect them in abundance here at the earth’s surface.
Why do the muons created by cosmic radiation live longer, in fact,
seven times longer
than those muons created in the laboratory? The answer is that the muons produced by collisions of cosmic radiation and air molecules travel much faster than any muons that we can create experimentally. Their velocity is approximately 99 percent of the speed of light. At that speed, time dilation is quite noticeable. They do not live longer than usual from
their
point of view, but from our point of view they live seven times longer than they would at slower velocities.
This is true not only of muons, but of almost all subatomic particles, and there are many of them. For example, pions (pie’ons), another type of subatomic particle, which move at 80 percent of the speed of light, live, on the average, 1.67 times as long as slow pions. The special theory of relativity tells us that the intrinsic lifetime of these high-speed particles does not increase, but that their relative rate of time flow slows down. The special theory of relativity also made the calculation of these phenomena possible long before we had the technical capability to create them.
In 1972, four of the most accurate atomic clocks available were put aboard an aircraft and flown around the world. At the end of the trip, they were found to be slightly behind their stationary, earthbound counterparts with which they were synchronized before the
flight.
*
The next time that you fly, remember that, even if minutely, your watch is running slower, your body had more mass, and, if you stand facing the cockpit, you are thinner.
According to the special theory of relativity, a moving object appears to contract in the direction of motion as its velocity increases. James Terrell, a physicist, has demonstrated mathematically that this phenomenon is something like a visual illusion, and, in fact, is analogous to a projection of the real world onto the wall of Plato’s cave.
6
Plato’s famous parable of the cave describes a group of people who are chained inside a cave in such a way that they can see only the shadows on the wall of the cave. These shadows are the only world that these people know. One day one of these people escapes into the world outside the cave. At first he is blinded by the sunlight, but when he recovers, he realizes that
this
is the real world, and what he previously considered to be the real world was, in fact, only the projection of the real world onto the wall of the cave. (Unfortunately, when he returned to the people who still were chained inside the cave, they thought he was mad.)
Figure A, on the next page, depicts a view looking down on the top of our head and the top of a sphere. The lines connect our eyes with points on either side of the sphere. If we are far enough away from the sphere, the distance between these points is almost equal to the diameter of the sphere. Figure A is drawn as if the artist were looking down on the top of our head, our eyes, and the sphere.
The first step in Terrell’s explanation is to draw lines downward (back into the page) from each of the two points on the sphere to a screen directly below the sphere. Figure B is a side view showing the two points, the lines that we have drawn downward, and the screen. (If you hold this book directly in front of you, your eyes are in the same position relative to the dotted lines as the eyes drawn in Figure A.)
To understand Terrell’s explanation, suppose that the sphere is
moving
very fast
relative to the speed of light from right to left. If the sphere moves fast enough, some very interesting things happen. For example, before the light from the point on the far left edge of the sphere can reach us, the ball moves in front of it, blocking it from our vision! The reverse happens on the far right. The ball moves out from between us and the light signals originating from points that used to be on the “back” side of the ball. These signals now are visible to us, while the signals coming from the point that used to be on the leading edge of the ball now are blocked by the ball itself as it moves to the left. The effect of this is an illusion of sorts. What we see is the same thing that we would see if someone had
rotated
the ball around its axis!
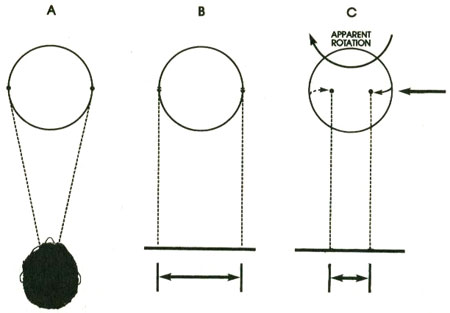
Look what happened to the distance between the two points as projected on the screen. It is considerably less than when we started. The equations in the special theory of relativity (the Lorentz transformations) which show a contraction due to motion describe these
projections
. (Is this beginning to sound like Plato’s cave?)
The fact that the ball, by moving fast enough, gets in the way of some of its own light signals and out of the way of others causes the
ball to appear to rotate. This causes the
projected
distance between any two points on it which are aligned with the direction of motion to decrease, just as if someone really had rotated the ball. The faster the ball moves, the more it appears to “rotate,” and the closer together come the points projected on the screen. It is the projection that contracts. Instead of “screen” substitute “view of the ball from our frame of reference” and we have the Terrell explanation of relativistic contraction.
As yet, no analogous explanations have been found for the time dilation that accompanies moving clocks or the increase of mass that accompanies moving objects, but the effort, relatively speaking, is young.
The special theory of relativity shows that the mass of a moving object increases as the velocity of the object increases. Newton would not have hesitated to call this nonsense, but then Newton’s experience was limited to velocities that are quite slow compared to the speed of light.
Classic physics tells us that a specific amount of force is required to increase the velocity of a moving object by a given amount, for example, one foot per second. Once we know what that amount of force is, whenever we want to increase the velocity of that particular object by one foot per second, all we need do is apply that amount of force to it. If the object has a velocity of 100 feet per second, that specific amount of force will increase its velocity to 101 feet per second. According to Newton’s physics, the same amount of force that increases the velocity of an object from 100 feet per second to 101 feet per second also will increase the velocity of the same object from 8,000 feet per second to 8,001 feet per second.
The problem is that Newtonian physics is wrong. It takes much more force to increase by one foot per second the velocity of an object moving at 8,000 feet per second than it takes to increase by one foot per second the velocity of the same object moving at 100 feet per second.
That is because a faster-moving object has more kinetic energy (energy of motion). This additional energy makes it behave exactly as if it had more mass. A given amount of force applied for a given amount of time will accelerate a force applied for the same amount of time to an entire train. Of course, this is because an entire train has more mass than a single car.
When particles travel at velocities that are fast relative to the speed of light, their high kinetic energy makes them behave as though they have more mass than they have at lower velocities. In fact, the special theory of relativity shows that the effective mass of a moving object
does
increase with velocity.
Since most subatomic particles travel at different velocities, each one of them can have many different relative masses. Therefore, physicists have calculated the “rest mass” of each particle. The rest mass of a subatomic particle is its mass when it is not moving. Subatomic particles are never really at rest, but these calculations provide a uniform method of comparing their masses. This is necessary since, as the velocity of a particle approaches the speed of light, its relative mass depends upon how fast it is moving.
Einstein’s discovery that moving clocks change their rhythm led to some spectacular revisions in the way that we see the world. It showed that there is no “universal” time that permeates the universe. There are only proper times associated with various observers. The proper time of each observer is different, unless two of them happen to be at rest relative to each other. If the universe has a heart beat, its rate depends upon the hearer.
The special theory of relativity shows that two events which happen at the same time in one frame of reference may occur at different times when seen from another frame of reference. To illustrate this point, Einstein used one of his famous thought experiments.
A thought experiment is a mental exercise. It has the advantage of requiring no apparatus other than the mind, which frees it from the practical limitations of laboratory experiments. Most physicists accept
the use of thought experiments as a valid theoretical tool, provided they are satisfied that if the experiment could be performed, the results of the actual experiment would be the same as those of the thought experiment.
Suppose that we are in a moving room. The room is moving with a uniform velocity. Exactly in the center of the room is a light bulb which flashes periodically. The room is made of glass so that an outside observer can see what happens inside.
At the precise moment that we pass an outside observer, the light flashes. The question is, is there any difference between what we see inside the moving room and what the outsider observer sees? According to the special theory of relativity, the answer is an extraordinary, concept-shattering
Yes
. There is a big difference.
Inside the room, we see the bulb flash and we see the light spread out in all directions at the same speed. Since the walls of the room are equidistant from the bulb, we see the light strike the forward wall and rearward wall of the room simultaneously.
The outside observer also sees the flash, and he also sees the light propagate in all directions at the same speed. However, in addition, he sees that the room is moving. From his point of view the forward wall tries to escape the approaching light while the rearward wall rushes to meet it. Therefore, to the outside observer, the light reaches the rearward wall before it reaches the forward wall. If the speed of the room is small compared to the speed of light, the light reaches the rearward wall only slightly ahead of the forward wall. Nonetheless, the light reaches the rearward and forward walls in a one-two order, and not at the same time.
Although both of us observed the same two events, the light striking the forward wall and the light striking the rearward wall, we each have different stories to tell. To us, inside the room, the two events were simultaneous. To the outside observer, one event came first and the other event came later.
