The Dancing Wu Li Masters (50 page)

†
The Theory of Measurement presented here is essentially from John von Neumann’s 1932 discussion.

*
The wave function is the physicist’s description of reality. At issue is the interpretation of the wave function and whether it is the best possible description (or simply the only one that fits the language used by physicists).

*
The wave function, since it is a tool for our understanding of nature, is something in our thoughts. It represents certain
specifications
of certain physical systems. Specifications are objective in the sense that scientists and technicians can agree on them. However, specifications do not exist apart from thought. Also, any given physical system satisfies many sets of specifications, and many physical systems can satisfy one set of specifications. All of these characteristics are idea-like and, to that extent, that which is represented by the wave function is idea-like, even though it is objective.
      However, these specifications are transcribed into wave functions that develop according to a determined law (the Schrödinger wave equation). This is a matter-like aspect. The thing that develops describes only probabilities. Probabilities can be thought to describe either things that exist apart from thought, or things that exist only within thought. Thus that which the wave function represents has both idea-like and matter-like characteristics.

*
“How is one to apply the conventional formulation of quantum mechanics to the space-time geometry itself? The issue becomes especially acute in the case of a closed universe. There is no place to stand outside the system to observe it.”—Hugh Everett III (
Reviews of Modern Physics
, 29, 3, 1957, 455).

*
In practice, it is not clear that a macroscopic object such as a cat actually can be represented by a wave function due to the dominating influence of thermodynamically irreversible processes. Even so, Schrödinger’s cat long has illustrated to physics students the psychedelic aspects of quantum mechanics.

*
The dark-adapted eye can detect single photons. All of the other subatomic particles must be detected indirectly.

*
Individual events are always particle-like; wave behavior is detected as a statistical pattern, i.e., interference. However, in the words of Paul Dirac (another founder of quantum mechanics) even a single subatomic particle “interferes with itself.” How a single subatomic particle, like an electron, for example, can “interfere with itself” is the basic quantum paradox.

*
Planck’s equation: E = h
v
. Einstein’s equation: E = mc
²
. De Broglie’s equation: λ = h/mv.

^*
As you hold this photograph in front of you, the beam of electrons (the “transmitted beam”) is coming directly toward you out of the large white spot in the center. Also located in the white spot is the diffracting material (in this case, the electron beam is being diffracted by small grains of gold, i.e., the beam is being directed through a thin polycrystalline gold foil). The rings on the photograph mark the places where the diffracted electron beams struck the film which was placed on the opposite side of the gold foil from the electron source. The white spot in the center of the photograph was caused by undiffracted electrons in the transmitted beam passing through the gold foil and striking the film directly.

*
Accurately speaking, Schrödinger’s theory does not explain The Jump, either. In fact, Schrödinger did not like the idea of a “jump.”

*
These photographs are of mechanical simulations of probability density distributions of different electron states in the hydrogen atom. In other words, they represent where we are most likely to find the point-like electron when we look for it if the atom is in this or that particular state (there are more states than those shown). Initially, Schrödinger pictured electrons as being tenuous clouds actually assuming these patterns.

†
A “quantum jump” can be thought of as a transition from one of these pictures to another
without anything in between
.

*
Schrödinger’s early interpretation that electrons literally were standing waves did not stand up to detailed examination and he had to renounce it. Soon, however, the concept of probability based upon a wave function representing an observed system (and developing according to the Schrödinger wave equation) became a fundamental tool in atomic research and Schrödinger’s famous equation became an integral part of quantum theory. Since the Schrödinger wave equation is nonrelativistic, however, it does not work at high energies. Therefore, high-energy particle physicists usually use the S Matrix to calculate transition probabilities. (S Matrix theory is discussed in a later chapter.)

†
Until the propagating system interacts with a measuring device. That causes an abrupt, unpredictable transition to another state (a quantum jump).

*
If the state is prepared in state ψ(t), the probability that it will be observed to be in state φ(t) is | <Ψ(t)|φ(t)> |
²
. If it is prepared in state Ψ(t) then the probability that it will be observed in region δ at time t is δ∫
_d
³
× Ψ*(x, t) × Ψ(x, t).

*
The Schrödinger wave equation works at lower energies, however, since it is nonrelativistic, it does not work for high energies. Therefore, most particle physicists use the S Matrix together, perhaps, with local relativistic quantum fields to understand quarks and particles.

*
Strictly speaking, Newton’s laws do not disappear totally in the subatomic realm: they remain valid as operator equations. Also, in some experiments involving subatomic particles Newton’s laws may be taken as good approximations in the description of what is happening.

*
Einstein’s point of departure for the special theory of relativity came from the conflict of classical relativity and Maxwell’s prediction of a light speed, “c.” An often-told story tells how Einstein tried to imagine what it would be like to travel as fast as a light wave. He saw, for example, that the hands on a clock would appear to stand still, since no other light waves from the clock would be able to catch up with him until he slowed down.

*
Although we do not experience it directly, the orbital motion of the earth is accelerating.

*
The fixed stars provide such a reference frame as far as defining non-rotation.

*
In a vacuum. The speed of light changes in matter depending upon the index of refraction of the matter: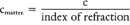

*
The reverse situation (the source moves and the observer remains stationary) is explainable in terms of prerelativistic physics. In fact, if light is assumed to be a wave phenomenon governed by a wave equation, it is
expected
that its measured velocity will be independent of the velocity of its source. The velocity of the sound waves reaching us from a jet plane, for example, does not depend upon the velocity of the aircraft. They propagate through a medium (the atmosphere) at a given velocity, from their point of origin, regardless of the motion of the plane (the
frequency
of the sound shifts as the source moves, e.g., the Doppler effect). Prerelativity theory assumes a medium (like the atmosphere, for sound waves, or the ether, for light waves) through which the waves propagate. The paradox is that the measured velocity of light has been found (the Michelson-Morley experiment) to be independent of the motion of the observer. In other words, assuming a light wave propagating through a medium, how can we move through the same medium toward the approaching wave without increasing its measured velocity?

*
Quantum field theory resurrects a new kind of ether, e.g., particles are excited states of the featureless ground state of the field (the vacuum state). The vacuum state is so featureless and has such high symmetry that we cannot assign a velocity to it experimentally.

*
It is said that the reasoning process by which Einstein discovered the special theory of relativity did not include the results of the Michelson-Morley experiment. However, the results of this well-publicized experiment were “in the air” for eighteen years prior to Einstein’s paper on special relativity (1905) and they led to the Lorentz transformations which became central to the mathematical formalism of special relativity.

*
In a vacuum. The speed of light changes in matter depending upon the index of refraction of the matter.

*
The clocks were flown around the world each way (east and west). Both general relativistic and special relativistic effects were noted. (J. C. Hafele and R. E. Keating,
Science
, vol. 177, 1972, pp. 168ff.)

*
This is only true for events that are space-like separated. For time-like separated events the relation earlier-later is preserved for all observers. Time-like separated events can never appear simultaneous in any frame of reference moving with a velocity less than c. (Space-like separation is explained later.)

*
The Pythagorean theorem is c
²
= a
²
+ b
²
. The equation for the space-time interval in the special theory of relativity is s
²
= t
²
- x
²
. The Pythagorean theorem describes properties in Euclidean space. The equation for the space-time interval describes properties in Minkowski’s flat space-time (Euclidean and non-Euclidean space are discussed in the next chapter). There are other differences as well, but the fundamental relationship between space, time, and the space-time interval is very similar to the relationship expressed in the Pythagorean theorem between the three sides of a right triangle.

*
Thanks to Guy Murchie who drew the original version of this drawing in his fine book,
Music of the Spheres
, New York, Dover, 1961.

*
As its hydrogen becomes exhausted, a star begins to fuse the helium at its core. Helium fusion is hotter than hydrogen fusion and produces heavier elements, such as neon, oxygen, and carbon, which, in turn, becomes the solar fuel as its helium becomes exhausted.

*
The view presented here is not that geometry comes from the mind. There are many possible geometries (as Riemann and Lobachevsky showed before Einstein), but the actual geometry that we have is determined by the physics. For example, Euclid considered geometry to be closely related to experience (he defined congruence by moving triangles about in space) and he considered his parallel axiom to be not self-evident, i.e., not a product purely of the mind.
      The view presented here is that idealizations abstracted from experience (like Euclidean geometry) form a rigid structure of such durability that, when subsequent sensory experience contradicts it, we question the validity of the sensory data rather than the validity of the idealized abstractions. Once such a set of idealized abstractions is erected (verified) in the mind, we thereafter superimpose it upon all subsequent actual and projected sense data (i.e., upon the entire universe as we picture it according to this set of abstractions), whether it fits or not.

*
The special theory deals with the unaccelerated (uniform) motion of
co-ordinate systems
. The special theory can be used to describe the accelerated (non-uniform) motion of
objects
as long as the co-ordinate system from which the object is being observed is itself in uniform motion.

*
Some physicists think that general relativity will be useful on the microscale of high-energy physics (where the effects of gravity usually are ignored), e.g., strong fluctuations of the gravitational field have been detected at very short distances (10
^-14
cm).

*
Eddington expressed this concept most concisely: “
A field of force represents the discrepancy between the natural geometry of a co-ordinate system and the abstract geometry arbitrarily ascribed to it
.” (Arthur Eddington,
The Mathematical Theory of Relativity
, Cambridge, England, Cambridge University Press, 1923, pp. 37–38. Italics in the original.)

*
This distance, of course, is “invariant,” i.e., the same for all co-ordinate systems. The invariance is the absolute objective aspect of Einstein’s theory that complements the subjective arbitrary choice of co-ordinate system.

†
The space-time continuum is not only curved, it also has topological properties, i.e., it can be connected in crazy ways, e.g., like a donut
. It also can twist (i.e., torsion).