The Numbers Behind NUMB3RS (11 page)
Read The Numbers Behind NUMB3RS Online
Authors: Keith Devlin

The key technique is called segmentationâsplitting up the image into distinct regions that correspond to distinct objects or parts of objects in the original scene. (One particular instance of segmentation is distinguishing objects from the background.) Once the image has been segmented, missing information within any given segment can be re-introduced by an appropriate averaging technique. There are several different methods for segmenting an image, all of them very technical, but we can describe the general idea.
Since digital images are displayed as rectangular arrays of pixels, with each pixel having a unique pair of x,y coordinates, any smooth edge or line in the image may be viewed as a curve, defined by an algebraic in the classical sense of geometry. For example, for a straight line, the pixels would satisfy an equation of the form
Â
y = mx + c
Â
Thus, one way to identify any straight-line edges in an image would be to look for collections of pixels of the same color that satisfy such an equation, where the pixels to one side of the line have the same color but the pixels on the other side do not. Likewise, edges that are curved could be captured by more complicated equations such as polynomials. Of course, with a digitized image, as with a scene in the real world, the agreement with an equation would not be exact, and so you'd have to allow for a reasonable amount of approximation in satisfying the equation. Once you do that, however, then you can take advantage of a mathematical fact that any smooth edge (i.e., one that has no breaks of sharp corners) can be approximated to whatever degree of accuracy you desire by a collection of (different) polynomials, with one polynomial approximating one part of the edge, another polynomial approximating the next part of the edge, and so on. This process will also be able to handle edges having sharp corners; at a corner, one polynomial takes over from the previous one.
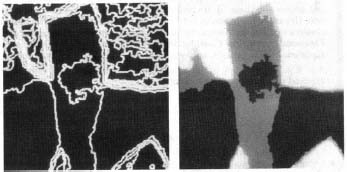
Figure 6. The result of the segmentation algorithm run on the photograph of the left arm of the Reginald Denny assailant, showing a mark entirely consistent with the rose tattoo on Damian Williams' left arm.
This simple idea shows how the problem of verifying that a given edge
is indeed an edge
can be reduced to a problem about finding equations. Unfortunately, being able to find an equation whose curve approximates a segment of a
given
edge does not help you identify that edge in the first place. For humans, recognizing an edge is generally not a problem. We (and other creatures) have sophisticated cognitive abilities to recognize visual patterns. Computers, however, do not. What they do excel at is manipulating numbers and equations. Thus, the most promising approach to edge detection would seem to be to manipulate equations in some systematic way until you find one that approximates the given edge segmentâthat is, such that the coordinates of the points on the edge segment approximately satisfy the equation. figure 6 shows the result of the Cognitech segmentation algorithm applied to the crucial left-arm portion of the aerial photograph in the Reginald Denny beating case.
This, in essence, is how segmentation works, but the successful implementation requires the use of mathematics well beyond the scope of this book. For the benefit of readers with some familiarity with college-level mathematics, the following section provides a brief account of the method; readers without the requisite background should simply skip the section.
IMAGE ENHANCEMENT: THE INSIDE SCOOP
Image enhancement is easier with black-and-white (more precisely, gray-scale) images than full color, so we'll look just at that special case. Given this restriction, a digital image is simply a function F from a given rectangular space (say, a grid 1000 Ã 650) into the real unit interval [0,1] (i.e., the real numbers between 0 and 1 inclusive). If F(x,y) = 0, then pixel (x,y) is colored white, if F(x,y) = 1, the pixel is colored black, and for all other cases F(x,y) denotes a shade of gray between white and black; the greater the value of F(x,y), the closer the pixel (x,y) is to being black. In practice, a digital image assigns gray-scale values to only a finite number of pixelsâthe image consists of a grid of pixels. To do the mathematics, however, we assume that the function F(x,y) is defined on the entire rectangle, that is to say, F(x,y) gives a value for any real numbers x, y within the stipulated rectangle. This allows us to use the extensive and powerful machinery of two-dimensional calculus (i.e., calculus of real-valued functions of two real variables).
The method used by the Cognitech team was based on an idea Rudin had when working as a graduate student intern at Bell Laboratories in the early 1980s, and developed further in his doctoral dissertation submitted at Caltech in 1987. By asking himself fundamental questions about visionâ“Why do we see a single point on a sheet of paper?” or “How do we see edges?” or “Why is a checker board pattern with lots of squares so annoying to the eye?” or “Why do we have difficulty understanding blurry images?”âand linking those questions to the corresponding mathematical function F(x,y), he realized the significance of what are called the singularities in the function. These are the places where the derivative (in the sense of calculus) becomes infinite. This led him to focus his attention on a particular way to measure how close a particular function is to a given imageâthe so-called total variation norm. The details are highly technical, but not required here. The upshot was that, together with colleagues at Cognitech, Rudin developed computational techniques to restore images using what is now called the total variation method.
*
MATH IN COURT
In addition to its obvious uses in military intelligence, the methods Cognitech developed found early applications in the enhancement of satellite images for nonmilitary purposes such as oil spill detection, and in the processing of images obtained by MRIs to identify tissue abnormalities such as tumors or obstructed arteries. By the time of the Damian Williams trial, the company was well established and ideally placed to make its groundbreaking contribution.
In addition to enhancing the key image that identified Damian Williams as the man who threw a concrete slab at Denny's head, Rudin and his colleagues also used their mathematical techniques to obtain other photograph-quality still images from video footage of the events, thereby identifying Williams as the perpetrator of assaults on several other victims as he moved from place to place that day.
Anyone who has viewed a freeze-frame of a video recording on a VCR will have observed that the quality of the image is extremely low. Video systems designed for home or even for news reporting take advantage of the way the human visual system works, to reduce the camera's storage requirements. Roughly speaking, each frame records just half the information captured by the lens, with the next frame recording (the updated version of) the missing half. Our visual system automatically merges the two successive images to create a realistic-looking image as it perceives the entire sequence of still images as depicting continuous motion. Recording only half of each still image works fine when the resulting video recording is played back, but each individual frame is usually extremely blurred. The image could be improved by merging together two successive frames, but because video records at a much lower resolution (that is, fewer pixels) than a typical still photograph, the result would still be of poor quality. To obtain the photograph-quality images admissible in court as evidence, Rudin and his Cognitech team used mathematical techniques to merge not two but multiple frames. Mathematical techniques were required because the different frames captured the action at different times; simply “adding together” all of the frames would produce an image even more blurred than any single frame.
The sequence of merged still images produced from the videotapes seemed to show Williams committing a number of violent acts, but identification was not always definitive, and as the defense pointed out, the enhanced images seemingly raised some issues. In one case, later images showed a handprint on the perpetrator's white T-shirt that was not visible on earlier images. This was resolved when a close examination of the videotape indicated the exact moment the handprint was made. More puzzling, earlier images showed a stain on the attacker's T-shirt that could not be seen on later images. On that occasion, targeted image enlargement and enhancement showed that in the later shots, the perpetrator was wearing two white T-shirts, one over the other, with the outer one hiding the stain on the inner one. (The enhanced image revealed the band around the bottom of the inner T-shirt protruding below the bottom of the outer shirt.)
Cognitech's video-processing technology also played a role in some of the other legal cases resulting from the riots. In one of them, the defendant, Gary Williams, pleaded guilty to all charges after the introduction into court of an enhanced ninety-second videotape that showed him rifling Denny's pockets and performing other illegal acts. Although Gary Williams had intended to plead not guilty and go for a jury trial, when he and his counsel saw the enhanced video, they acknowledged that it was sufficiently clear that a jury might well accept it as adequate identification, and decided instead to go for a plea bargain, resulting in a three-year sentence.
AND ON INTO THE FUTURE
With the L.A. riots cases establishing the legal admissibility of enhanced images, it was only a few weeks before Cognitech was once again asked to provide its services. On that occasion, they were brought in by the defense in a case involving an armed robbery and shooting at a jewelry store. The robbery had been captured by a surveillance camera. However, not only was the resolution low (as is often the case), the camera recorded at a low rate of one frame per second, well below the threshold to count as true video (roughly twenty-four frames per second). Rudin and his colleagues were able to construct images that contradicted certain testimony presented at trial. In particular, the images obtained showed that one key witness was in a room where she could not possibly have seen what she claimed to have seen.
Since then, Cognitech has continued to develop its systems, and its mathematical state-of-the-art Video-Investigator and Video-Active Forensic Imaging software suite is in use today by thousands of law enforcement and security professionals, and in forensic labs throughout the world, including the FBI, the DEA, the U.K. Home Office and Scotland Yard, Interpol, and many others.
In one notable case, a young African-American adult in Illinois was convicted (in part based on his own words, in part on the basis of videotape evidence) of the brutal murder of a store clerk, and was facing the death penalty. The accused and his family were too poor to seek costly expert services, but by good fortune his public defender questioned the videotape-based identification made by the state and federal forensic experts. The defender contacted Cognitech, which carried out a careful video restoration followed by a 3-D photogrammetry (the science of accurate measuring from photographs, using the mathematics of 3-D perspective geometry) of the restored image. This revealed an uncontestable discrepancy with the physical measurements of the accused. As a result, the case was dismissed and the innocent young man was freed. Some time later, an FBI investigation resulted in the capture and conviction of the real murderer.
Working with the Discovery Channel on a special about UFO sightings in Arizona (
Lights over Phoenix
), Cognitech processed and examined video footage to show that mysterious “lights” seen in the night sky were consistent with light flares used by the U.S. Air Force that night. Furthermore, the Cognitech study revealed that the source of the lights was actually behind the mountains, not above Phoenix as observers first thought.
Most recently, working on another Discovery Channel special (
Magic Bullet
) about the J.F.K. assassination, Rudin and his team used their techniques to solve the famous grassy knoll “second shooter” mystery. By processing the historic Mary Moorman photo with the most advanced image-restoration techniques available today, they were able to show that the phantom “second shooter” was an artifact of the photograph, not a stable image feature. Using advanced 3-D photogrammetric estimation techniques, they measured the phantom “second shooter” and found it to be three feet tall.
In an era when anyone with sufficient skill can “doctor” a photograph (a process that also depends on sophisticated mathematics), the old adage “photographs don't lie” no longer holds. But because of the development of image-reconstruction techniques, a new adage applies: Photographs (and videos) can generally tell you much more than you think.
