The Numbers Behind NUMB3RS (2 page)

The authors want to thank
NUMB3RS
creators Cheryl Heuton and Nick Falacci for creating Charlie Eppes, television's first mathematics superhero, and succeeding brilliantly in putting math on television in prime time. Their efforts have been joined by a stellar team of other writers, actors, producers, directors, and specialists whose work has inspired us to write this book. The gifted actor David Krumholtz has earned the undying love of mathematicians everywhere for bringing Charlie to life in a way that has led millions of people to see mathematics in a completely new light. Thanks also to
NUMB3RS
researchers Andy Black and Matt Kolokoff for being wonderful to work with in coming up with endless applications of mathematics to make the writers' dreams come true.

We wish to express our particular thanks to mathematician Dr. Lenny Rudin of Cognitech, one of the world's foremost experts on image enhancement, for considerable help with Chapter 5 and for providing the images we show in that chapter.

Finally, Ted Weinstein, our agent, found us an excellent publisher in David Cashion of Plume, and both worked tirelessly to turn a manuscript that we felt was as reader-friendly as possible, given that this is a math book, into one that, we have to acknowledge, is now a lot more so!

Keith Devlin, Palo Alto, CA

Gary Lorden, Pasadena, CA

On January 23, 2005, a new television crime series called
NUMB3RS
debuted. Created by the husband-and-wife team Nick Falacci and Cheryl Heuton, the series was produced by Paramount Network Television and acclaimed Hollywood veterans Ridley and Tony Scott, whose movie credits include
Alien
,
Top Gun
, and
Gladiator
. Throughout its run,
NUMB3RS
has regularly beat out the competition to be the most watched series in its time slot on Friday nights.

What has surprised many is that one of the show's two heroes is a mathematician, and much of the action revolves around mathematics, as professor Charlie Eppes uses his powerful skills to help his older brother, Don, an FBI agent, identify and catch criminals. Many viewers, and several critics, have commented that the stories are entertaining, but the basic premise is far-fetched: You simply can't use math to solve crimes, they say. As this book proves, they are wrong. You can use math to solve crimes, and law enforcement agencies do—not in every instance to be sure, but often enough to make math a powerful weapon in the never-ending fight against crime. In fact, the very first episode of the series was closely based on a real-life case, as we will discuss in the next chapter.

Our book sets out to describe, in a nontechnical fashion, some of the major mathematical techniques currently available to the police, CIA, and FBI. Most of these methods have been mentioned during episodes of
NUMB3RS
, and while we frequently link our explanations to what was depicted on the air, our focus is on the mathematical techniques and how they can be used in law enforcement. In addition we describe some real-life cases where mathematics played a role in solving a crime that have not been used in the TV series—at least not directly.

In many ways,
NUMB3RS
is similar to good science fiction, which is based on correct physics or chemistry. Each week,
NUMB3RS
presents a dramatic story in which realistic mathematics plays a key role in the narrative. The producers of
NUMB3RS
go to great lengths to ensure that the mathematics used in the scripts is correct and that the applications shown are possible. Although some of the cases viewers see are fictional, they certainly could have happened, and in some cases very well may. Though the TV series takes some dramatic license, this book does not. In
The Numbers Behind NUMB3RS
, you will discover the mathematics that can be, and is, used in fighting real crime and catching actual criminals.

Criminal Geographic Profiling

FBI Special Agent Don Eppes looks again at the large street map of Los Angeles spread across the dining-room table of his father's house. The crosses inked on the map show the locations where, over a period of several months, a brutal serial killer has struck, raping and then murdering a number of young women. Don's job is to catch the killer before he strikes again. But the investigation has stalled. Don is out of clues, and doesn't know what to do next.

“Can I help?” The voice is that of Don's younger brother, Charlie, a brilliant young professor of mathematics at the nearby university CalSci. Don has always been in awe of his brother's incredible ability at math, and frankly would welcome any help he can get. But…help from a mathematician?

“This case isn't about numbers, Charlie.” The edge in Don's voice is caused more by frustration than anger, but Charlie seems not to notice, and his reply is totally matter-of-fact but insistent: “
Everything
is numbers.”

Don is not convinced. Sure, he has often heard Charlie say that mathematics is all about patterns—identifying them, analyzing them, making predictions about them. But it didn't take a math genius to see that the crosses on the map were scattered haphazardly. There was no pattern, no way anyone could predict where the next cross would go—the exact location where the next young girl would be attacked. Maybe it would occur that very evening. If only there were some regularity to the arrangement of the crosses, a pattern that could be captured with a mathematical equation, the way Don remembers from his schooldays that the equation x
²
+ y
²
= 9 describes a circle.

Looking at the map, even Charlie has to agree there is no way to use math to predict where the killer would strike next. He strolls over to the window and stares out across the garden, the silence of the evening broken only by the continual
flick-flick-flick-flick
of the automatic sprinkler watering the lawn. Charlie's eyes see the sprinkler but his mind is far away. He had to admit that Don was probably right. Mathematics could be used to do lots of things, far more than most people realized. But in order to use math, there had to be some sort of pattern.

Flick-flick-flick-flick
. The sprinkler continued to do its job. There was the brilliant mathematician in New York who used mathematics to study the way the heart works, helping doctors spot tiny irregularities in a heartbeat before the person has a heart attack.

Flick-flick-flick-flick
. There were all those mathematics-based computer programs the banks utilized to track credit card purchases, looking for a sudden change in the pattern that might indicate identity theft or a stolen card.

Flick-flick-flick-flick
. Without clever mathematical algorithms, the cell phone in Charlie's pocket would have been twice as big and a lot heavier.

Flick-flick-flick-flick
. In fact, there was scarcely any area of modern life that did not depend, often in a crucial way, on mathematics. But there had to be a pattern, otherwise the math can't get started.

Flick-flick-flick-flick
. For the first time, Charlie notices the sprinkler, and suddenly he knows what to do. He has his answer. He could help solve Don's case, and the solution has been staring him in the face all along. He just had not realized it.

He drags Don over to the window. “We've been asking the wrong question,” he says. “From what you know, there's no way you can predict where the killer will strike next.” He points to the sprinkler. “Just like, no matter how much you study where each drop of water hits the grass, there's no way you can predict where the next drop will land. There's too much uncertainty.” He glances at Don to make sure his older brother is listening. “But suppose you could not see the sprinkler, and all you had to go on was the pattern of where all the drops landed. Then, using math, you could work out exactly where the sprinkler must be. You can't use the pattern of drops to predict forward to the next drop, but you can use it to work backward to the source. It's the same with your killer.”

Don finds it difficult to accept what his brother seems to be suggesting. “Charlie, are you telling me you can figure out where the killer lives?”

Charlie's answer is simple: “Yes.”

Don is still skeptical that Charlie's idea can really work, but he's impressed by his brother's confidence and passion, and so he agrees to let him assist with the investigation.

Charlie's first step is to learn some basic facts from the science of criminology: first, how do serial killers behave? Here, his years of experience as a mathematician have taught him how to recognize the key factors and ignore all the others, so that a seemingly complex problem can be reduced to one with just a few key variables. Talking with Don and the other agents at the FBI office where his elder brother works, he learns, for instance, that violent serial criminals exhibit certain tendencies in selecting locations. They tend to strike close to their home, but not too close; they always set a “buffer zone” around their residence where they will not strike, an area that is too close for comfort; outside that comfort zone, the frequency of crime locations decreases as the distance from home increases.

Then, back in his office in the CalSci mathematics department, Charlie gets to work in earnest, feverishly covering his blackboards with mathematical equations and formulas. His goal: to find the mathematical key to determine a “hot zone”—an area on the map, derived from the crime locations, where the perpetrator is most likely to live.

As always when he works on a difficult mathematical problem, the hours fly by as Charlie tries out many unsuccessful approaches. Then, finally, he has an idea he thinks should work. He erases his previous chalk scribbles one more time and writes this complicated-looking formula on the board: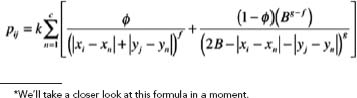
*

“That should do the trick,” he says to himself.

The next step is to fine-tune his formula by checking it against examples of past serial crimes Don provides him with. When he inputs the crime locations from those previous cases into his formula, does it accurately predict where the criminals lived? This is the moment of truth, when Charlie will discover whether his mathematics reflects reality. Sometimes it doesn't, and he learns that when he first decided which factors to take into account and which to ignore, he must have got it wrong. But this time, after Charlie makes a few minor adjustments, the formula seems to work.

The next day, bursting with energy and conviction, Charlie shows up at the FBI offices with a printout of the crime-location map with the “hot zone” prominently displayed. Just as the equation x
²
+ y
²
= 9 that Don remembered from his schooldays describes a circle, so that when the equation is fed into a suitably programmed computer it will draw the circle, so too when Charlie fed his new equation into his computer, it also produced a picture. Not a circle this time—Charlie's equation is much more complicated. What it gave was a series of concentric colored regions drawn on Don's crime map of Los Angeles, regions that homed in on the hot zone where the killer lives.

Having this map will still leave a lot of work for Don and his colleagues, but finding the killer is no longer like looking for a needle in a haystack. Thanks to Charlie's mathematics, the haystack has suddenly dwindled to a mere sackful of hay.

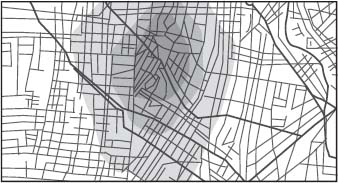
Charlie explains to Don and the other FBI agents working the case that the serial criminal has tried not to reveal where he lives, picking victims in what he thinks is a random pattern of locations, but that the mathematical formula nevertheless reveals the truth: a hot zone in which the criminal's residence is located, to a very high probability. Don and the team decide to investigate men within a certain range of ages, who live in the hot zone, and use surveillance and stealth tactics to obtain DNA evidence from the suspects' discarded cigarette butts, drinking straws, and the like, which can be matched with DNA from the crime-scene investigations.

Within a few days—and a few heart-stopping moments—they have their man. The case is solved. Don tells his younger brother, “That's
some formula
you've got there, Charlie.”

FACT OR FICTION?

Leaving out a few dramatic twists, the above is what the TV audience saw in the very first episode of
NUMB3RS
, broadcast on January 23, 2005. Many viewers could not believe that mathematics could help capture a criminal in this way. In fact, that entire first episode was based fairly closely on a real case in which a single mathematical equation was used to identify the hot zone where a criminal lived. It was the very equation, reproduced above, that viewers saw Charlie write on his blackboard.

The real-life mathematician who produced that formula is named Kim Rossmo. The technique of using mathematics to predict where a serial criminal lives, which Rossmo helped to establish, is called geographic profiling.

In the 1980s Rossmo was a young constable on the police force in Vancouver, Canada. What made him unusual for a police officer was his talent for mathematics. Throughout school he had been a “math whiz,” the kind of student who makes fellow students, and often teachers, a little nervous. The story is told that early in the twelfth grade, bored with the slow pace of his mathematics course, he asked to take the final exam in the second week of the semester. After scoring one hundred percent, he was excused from the remainder of the course.

Similarly bored with the typical slow progress of police investigations involving violent serial criminals, Rossmo decided to go back to school, ending up with a Ph.D. in criminology from Simon Fraser University, the first cop in Canada to get one. His thesis advisers, Paul and Patricia Brantingham, were pioneers in the development of mathematical models (essentially sets of equations that describe a situation) of criminal behavior, particularly those that describe where crimes are most likely to occur based on where a criminal lives, works, and plays. (It was the Brantinghams who noticed the location patterns of serial criminals that TV veiwers saw Charlie learning about from Don and his FBI colleagues.)

Rossmo's interest was a little different from the Brantinghams'. He did not want to study patterns of criminal behavior. As a police officer, he wanted to use actual data about the locations of crimes linked to a single unknown perpetrator as an
investigative tool
to help the police find the criminal.

Rossmo had some initial successes in re-analyzing old cases, and after receiving his Ph.D. and being promoted to detective inspector, he pursued his interest in developing better mathematical methods to do what he came to call criminal geographic targeting (CGT). Others called the method “geographic profiling,” since it complemented the well-known technique of “psychological profiling” used by investigators to find criminals based on their motivations and psychological characteristics. Geographic profiling attempts to locate a likely base of operation for a criminal by analyzing the locations of their crimes.

Rossmo hit upon the key idea behind his seemingly magic formula while riding on a bullet train in Japan one day in 1991. finding himself without a notepad to write on, he scribbled it on a napkin. With later refinements, the formula became the principal element of a computer program Rossmo wrote, called Rigel (pronounced RYE-gel, and named after the star in the constellation Orion, the Hunter). Today, Rossmo sells Rigel, along with training and consultancy, to police and other investigative agencies around the world to help them find criminals.