The Numbers Behind NUMB3RS (23 page)
Read The Numbers Behind NUMB3RS Online
Authors: Keith Devlin

A = area of the neutron detector = 0.3 square meters,
e = efficiency of the detector = 0.14,
S = neutrons emitted per second (depending on the source),
t = testing time = number of seconds the RPM is allowed to count the neutrons,
r
= distance from the RPM to the center of the container = 2 meters.
The result is:
Â
average number of neutrons counted = AeSt / 4?
r
2
.
Â
The variability of the number counted is described by a bell-shaped curve whose width (or standard deviation) is about 2.8 times the square root of the average. Since there is background radiation of neutrons at rate B, smaller than S, the background radiation is also described by a bell-shaped curve, which leads to a picture like this:
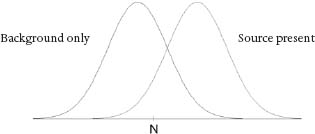
The threshold value N is the number of neutrons detected that call for another level of scrutinyâasking a human analyst to examine the scan produced by a VACIS gamma-ray-imaging system, which is designed to detect the kind of dense material in the container that would be used to shield emissions. If the person reading that scan cannot confirm the safety of the container, the truck is diverted to an offsite location where customs inspectors do a high-energy X-ray scan and, if necessary, open the container and inspect its contents manually. These inspections are a relatively costly part of the total system, but they can reliably detect radioactive material. Even if no containers exceed the RPM threshold, 5 percent of them can be expected to be flagged for VACIS inspection as untrusted containers by the automated targeting system, which uses a separate risk analysis of containers based on information about their origins.
Other key variables are the probabilities of success in the VACIS and X-ray scans and the costs include:
- $250 for each high-energy X-ray
- $1,500 for each opening of a container and manual inspection
- $100,000 for the annualized cost of each RPM machine
The objective of the entire analysis is to devise systems that for a given annual cost achieve the lowest possible detection limit:
Â
S
D
= source level of neutrons per second the RPM can detect
Â
with the requirement that the probability of the RPM detecting that source level must be at least 95 percent. False positivesâthat is, containers that produce a count at the level N or higher because of naturally occurring background radiationâare considered in the model, too, since they incur the costs of additional testing.
All things consideredâwithin a constraint on annual cost and the requirement not to slow down the flow of trucksâwhat can be done mathematically to improve the system? Wein and his coauthors analyze the existing design together with three possibly better ways to operate:
Design 1 = (existing) RPM at location A, 75 meters before front gate
Design 2 = RPM at the front gate, B
Design 3 = 4 RPMs, one at each lane-processing point
Design 4 = Add to Design 3 a row of 10 RPMs in the line in front of gate B
Under the quantitative assumptions of their paper, the OR mathematicians show that over a range of annual cost levels:
- Design 2 improves the detection limit S
D
by a factor of 2 with the same cost. - Design 3 improves S
D
by an additional factor of 4. - Design 4 improves S
D
by an additional factor of 1.6.
Thus, the overall improvement in going from Design 1, as used in the Hong Kong experiment, to Design 4 is a factor of 13 reduction in the source level of neutron radiation that the system can detect. How is this achieved?
The answer is in two parts. first is the fact that the longer the testing time, t, the greater the probability that we can correctly distinguish the presence of extra neutron emissions over the background. For the same reason that statisticians always recommend, if possible, taking a larger sample of data, a longer time for the RPMs to count neutrons effectively separates the bell-shaped curves so that they look more like this:
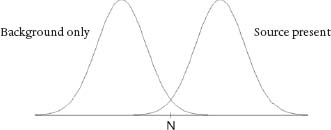
Since the two curves are now much less overlapped, the threshold value N used for detection can be set relatively lower without increasing the frequency of false positive detections. Alternatively, one can set the level of N so that false positives occur with the same frequency as before and successful detections occur when the source emissions, S, are lower. So the detection limit, S
D
, is reduced.
The second part of the authors' solution comes from the analysis of the queueing models for the four designs. The goal is to expose containers to longer testing times t. The potential for improvement is clear, since the RPM at point A gets only three seconds to look at each truck, whereas the trucks wait much longer than that to pass through the inspection process.
In moving the single RPM from A to B, Design 2 takes advantage of the fact that sometimes there are more trucks than usual flowing into the line, so that the line backs up, causing trucks to have to idle for a while in a line behind the front gate at B. So if the RPM is placed there, it will get a longer testing time on the trucks that have to wait.
In replacing the single RPM at B with four RPMs, one in each lane, Design 3 achieves an even greater improvement over Design 1, since the average processing time for the trucks to be cleared by the inspectors at the head of those lanes is sixty seconds. By using additional RPMs in a row before the front gate, B, Design 4 adds additional testing time, making possible a further reduction in the detection limit.
But what about the cost of all of those extra RPMs? Within any fixed annual budget, that cost can be offset by decreasing the frequency of false positives at each stage of the screening process, thereby reducing the cost of X-ray scans and manual inspections. The essence of an OR type of mathematical modeling and optimization (a mathematician's word for finding the best way) is that one has to determine which variables in a system should be adjusted to get better performance, while maintaining the constraints on other variables like the cost and the flow rate of trucks through the system. If he knew about the work of operations researchers like Wein, Liu, Cao, and Flynn, Charlie Eppes would be proud.
AIRLINE PASSENGER SCREENING SYSTEMS
Ever since the tragic events of September 11, 2001, the U.S. government has invested major financial and human resources in preventing such attacks from succeeding ever again. That attack intensified the government's efforts to enhance airline security through a system that had already been in place since 1998. Called CAPPS (for “computer assisted passenger prescreening system”), it relies on a passenger name record containing basic information obtained by the airline when a passenger books a ticketâname, address, method of paying for the ticket, and so on. The airline uses that information to make a check against the Transportation Security Administration's “no-fly list” of known or suspected terrorists and also to calculate a “risk score” based on terrorist profiles. These are lists of characteristics typical of terrorists, derived from statistical analysis of many years' worth of data on the flying habits of known terrorists. If a hit occurs on the no-fly list, or if the profile-based risk score is high enough, the airline subjects the passenger and his or her luggage to a more intensive, “second-level” screening than ordinary passengers undergo.
A similar system was instituted after a wave of skyjackings of commercial airliners in the years 1968 and 1969 (when there were more than fifty such events) led to the development of a “skyjacker profile” that was used for several years and then discontinued. Though the specific elements of both the skyjacker profile and the terrorist profile are closely guarded secrets, a few of their features have frequently been surmised in public discussions. (For instance, if you are a young man traveling alone, it would be better not to buy a one-way ticket, particularly if you pay for it with cash.)
After 9/11, the newly formed Transportation Security Administration assumed responsibility not only for a “no-fly list” but for the statistical analyses needed to design more effective profiles of terrorists. Experts outside the government believe that the TSA is using neural nets (see Chapter 3) to refine the terrorist profile. There is no doubt that it seems like good common sense for federal authorities to try to separate out from the general population those airline passengers who could be considered high risk as potential terrorists, and then subject them to greater scrutiny and search. That is the logic of CAPPS. But how well can such a system be expected to work? The answer, as we shall see, is not as simple as it might at first appear.
TWO MIT STUDENTS USE MATHEMATICS TO ANALYZE CAPPS
In May 2002, a pair of graduate students at MIT made national news by announcing a paper they had prepared for a class called “Ethics and Law in the Electronic Frontier.” Samidh Chakrabarti and Aaron Strauss thought that analyzing CAPPS would make an interesting paper for the class, and the results of their mathematical analysis were so striking that the professor urged them to publish them more widely, which they proceeded to do on the Internet. Their paper “Carnival Booth: An Algorithm for Defeating the Computer-Assisted Passenger Screening System” caused a sensation because it showed by clear logic and mathematical analysis how terrorists could rather easily adapt their behavior to render CAPPS less effective than pure random selection of passengers for second-level screening.
The two authors assume that
- No matter which system is used to select passengers for second-level screening, only 8 percent of them can be handled in that way.
- In CAPPS, the federal requirement to randomly select “x percent of passengers” for second-level screening is met by randomly selecting 2 percent.
- Three out of every four terrorists assigned to secondary screening will be successfully intercepted.
- If they are not assigned to secondary screening, only one out of every four terrorists will be successfully intercepted.
- The percentage of terrorists who are not randomly selected for secondary screening but will be flagged by CAPPS is unknown. Call it
p
percent.
These percentage assumptions made by Chakrabarti and Strauss are not random. Rather, they based their analysis on the publicly available best estimates of the actual percentages, which are a government secret. Their results do not depend substantially on the exact values of those percentages. The unknown percentage
p
depends on how high a risk score is required to assign a passenger to secondary screening. To meet the requirement of “no more than 8 percent” for secondary screening, the threshold for the risk score will have to be chosen so that it is achieved by 6 percent of the nonterrorist passengers who escape random selection.
Then, the overall percentage of terrorists who will be intercepted under CAPPS is:
Â
(*) ¾ of
p
% + ¾ of 2% + ¼ of the remaining percentage
Â
For comparison, Chakrabarti and Strauss consider a “pure chance” system, in which the 8 percent of passengers that can be handled in secondary screening are chosen at random from the list of all passengers. In that case the overall percentage of terrorists who will be intercepted is:
Â
(**) ¾ of 8% + ¼ of 92% = 6% + 23% = 29%
