The Numbers Behind NUMB3RS (25 page)

 

1/150 × 1/8 = 1/(150 × 8) = 1/1200

 

which is considerably larger than 1/30,000.

The number used for illustration here, 1/8, is called the “conditional probability” that a car is lowered, given that it is a black Honda Civic. Obtaining reliable data to determine that number, or at least to estimate it accurately, is likely to be more difficult than just estimating the fraction of
all
cars that have been lowered—the “1 out of 200” in the original calculation. But surely, in any serious endeavor—in particular, a criminal trial—the fact that a number is hard to determine or estimate is no excuse for making a highly dubious assumption, such as independence. The potential for error is compounded when we pile up a whole list of features (six in the Collins case) and assume that they are all independent. Even Charlie Eppes would be hard-pressed to come up with the right data and calculate an accurate estimate of the probability that a couple who commit a crime in Los Angeles would have those six characteristics.

Yet that was not the last of the errors the original trial court made. The most devastating blow that the Supreme Court struck in its reversal of Collins' conviction concerned a mistake that (like the unjustified assumption of independence) occurs frequently in the application of probability and statistics to criminal trials. That mistake is usually called “the prosecutor's fallacy.”

This notorious fallacy consists of a sort of bait-and-switch tactic by the prosecution, sometimes made because of unintentional error. On the one hand, we have the prosecution's calculation, which in spite of its lack of justification, attempts to determine

Ignoring the defects of the calculation, and assuming for the sake of argument that P(match) truly is equal to 1 in 12 million, there is nevertheless a profound difference between P(match) and

 

P(innocence) = the probability that the Collinses are innocent.

 

As the Supreme Court noted, the prosecutor in the Collins case argued to the jury that the 1 in 12 million calculation applied to P(innocence). He suggested that “there could be but one chance in 12 million that defendants were innocent and that another equally distinctive couple actually committed the robbery.”

The confusion between these two probabilities is wrong and dangerous! P(match) is trying to calculate the probability that the defendants,
if they are innocent,
would be unlucky enough to match the witness descriptions of the couple who committed the robbery. But as the justices explained in their opinion, a “probability of innocence” calculation (even if one could presume to actually calculate such a thing) has to take into account how many other couples in the Los Angeles area also have these six characteristics. The court said, “Of the admittedly few such couples, which one, if any, was guilty of committing the robbery?”

In a master stroke that warmed the hearts of mathematicians and statisticians around the world when we subsequently read about the Collins case, the court's opinion went on to add an appendix in which they calculated another estimate. Even taking the prosecution's 1 in 12 million result at face value, what is the probability that somewhere in the Los Angeles area there are at least two couples who have the six characteristics as the witnesses described for the robbers? The justices estimated that probability by assuming that there are a large number N of possible perpetrators—pairs of people (not necessarily “couples”) in the Los Angeles area—and that each pair has a probability of 1 in 12 million of fitting the robbers' descriptions. Using their own independence assumption about different pairs fitting the description (which is not exactly right but is not a source of substantial error), they performed a calculation using the binomial distribution.

Imagine flipping N coins, they reasoned, each with probability 1 in 12 million of turning up heads. Given that at least one coin turns up heads (meaning that there is at least one couple that meets the description), what is the probability that two or more heads occur—that there are at least two couples that meet the description?

The answer to the question is easy to calculate using the binomial distribution (a calculator or spreadsheet can be used), and not surprisingly it depends on N—the number of potential “perpetrator couples”. For illustration, the court used N = 12 million, approximately the number of people in the Los Angeles area at the time, and they calculated that the answer is “over 40 percent.” (It's actually 41.8 percent.) In this way, they argued that it is not at all reasonable to conclude that the defendants must be guilty simply because they have the six characteristics in the witnesses' descriptions.

Of course, a different choice of N would give a different answer, but even N = 3 million, say, would yield a probability of 12 percent that somewhere in Los Angeles there exists at least one other pair who arguably would be as good candidates for conviction as the Collinses—at least in terms of the “proof by mathematics” that the prosecution relied on to sway the jury. That hardly sounds like “beyond a reasonable doubt,” does it?

The key fact the prosecutor's fallacy overlooks is that there are typically many other people (or couples) not on trial who have the calculated probability (like 1 in 12 million) of matching the accused person (or couple). Therefore, even if those on trial are innocent, there is typically a far larger probability than P(match) of their being unlucky enough to match the characteristics being used to identify the perpetrators of the crime.

The Collins case may have become a famous example in legal circles, but it was by no means the first time in U.S. legal history that a trial was decided almost entirely on mathematics. In the Collins case, the use made of mathematics turned out to be incorrect. But things came out very differently in an equally famous case a hundred years earlier.

FAMOUS NINETEENTH-CENTURY MATHEMATICIANS DEMONSTRATE A FORGERY

One of the most famous American forgery cases, a cause célèbre in the nineteenth century, hinged upon key testimony of father-and-son mathematicians. Benjamin Peirce was one of the leading mathematicians of his day, a famous professor at Harvard University, whose name is still used to bestow honor upon young mathematicians who are appointed Benjamin Peirce Assistant Professors at Harvard. His son, Charles Sanders Peirce, was also a brilliant scholar who taught mathematical logic, worked for the U.S. Coast and Geodetic Survey, the leading federal agency in the funding of nineteenth-century scientific research, and wrote prodigiously in the field of philosophy, becoming best known as the founder of “American pragmatism.”

What kind of trial would bring both of the Peirces into the courtroom as expert witnesses? It was a forgery trial involving the estate of Sylvia Ann Howland, valued at $2 million when she died—a huge figure back in 1865. Her niece, Hetty Howland Robinson, contested the will, which left her only a part of the estate, and claimed that she and her aunt had a secret agreement under which Robinson would inherit the entire estate. As proof she presented an earlier version of the aunt's will that not only left the entire estate to her but also contained a second page declaring that any later wills should be considered invalid! The executor of the estate, Thomas Mandell, rejected Robinson's claim on the basis that the second page was a forgery, and therefore the later will should determine the disposition of the estate.

Robinson was never charged with the crime of forgery. In fact, the sensational case that ensued,
Robinson v. Mandell
, popularly known as the Howland will case, resulted from Robinson's filing of a lawsuit in an attempt to overturn the executor's rejection of her claim! And this was the lawsuit that was decided using mathematics.

In most forgery cases, someone attempts to duplicate the signature or handwriting of person X, and prosecutors (or civil litigators) try to demonstrate in court the dissimilarity of the forgeries from samples of the authentic writing of X. But in the Howland will case the issue was the reverse: The forgery was simply too good!

Benjamin and Charles Peirce were called as witnesses for the defendant Mandell to testify about their careful scientific investigation of the similarity between the authentic signature on the first page and the disputed signature on a second page. (There were actually
two
second pages, but only one was analyzed.)

Here are the two signatures.

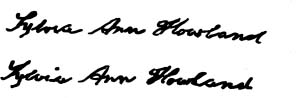
If you look at two copies of your own signature you will soon notice some differences between them. The two signatures on the Howland will, however, look identical. The most likely explanation is that one is a traced copy of the other.

What the Peirces did was turn this suspicion into a scientific fact. They devised a method to compare and express the agreement between any two signatures of the aunt as a number—a sort of score for closeness of agreement. To determine this score, they decided to use downstrokes—there are thirty of them in each signature—and to count the number of “coincidences” between the thirty downstrokes in one signature and the corresponding thirty downstrokes in the other. By a “coincidence” between two examples of a particular downstroke, such as the downstroke in the first letter “L”, they mean an essentially perfect match between those strokes, which they judged by overlaying photographs of the signatures, one on top of the other.

When they compared the two signatures shown above, they found that every one of the thirty downstrokes coincided! Could this be due to sheer chance? Or was it clear evidence that the disputed signature was obtained by tracing the authentic signature onto the disputed second page? That's where the mathematical analysis came in.

The Peirces obtained a set of forty-two undisputed authentic signatures of Sylvia Ann Howland. For forty-two signatures there are 42 × 41/2 = 861 ways to select a pair of signatures to compare. For each of these 861 pairs they determined the number of coincidences—how many of the thirty downstrokes coincided? They found a total of 5,325 coincidences among the 861 × 30 = 25,830 comparisons of downstrokes. That meant that about one out of five comparisons was judged a coincidence—a perfect match.

The rest of their analysis was mathematical, or more specifically, statistical. The elder Peirce described his calculation of the chances of getting thirty coincidences out of thirty downstrokes, assuming that each occurred with probability 5325/25830 = 0.206156. Assuming these coincidences occur independently (!), Peirce used the product rule to multiply, giving

 

.206156 × .206156 × .206156 ×…[30 times]

 

i.e.,

.206156
³⁰
.

This figure is approximately 1 in 375 trillion. (Peirce actually made a mistake in his calculation, and gave a somewhat larger number, using 2,666 in place of 375.)

Summoning the full eloquence expected of a gentlemanly mathematician in 1868, Professor Peirce summarized his findings in this way: “So vast improbability is practically an impossibility. Such evanescent shadows of probability cannot belong to actual life…. The coincidence which has occurred here must have had its origin in an intention to produce it.”

Surely not surprising in light of this mathematical and rhetorical splendor, the court ruled against Hetty Robinson.

What would a modern mathematician—or statistician—say about Professor Peirce's analysis? The data for the 861 comparisons of pairs of signatures—counting the number of coincidences—can be analyzed to see how well the independence assumption is satisfied, or the binomial model that it leads to, and the result is that the data counting coincidences for those 861 pairs do
not
fit Peirce's model very well at all. But that does not mean that his conclusion that the thirty coincidences on thirty downstrokes is highly unusual cannot be sustained. As pointed out by Michael O. finkelstein and Bruce Levin in discussing the Howland Will Case in their excellent book
Statistics for Lawyers,
statisticians nowadays would typically prefer to analyze such data in a “nonparametric” way. This means the analysis does not assume that when two signatures are compared, the probabilities of zero coincidences, one coincidence, two coincidences, and on up to thirty coincidences, are known to satisfy some particular formulas or, if expressed in a bar chart, to have some particular shape.