The Physics of Superheroes: Spectacular Second Edition (43 page)

Amazed that, unlike all previous attempts, he was able to successfully change the course of history, Superman decides to make various pit stops on his return trip to his own time period, using this opportunity to “fix” various historical events. He saves the Christians from being eaten by lions in the Roman Colosseum,
⁷⁵
takes Nathan Hale’s place as he is about to be executed by the British, prevents Custer’s massacre at Little Big Horn, and drops by Ford’s Theater on April 14, 1865. As shown in fig. 32, as John Wilkes Booth is about to assassinate President Lincoln, he utters “Sic semper—Ulp!” as hands that can crush diamonds close upon his pistol. Superman is now like a kid in a historical candy store, and decides to try to save the population of his home planet, Krypton. Because he loses his superpowers under the red light of Krypton’s sun, Rao (by this time the explanation for his amazing abilities had been attributed to Earth’s yellow sun), Superman decides to build a fleet of spaceships from sunken Earth naval vessels and send them to Krypton in order to enable everyone to escape to another world. Using his telescopic vision, he watches his parents disembark on a new planet with an infant Kal-El. At this point Superman realizes that he has stumbled upon a paradox, for if his parents never sent him to Earth as a baby, how is he able to save them now?

Returning to his present, in 1961, the Man of Tomorrow is sur prised to discover that history books are unchanged, shown in fig. 33. Lincoln was indeed shot at Ford’s Theater and Nathan Hale and General Custer are similarly described suffering their Superman-less fates. Superman can’t understand how this can be, since “surely, the [history] books are truthful.” Ahem. Retracing his path through the time stream, Superman comes across an alternate Earth (fig. 34), in which the history books give proper credit to Superman’s role in correcting the past’s “mistakes.”

Alas, Superman discovered in 1961 what theoretical physicists have rediscovered in 2001—that time travel is only possible via the many-worlds interpretation of quantum mechanics. Superman did indeed accomplish these amazing feats, altering the course of history—but in an alternate universe, not in his own (see fig. 34). A similar phenomenon occurs in the Marvel Comics
Avengers # 267,
where the evil time lord Kang the Conqueror is revealed to have single- handedly created a vast number of alternate Earths as a by-product of his frequent time-traveling in order to defeat his superhero foes. Still another example of comic books being ahead of the physics curve.

23

THROUGH A WALL LIGHTLY—
TUNNELING PHENOMENA

IN ADDITION TO BEING ABLE to run at amazing speeds, the Flash is said to possess total control over every one of his molecules’ motions. This vibratory control was put to use in
Flash # 116, Flash # 123
(see fig. 30), and many times since. Matching his body’s vibrations to the vibrational frequency of the atoms in a wall, it was argued by the writers of Flash comics that he could pass through a solid wall without harm to either himself or the wall. However, it is not true that the only reason we cannot walk through solid walls is that we vibrate at a different frequency than the atoms in the wall. As discussed earlier, the average rate at which our atoms vibrate is simply a reflection of our temperature. Our bodies are typically roughly within 40 percent of the temperature of a wall, so our atoms’ vibrational frequency is already pretty well matched to those in the wall.

Nevertheless, there is a quantum mechanical phenomenon termed “tunneling” that predicts that an object, under the right circumstances, can pass through a solid barrier without disturbing either the barrier or itself. This very strange prediction is no less weird for being true. In this way quantum mechanics informs us that electrons are a lot like Kitty Pryde of the X-Men, who possesses the mutant ability to walk through solid walls (as shown in fig. 35), or the Flash.

Schrödinger’s equation enables one to calculate the probability of an electron moving from one region of space to another even if common sense tells you that the electron should never be able to make this transition. Imagine that you are on an open-air handball court with a chain-link fence on three sides of the court and a concrete wall along the fourth side. On the other side of the concrete wall is another identical open-air court, also surrounded by a fence on three sides and sharing the concrete wall with the first court. You are free to wander anywhere you’d like within the first court, but lacking superpowers, you cannot leap over the concrete wall to go to the second court. If one solves the Schrödinger equation for this situation, one finds something rather surprising: The calculation finds that you have a very high probability of being in the first open-air court (no surprise there) and a small but nonzero probability of winding up on the other side of the wall in the second open-air court (huh?). Ordinarily the probability of passing through a barrier is very small, but only situations for which the probability is exactly zero can be called impossible. Everything else is just unlikely.

Fig. 35.
A scene from
X-Men # 130,
showing Kitty Pryde (not yet a member of the X-Men) as she employs her mutant ability to walk through walls to sneak up on the White Queen of the Hellfire Club.

This is an intrinsically quantum mechanical phenomenon, in that classically there is no possible way to ever find yourself in the second court. This quantum process is called “tunneling,” which is a misnomer, as you do not create a tunnel as you go through the wall. There is no hole left behind, nor have you gone under the wall or over it. If you were to now run at the wall in the other direction, it would be as formidable a barrier as when you were in the first open-air court, and you would now have the same very small probability of returning to the first court. But “tunneling” is the term that physicists use to describe this phenomenon. The solutions of Schrödinger’s equation that predict tunneling phenomena find that the faster you run at the wall, the larger the probability you will wind up on the other side, though you are not moving so quickly that you leap over the wall. This is no doubt how the Flash, both the Golden and Silver Age versions, is able to use his great speed to pass through solid objects, as shown in fig. 36. He is able to increase his kinetic energy to the point where the probability, from the Schrödinger equation, of passing through the wall becomes nearly 100 percent.

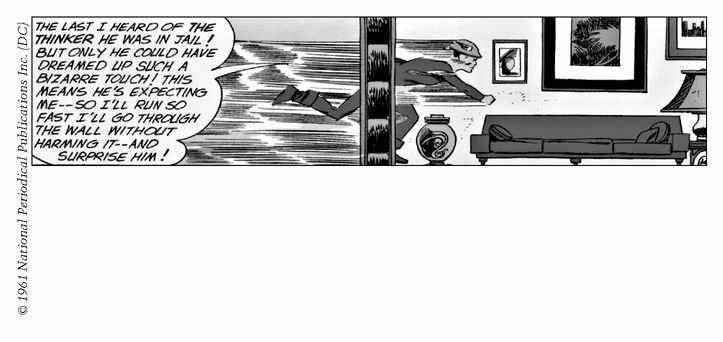
Fig. 36.
Scene from
Flash # 123,
where Jay Garrick, the Golden Age Flash, demonstrates the quantum mechanical process known as “tunneling.” The matter-wave of an object has a small but nonzero chance of passing through a solid barrier. The faster the object approaches the barrier, the greater the transmission probability. As Jay correctly notes, the barrier is unaffected by the tunneling process.

Consider two metals separated by a vacuum. An electron in the metal on the left is like a person in the first open-air handball court. Instead of a concrete wall, a thin vacuum separates this electron from the second metal, which can be considered another open-air court. Solving the Schrödinger equation for this situation, one finds that the electron in one metal has a small but nonzero probability of finding itself in the second metal. The electron does not arc across the vacuum gap and does not have enough kinetic energy to escape from the metal on its own. (This is a good thing. Otherwise, all objects would be continually leaking electrons all over the place, and static cling would be one the most gripping problems of the day.) Rather, the electron’s matter-wave extends into the separation space, decreasing in magnitude with distance in the gap. A similar phenomenon occurs with light waves moving from a denser to a less-dense medium. Under conditions for which the light wave should be totally reflected at the interface, there is still a small diffraction of light into the less-dense medium. The diffracted wave’s magnitude decreases the further into the less-dense medium it progresses. Since the square of the electron’s wavefunction represents the probability of finding the particle at a point in space and time, a finite magnitude for the “ matter-wave” indicates that there is a nonzero probability that the electron will be found in the second metal. If the gap is not too large (compared with the electron’s matter wavelength, which in practice means roughly less than one nanometer), then the matter-wave will still have an appreciable magnitude in the second metal. Let us be clear, the electron on one side of the barrier moves toward the obstruction, and most times simply reflects off the wall. If a million electrons strike the barrier then, depending on its height and width, 990,000 electrons might be reflected and 10,000 would wind up on the other side.