The Unimaginable Mathematics of Borges' Library of Babel (33 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

4.
Etc.
If this hexagon-visiting algorithm
is carried out, it is not hard to see that at any stage, only a finite number
of hexagons have been visited, and a traveler granted infinite time must
eventually visit every single hexagon. This last assertion follows because even
if the Library extends infinitely in all directions, it still must be the case
that any hexagon in the Library is fixed at a finite number of hexagons from
the Origin—the hexagon in which the traveler began.

Although he never explicitly
mentions "The Library of Babel," I include a discussion of Svend Østergaard
because I believe the book proposed in the final footnote of "The Library
of Babel" is of a similar structure to the book described in Borges' short
story "The Book of Sand." In
The Mathematics of Meaning,
Østergaard
discusses the Book of Sand, but proceeds under the unwarranted assumption that
it possesses uncountably infinitely many pages.
2
I find it
unlikely that there are uncountably many pages, for the narrator of "The
Book of Sand" only mentions the finding of integer-numbered pages: if that
was so, it would be extraordinary to find even a single page numbered by an
integer, because the likelihood of randomly finding an integer in the real
number line is
zero
—or if that sounds improbably absolute,
"vanishingly small." This is because the set of integers is countable
and therefore, when considered as a set contained inside of the real numbers,
it is of measure 0. This entails that any integer is much harder to find than a
single prespecified dust speck adrift in South America. (See my second
interpretation of the Book of Sand in the chapter "Real Analysis" for
a discussion on measure 0.)
This is
essentially the reason that while the narrator for "The Book of Sand"
is looking at a particular page, the mysterious stranger adjures him to
"Look at it well. You will never see it again." The probability of
randomly picking the same integer twice is also vanishingly small. To see this,
imagine opening the Book of Sand to page 17. If there were only 100 pages in
the Book, each time it was opened again there would be a 1/100 chance of
randomly opening it to page 17. If there were 1,000 pages, there would be a
1/1,000 chance. If there were a million pages, there would be a 1/1,000,000
chance. If there were infinitely many pages, it is tempting to write that there
would be a 1/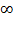 chance, meaning "probability 0." But it wouldn't be
chance, meaning "probability 0." But it wouldn't be
correct to write that, and the story of the probability, while interesting and
exciting, is beyond the scope of this book. (If the stranger and narrator were
truly interested in seeing a page a second time, it's fair to wonder why they
didn't simply insert a cardboard bookmark to reenter this bookish Heraclitean
river twice.)
Moreover,
the narrator of "The Book of Sand" states that illustrations occur
every 2,000 pages. If there were uncountably many pages—that is, the same
number of pages as there are of points in the real number line— then there
would be no way of counting the number of pages between two selected pages. In
fact, there'd be no way to find a "next page," for in the real number
line, numbers lap up against each other with no "closest" number.
This is known, in various guises, as the
Archimedean property.

I have great sympathy for the
last two critics I'm going to discuss, N. Katherine Hayles and Merrell; their
project, as I understand it, is truly noble. They seek to create or expand upon
a theory which accounts for all the complex interrelations between the
perceivable universe, consciousness, all previous and current human works, the
Zeitgeist, culture, language, author, text, interpretation, and reader. Such a
theory would, by virtue of absorption, dwarf a Grand Unified Theory of
Everything from physics. It is natural, therefore, that two literary critics,
steeped in the disciplines of chemistry and physics, would appropriate the
language and approaches of mathematics and science to employ them in this most
ambitious theory.
Hayles' work
(Hayles, 138—67) primarily consists of associating ideas of self-referentiality
and infinite sequences, infinite series, and infinite sets to Borges' work.
Many of her insights are deep. Although some passages seek to persuade the
reader of the meaninglessness and marginalization of mathematics, Hayles is
content to use mathematics as a means for understanding Borges, perhaps in the
same way a sponge, riddled with holes, is useful in sopping up fluid reality.
After a précis
of the story, on page 151 Hayles critiques the librarian's "elegant
hope" by noting that "the narrator's 'solution' is of course an
answer only in a very narrow sense. While it suggests a way to transform
randomness into ordered sequence, it contains no hint of how that sequence may
be rendered intelligible or meaningful." As I noted in the chapter "Topology
and Cosmology," the patterning of a periodically repeating Library may be
thought of as symmetric three-dimensional wallpaper. For example, the
illustration in figure 67 is, in some sense, random and chaotic. However, when
it repeats periodically, it takes on a pleasant enough symmetry; an order, if
you will (figure 68). I contend again that this is the Order that in-formed the
narrator's out-look.

Hayles' main intent, in her
reading of "The Library of Babel," is poetic: she wants a Borgesian
"Strange Loop" to dissolve the boundary between the reader and the
text by roping the reader into the story itself. However, to accomplish this
lyrical agenda, Hayles writes on page 152 that "Logic demands that we
conclude the present text in hand (which of course is printed) to be the
Library's book. What we have is not the narrator's handwritten text but a
mirror of it, or perhaps one of the 'several hundreds of thousands of imperfect
facsimiles."' It is curious that a critic eager to limit logic should
invoke it almost as a magic amulet, for "logic" doesn't
"demand" anything. Rather, it seems to me that Hayles is attempting
to have her theory of Strange Loops produce a variation of a result that Borges
himself stresses in the story, "This useless and wordy epistle already
exists in one of the thirty volumes of the five shelves in one of the
uncountable hexagons—and so does its refutation." The story is in the
Library, the book it originally appeared in,
Ficciones,
is in the
Library, and the complete works of Borges are in the Library. Hayles' books,
the words of this book, and anything that can be written using 25 orthographic
symbols: all are necessarily in the Library. Nevertheless, none of these
inclusions implies that we are at this moment reading a Library book or that we
are librarians roaming a universe of hexagons.

If
we can legitimately
assume
as a
premise
that we are
holding a Library book in our hands, then Hayles' next set of ideas, which are
intriguing, do follow: "... even more important is the implication that we
are reading the Library's book. This, in turn, implies that we, like the
narrator, are within the Library examining one of its volumes, which means that
we, no less than the narrator, are contained within one of the books we
peruse." Since the premise is unfounded—my copy of
Ficciones
is not
410 pages, I'm not in a dimly lit hexagon—the chain of implications does not
follow.
3
If, on the
other hand, Hayles was referring to a sort of narratological space created by
the story, where we readers accept that by virtue of reading the story we are
somehow in the story's confines, then it still doesn't follow that we are
reading a printed text of the Library rather than a handwritten note of an
avuncular librarian. In fact, given that we are human, inhabiting a miniscule
section of the Library where humans reside, it is vastly more likely that we
would stumble across a book which a human has inscribed than one which contains
the story "The Library of Babel."
The story,
including spaces, is comprised of approximately 18,000 lexical symbols. These
contiguous 18,000 symbols could occupy 1,294,001 different starting positions
in a 410-page book. To see this, observe that the first such position would
entail that the first symbol of the story occupied the first slot of the book's
1,312,000 slots. The last such position has the concluding period of the story
occupying the last slot in the book. This entails that the first symbol of the
story occupies the 1,294,000th slot. It may be helpful to visualize this
process as a block of 18,000 red squares moving along a tape of 1,312,000
slots. If the first red square is at the first slot, then the last red square
is at the 18,000th slot. If the last red square is at the last slot, then the
first red square is at the [(1,312,000 — 18,000) + 1]th slot.
