The Unimaginable Mathematics of Borges' Library of Babel (36 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Many commentators have pointed
towards Borges' amiable review of Kasner and Newman's
Mathematics and the Imagination
as an indication of his interest in mathematics and also as a source of his
knowledge. Unfortunately, it was not among the books from his personal library
that were donated to the National Library. However, I was able to obtain a copy
elsewhere and give it a professional reading. (An evocative aspect of the book
is that the cover, as opposed to the dust jacket, is embossed with an
aleph-nought,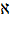 0
0
, which was Cantor's symbol
for a countably infinite set.
4
) Borges' review,
reprinted in
Selected Non-Fictions,
notes that the book includes
. .. the
endless map ofBrouwer,
5
the fourth dimension glimpsed by More and which Charles Howard
Hinton claims to have intuited, the mildly obscene Möbius strip, the rudiments
of the theory of transfinite numbers, the eight paradoxes of Zeno, the parallel
lines of Desargues that intersect in infinity, the binary notation Leibniz
discovered in the diagrams of the
I Ching,
the beautiful Euclidean
demonstration of the stellar infinity of the prime numbers, the problem of the
tower of Hanoi, the equivocal or two-pronged syllogism.
Most surprising to me, given
that many today attribute an interest in
fractals
to Borges, is that
Kasner and Newman's book examines the famous Koch snowflake curve in some depth
on pages 344—55. The snowflake curve is a standard introductory example of a
fractal—and for historical context, I mention that Kasner and Newman's
discussion precedes the term "fractal" by almost 40 years.
Apparently, though, Borges was sufficiently unimpressed by the snowflake curve
that he neglected to mention it in his review.
Perhaps
Borges found the anti-Nazi gibes another appealing facet of the book, given his
own strong—and unpopular—anti-Nazi stance during World War II. Despite these
many commendable contents and qualities, given that the book was published in
1940, it seems unlikely that it was available for his consultation and
degustation prior to the writing of "The Library of Babel."
There are at
least two candidates from Borges' personal library to which it is tempting to
assign influential status in the development of his mathematical thought. The
first is Henri Poincaré's 1908 book
Science et Méthode.
Borges' end leaf
notations, dated 1939, indicate an interest in Lesage's discredited theory of
gravitation and, more tellingly, in geometry and Cantor. One paragraph, taken
from pages 380—81, is a passage on geometry worth quoting (emphases added):
A great
advantage of geometry lies in the fact that in it the senses can come to the
aid of thought, and help find the path to follow, and many minds prefer to put
the problems of analysis into geometric form. Unhappily, our senses can not
carry us very far, and they desert us when we wish to soar beyond the classical
three dimensions.
Does this mean, beyond the restricted domain wherein they
seem to wish to imprison us, we should rely only on pure analysis and that all
geometry of more than three dimensions is vain and objectless?
[.. . ] We
may also make an
analysis situs
of more than three dimensions. The
importance of
analysis situs
is enormous and can not be too much
emphasized; the advantage obtained from it by Riemann, one of its chief
creators, would suffice to prove this. We must achieve its complete
construction in the higher spaces;
then we shall have an instrument which
will enable us really to see in hyperspace and supplement our senses.
Again, I don't imagine that
Borges considered exotic cosmologies for the Library, but it interests me to
think that he was aware of things living in higher-dimensional spaces.
The sections
pertaining to Cantor mainly restrict themselves to exuberant denunciations of
set theory via what Poincaré terms "the Cantorian
antinomies"—paradoxes arising from Cantor's theory of transfinite numbers.
In many ways, Poincaré prefigures a movement towards constructivism in
mathematics, which I briefly discuss in the Math Aftermath "Libits, Uniqueness,
and Jumping from the Finite to the Infinite." Since Borges was evidently
fascinated by transfinite numbers and the concept of infinity, it's striking
that as an autodidact, he pursued the arguments and weighed the objections of Poincaré,
a formidable opponent of all things infinite.
The other
book from Borges' library, philosophically opposed to Poincaré's, is Bertrand
Russell's
Principles of Mathematics.
The book was originally published
in 1903, and Borges' copy is a 1938 printing. Borges dated his copy
"1939," and his annotations further indicate that it was a gift from
"Adolfo" (presumably his life-long friend, colleague, and coauthor
Bioy Casares). The easiest opening of this volume, and the first page singled
out by Borges, concerns a resolution of Parmenides' paradox. The next page
pleasantly segues into a discussion of Zeno's paradox of Achilles and the
tortoise. The argument contained therein is similar to Russell's refutation in
Mathematical Philosophy,
which Borges outlined in his 1929 essay "The
Perpetual Race of Achilles and the Tortoise." Indeed, Borges' annotation
includes the phrase "(cf.
Mathematical Philosophy,
138)."
Borges'
essay on Zeno's paradox not only betrays a fondness for and knowledge of
Cantor's transfinite numbers; it also demonstrates that Borges understood at
least the basics of summing infinite series. That Borges persisted in using
Russell as a mathematical touchstone is further evidenced by the brilliant 1939
essay "When Fiction Lives in Fiction," which appears in
Selected
Non-Fictions,
pages 160—62. Here, Borges writes
. . .
Fourteen or fifteen years later, around 1921, I discovered in one of Russell's
works an analogous invention by Josiah Royce, who postulates a map of England
drawn on a portion of the territory of England: this map—since it is exact—must
contain a map of the map, which must contain a map of the map of the map, and
so on to infinity. . .
Principles of Mathematics
is rife with Russell's perspectives on Cantor, transfinite
numbers, infinitesimals, the meaning of zero, and a host of other Borgesian
obsessions. Despite his cavil found on page 46 of
Selected Non-Fictions
that some of Russell's works are "unsatisfactory, intense books, inhumanly
lucid," Borges returned to them again and again. Russell's book, although
dry, discursive, and monolithic in conception and execution, contains poetic
phrases, one of which Borges singled out with an end leaf notation:
...
the
infinite regress is harmless.
A point needs to be stressed.
Mathematics is a body of lore and an art that requires years of study and
practice to understand and appreciate. Just as with twentieth-century atonal
music, repeated exposure is required to acculturate the novice to the
aesthetics of beauty and elegance particular to mathematics. Grappling with
problems and attempting to produce one's own proofs using the licit logical
structures are essential to internalize an understanding of the many subtleties
inherent in mathematics. I contend that, in this sense, Russell's books are
not
mathematics; rather they are the
philosophy
of mathematics.
Therein lay their appeal to Borges, and that is why Russell, not Kasner and
Newman, remained Borges' inspiration and touchstone of mathematical thought.
I'll close
the book with a last opening: Borges' solitary annotation on the end leaf of
Kesten's
Copernicus and his World.
There Borges inscribed a Latin phrase
from Copernicus's
De revolutionibus orbium coelestium
and referenced the
page containing the English translation.
Mathemata
mathematicis scribuntur.
"On mathematics,
you write for mathematicians only."
It is my hope that this book
belies that sentiment.
Dissecting
the 3-Sphere
We sail within a vast
sphere, ever drifting in uncertainty, driven from end to end. When we think to
attach ourselves to any point and to fasten to it, it wavers and leaves us; and
if we follow it, it eludes our grasp, slips past us, and vanishes for ever.
Nothing stays for us.
—Blaise
Pascal,
Pensées
The aim here is to see that
three-dimensional slices of a 3-sphere are, in fact, either points or
2-spheres. (We employed this notion in our discussion in the chapter
"Topology and Cosmology" when we relied on lower-dimensional
analogues to yield insight into the nature of the 3-sphere.) For those whose
are interested in this kind of inquiry but whose memory of the equations of
spheres and circles is confined to a misty past, we recommend first reading the
second section of this appendix, which carefully uses the Pythagorean theorem
and the notion of distance in Euclidean space to derive the analytic equations
for a circle, 2-sphere, and 3-sphere.
A way to
understand three-dimensional slices is to use the analytic equation that
defines the unit 3-sphere,
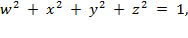
which should be understood as
"the set of all points
(
w, x, y, z
) in coordinatized
four-dimensional space that satisfy the above equation." For example the
point (1, 0, 0, 0) satisfies the equation, as do the points (0, 1, 0, 0) and
(1/2, 1/2, 1/2, 1/2). For the latter point, note that
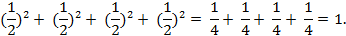
If we fix
w
, the
coordinate for the fourth dimension, at 0, the equation becomes
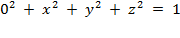 ;
;
