The Unimaginable Mathematics of Borges' Library of Babel (39 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Again, because the second leg
of the dark gray triangle is the hypotenuse of the light gray triangle in
(essentially) the
x
-
y
plane, the Pythagorean theorem allows us to
replace "distance from origin to (
x
,
y
, 0)" with "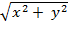 ." We also may think of "height
." We also may think of "height
z
" as just
"
z
," and making these substitutions transforms the previous
equation into
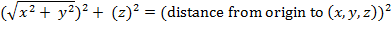
Squaring the square root in
the first term of the above equation and dropping the parentheses leaves us
with

Taking the square root of both
sides of the equation yields
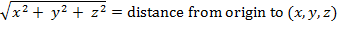
One may now analytically
define the unit 2-sphere in the same way the circle was defined; it is the set
of points (
x
,
y
,
z
) contained in 3-space that all are of
distance one from the origin. This translates into the fact that the 2-sphere
is the set of all points (
x
,
y
,
z
) that satisfy the
distance equation
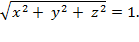
And thus, by squaring both
sides, we arrive at the analytic equation for the 2-sphere:
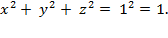
Generalizing these ideas to
coordinatized four-dimensional Euclidean space is similar—we need only adapt
our notion of distance to 4-space. We do this by again bootstrapping ourselves
into a higher dimension by cleverly using Pythagoras twice.
Let
p
= (
w
,
x, y, z
) be a point in 4-space—and notice this time that
the "new" coordinate is added in front of, rather than behind, the
previous coordinates. Once again, the point
p
naturally determines a
right triangle in 4-space (which unfortunately we are unable to draw) with the
first leg of the triangle being the line segment connecting the origin to the
point (0, x, y, z), and this segment is completely contained in the x-y-z
Euclidean 3-space for which the
w
coordinate is constantly equal to 0.
The second leg of the triangle is the line segment "vertically"
connecting (
w
,
x
,
y
,
z
) to (0,
x
,
y
,
z
);
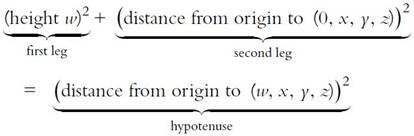
in other words, a leg of "height" equal to
w
. The hypotenuse
of the triangle connects the origin of 4-space to the point
p
, and is
the distance we want. So applying Pythagoras to the right triangle yields
The distance formula in three
dimensions derived earlier allows us to replace "distance from origin to
(0,
x
,
y
,
z
)" with “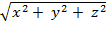 ," and "height
," and "height
w
" is simply equal to "
w
."
Making these substitutions transforms the equation into:

Again, squaring the square
root in the first term of the above equation and dropping the parentheses
leaves us with
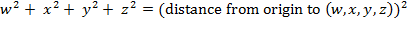
Taking the square root of both
sides yields

