Warped Passages (10 page)

Branes as Slices
In Chapter 1 we looked at one way of thinking about the two-dimensional world of Flatland: as a two-dimensional slice of a three-dimensional space. In Abbott’s novel, the character A. Square took a journey beyond two-dimensional Flatland, into the third dimension, and recognized that Flatland was a mere slice of the bigger three-dimensional world.
Upon his return, A. Square suggested—logically enough—that the three-dimensional world he had seen might also be a mere slice: a three-dimensional slice of an even higher-dimensional space. By “slice,” of course, I don’t mean merely a paper-thin, two-dimensional membrane, but the logical extension of such a thing—a generalized
membrane, if you like. You might think of the three-dimensional slices that A. Square suggested as three-dimensional chunks in four-dimensional space.
But his three-dimensional guide promptly dismissed A. Square’s speculation about three-dimensional slices. Like almost everyone we know, this unimaginative inhabitant of three dimensions believed in only the three dimensions of space he could see; he couldn’t even contemplate a fourth.
Branes have introduced mathematical notions into physics that are similar to those described in
Flatland
over a century ago. Physicists have now returned to the idea that the three-dimensional world that surrounds us could be a three-dimensional slice of a higher-dimensional world. A brane is a distinct region of spacetime that extends through only a (possibly multidimensional) slice of space. The word “membrane” motivated the choice of the word “brane” because membranes, like branes, are layers that either surround or run through a substance. Some branes are “slices” inside the space, but others are “slices” that bound space, like slices of bread in a sandwich.
Either way, a brane is a domain that has fewer dimensions than the full higher-dimensional space that surrounds or borders it.
5
Note that membranes have two dimensions, but branes can have any number of dimensions. Although the branes that will most interest us have three spatial dimensions, the word “brane” refers to all “slices” of this sort; some branes have three spatial dimensions, but other branes have more (or fewer).
6
We’ll use
3-branes
to refer to branes with three dimensions,
4-branes
to refer to those with four, and so on.
Boundary Branes and Embedded Branes
In the previous chapter I explained why we might not see extra dimensions. They could be curled up into sizes so small that evidence of their existence never would appear. The key point was that the extra dimensions would be small. None of the reasons for the invisibility of dimensions relied on the fact that extra dimensions were curled up.
This suggests an alternative possibility: perhaps dimensions are not rolled up, but simply terminate within a finite distance. Because
dimensions that disappear into nothing are potentially dangerous—you wouldn’t want pieces of the universe to fall off the ends—there must be boundaries for the finite dimensions that tell them where and how to end. The question is, what happens to particles and energy when they reach these boundaries?
The answer is that they encounter a brane. In a higher-dimensional world, branes would be the boundaries of the full higher-dimensional space, known as the
bulk
. Unlike a brane, the bulk extends in all directions. The bulk spans every dimension, both on and off the brane (see Figure 25). The bulk is therefore “bulky,” whereas, in comparison, the brane is flat (in some dimensions), like a pancake. If branes bordered the bulk in certain directions, some of the bulk’s dimensions would be parallel to the brane, while other dimensions would lead off it. If the brane is the boundary, the dimensions off the brane would extend only to one side.
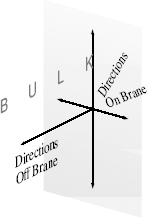
Figure 25.
A brane is a lower-dimensional surface with directions along it and directions that lead away from it, into the higher-dimensional bulk.
To understand the nature of finite dimensions that end on branes, let us consider a very long thin pipe. Within the pipe there are three dimensions: one long and two short. To make the analogy to flat branes most straightforward, let’s imagine that our pipe has a square cross-section. An infinitely long pipe of this type would have four infinitely long straight walls. If the pipe were a universe in its own
right, it would be one with three dimensions, two of which are bounded on either side by walls and one that extends infinitely far.
We know that a long thin pipe when viewed from afar (or with insufficient resolution) looks one-dimensional, much like the garden hose of the previous chapter. But we can also ask, as we did before with the garden-hose universe, how the pipe universe—consisting of the pipe and its interior—would appear to a conscious being living inside.
As you might suspect, this would depend on the being’s resolution. A small fly that could move around within the square pipe would experience it as three-dimensional. Unlike the two-dimensional garden-hose example, we are assuming that the fly can move inside the pipe, and not just on its exterior. Nonetheless, as with the garden hose, the fly would experience the one long dimension differently than the other two. In one direction the fly could go arbitrarily far (assuming that our pipe is very long or infinite), whereas in the other two directions the fly could only go a short distance—the width of the pipe.
But there is a difference between the garden-hose universe and the pipe universe, aside from the number of dimensions each has. Unlike the bug of the previous chapter, the fly in the pipe travels inside it. Thus the fly sometimes encounters walls. It can go back and forth, or up and down, and reach a boundary. The bug on the hose, on the other hand, would never reach such a boundary: instead, it would only go round and round.
When the fly reaches the boundary of its pipe universe, there have to be rules that govern how it behaves. The walls of the pipe determine that behavior. The fly might hit the wall and splat into it; or the pipe might be reflective, so that the fly bounces off. If the pipe were a true universe bounded by branes, then the branes, which would be two-dimensional, would determine what happens when a particle, or anything else that could carry energy, reaches them.
When things get to a boundary brane, they bounce back, just as billiard balls bounce from the edges of the table or light bounces back from a mirror. This is an example of what physicists call a
reflective boundary condition
. If things bounce back from a brane, energy is not lost; it doesn’t get absorbed in the branes or leak away. Nothing goes beyond the branes. The boundary branes are the “ends of the world.”
In a multidimensional universe, branes serve the role of the boundary walls in the pipe-universe example above. Like walls, such branes would have lower dimension than the full space; a boundary always has a lower dimension than the object it bounds. That is as true for the boundary of space as it is for the crust that is the boundary of a loaf of bread. It is also true for the walls in your house, which have one lower dimension than the room they enclose: the room is three-dimensional, whereas any individual wall (when we ignore its thickness) spans only two dimensions.
Although so far in this section I have concentrated on branes that sit at boundaries, branes don’t always sit at the edge of the bulk. They could conceivably exist anywhere in space. In particular, branes might sit somewhere away from the boundary, inside of space. If a boundary brane is like a thin heel at the end of a loaf of bread, such a non-boundary brane would be like a thin slice of bread within the loaf. A non-boundary brane would still be a lower-dimensional object, like the ones we have already considered. But non-boundary branes would have higher-dimensional bulk space on either side.
In the next section, we’ll see that whatever the number of dimensions of the bulk or of the brane, and no matter whether branes are inside a space or at a boundary, branes can trap particles and forces along them. This makes the region of space they occupy very special.
Trapped on Branes
It is very unlikely that you will explore all the space available to you. There are probably places that you wish you had visited and voyages you’ll never take—into outer space or the depths of the sea, for example. You haven’t been to these places, but, in principle, you could go. There is no physical law that makes it impossible.
If, however, you lived inside a black hole, your travel opportunities would be far more severely constrained, more restricted even than those of women in Saudi Arabia. The black hole (until it decayed away) would keep you (or rather, the mutilated, black hole version of you) trapped in the interior, and you would never be able to escape.
There are many more familiar examples of things with restricted
freedom of movement for which there are regions of space that are truly inaccessible. A charge on a wire and a bead on an abacus are both objects that live in a three-dimensional world, but travel in only one of its dimensions. There are also commonplace things that are confined to two-dimensional surfaces. Water droplets on a shower curtain travel only along the curtain’s two-dimensional surface (see Figure 26). Bacteria trapped between microscope slides also experience only two-dimensional motion. Another example is Sam Loyd’s “fifteen” game, the annoying game consisting of a little plastic tray with letters on tiles that you push around until they are correctly arranged in a square and say something like
LOOK
/
YOUF
/
INIS
/
HED
(see Figure 27). Unless you cheat, the letters stay within their plastic enclosure; they can never move in a third dimension.
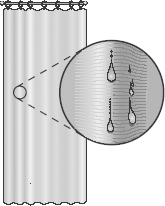
Figure 26.
Drops of water stuck on a two-dimensional shower curtain in a three-dimensional room.
Branes, like shower curtains and Loyd’s fifteen game, trap things on lower-dimensional surfaces. They introduce the possibility that in a world with additional dimensions, not all matter is free to travel everywhere. Just as the water droplets on the curtain are bound to a two-dimensional surface, particles or strings can be confined to a three-dimensional brane sitting inside a higher-dimensional world. But unlike the droplets on the curtain, they are truly trapped. And
unlike the fifteen game, branes are not arbitrary. They are natural players in a higher-dimensional world.

Figure 27.
Sam Loyd’s “fifteen” game.
Particles confined to branes are truly trapped on those branes by physical laws. Brane-bound objects never venture into the extra dimensions that extend off the brane. Not all particles will be trapped on branes; some particles might be free to travel throughout the bulk. But what distinguishes theories with branes from multidimensional theories without them are the particles on the branes—the ones that don’t travel through all the dimensions.
In principle, branes and the bulk could have any number of dimensions, so long as a brane never has more dimensions than the bulk. The
dimensionality of a brane
is the number of dimensions in which brane-confined particles are permitted to travel. Although there are many possibilities, the branes that will be most interesting to us later on will be the three-dimensional ones. We don’t know why three dimensions should appear to be so special. But branes with three spatial dimensions could be relevant to our world because they could extend along the three spatial dimensions we know. Such branes could appear in a bulk space with any number of dimensions that is more than three—four, five, or more dimensions.
