Warped Passages (9 page)

Let’s now apply this reasoning to gravity, and derive the precise distance dependence of the gravitational force in three dimensions. Newton’s gravitational force law follows from two facts: that gravity acts equally in all directions, and that there are three dimensions of space. Let’s now imagine a planet, which attracts any mass in its vicinity. Because the gravitational force is the same in all directions, the strength of the gravitational attraction that the planet exerts on another massive object—a moon, for example—will depend not on direction, but on the distance between them.
To pictorially represent the strength of the gravitational force, the left of Figure 22 shows radial lines extending outwards from the planet’s center, resembling water spreading out from a sprinkler. The density of these lines determines the strength of gravitational attraction that the planet exerts on anything in its vicinity. More force
lines passing through an object would mean a greater gravitational attraction, and fewer force lines would mean a smaller gravitational attraction.

Figure 22.
Gravitational force lines emitted from a massive object, such as a planet. The same number of lines intersect a sphere of any radius; therefore, the force lines are more diffuse and gravity is weaker the farther you are from the massive object at the center.
Notice that the same number of force lines intersect a spherical shell drawn any distance away, no matter how far or near (center and right of Figure 22). The number of force lines never changes. But because the force lines are spread out among all the points on the sphere’s surface, the force at a greater distance is necessarily weaker. The precise dilution factor is determined by the quantitative measure of how widely distributed the force lines are at any given distance.
A fixed number of force lines passes through a sphere’s surface, whatever its distance from the mass. The area of that sphere’s surface is proportional to its radius squared: the surface area is equal to a number multiplied by the square of the radius. Because the fixed number of gravitational force lines is spread out over the sphere’s surface, the gravitational force has to decrease as the square of the radius. This spreading out of the gravitational field is the origin of the inverse square law for gravity.
Newton’s Law with Compact Dimensions
So we now know that in three dimensions, gravity should obey an inverse square law. Notice that the argument seems to depend critically on the fact that there are three spatial dimensions. Had there been only two dimensions, gravity would have been spread out only over a circle, and the force of gravity would have decreased with distance at a slower rate. Had there been more than three dimensions, the surface area of a hypersphere would have grown far more rapidly with the separation between the planet and its moon, and the force would have fallen off that much more quickly. It seems that only three spatial dimensions yields the inverse square distance dependence. But if that is the case, how can theories with extra dimensions yield Newton’s inverse square law for gravity?
It is very interesting to see how compactified dimensions resolve this potential conflict. The essence of the logic is that force lines cannot spread arbitrarily far into the compact dimensions because those com
pact dimensions have finite size. Although force lines initially spread out in all dimensions, when they have spread beyond the extra dimensions’ sizes they have no choice but to spread out solely in the directions of the infinite dimensions.
This can be illustrated once again with our hose example. Imagine that water enters the hose through a small pinhole in a cap covering the end of the hose (see Figure 23). Water directed through the puncture will not immediately travel directly down the hose, but will first spread throughout the tube’s cross-section. Nonetheless, it should be clear that if you were at the other end of the hose, watering your flower, the way the water entered would make no difference at all. Although the water would first spread in more than one direction, it would quickly reach the inside surface of the hose and flow once again as if there were only one direction. This is essentially what happens to gravitational field lines in small, compactified dimensions.

Figure 23.
Water entering a garden hose through a pinhole at the end first spreads in three dimensions before traveling only along the single long dimension of the hose.
As before, we can imagine a fixed number of force lines emanating from a massive sphere. At a distance smaller than the extra dimensions’ size, these force lines will spread out equally in all directions. If you could measure gravity on that small scale, you would measure the consequences of higher-dimensional gravity. The force lines would spread the way water does as it enters the hose through the pinhole and spreads throughout the hose’s interior.
However, at distances greater than the extra dimensions’ sizes, the force lines can spread only in the infinite directions (see Figure 24). In the small, compact dimensions, the force lines will hit the edge of space, so they can’t spread out any farther that way. They have to bend, and the only way for them to go is in the direction of the large
dimensions. Therefore, at distances greater than the sizes of the extra dimensions, it’s just as if the extra dimensions didn’t exist, and the force law reverts to Newton’s inverse square law—the one we observe. This means that even from a quantitative point of view, you won’t know there are extra dimensions if you measure the gravitational force only between objects with separations greater than the curled-up dimensions’ size. The distance dependence reflects extra dimensions only in the tiny region inside the compact space.
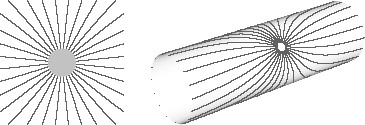
Figure 24.
Gravitational force lines emitted from a massive object when a dimension is curled up. The force lines spread radially over short distances, but over long distances they extend only along the infinite dimension.
Other Ways to Bound Dimensions?
We’ve now established that when extra dimensions are sufficiently small, they are invisible and have no detectable consequences on the length scales we observe. For a long time, string theorists assumed that extra dimensions were Planck-length dimensions, but recently some of us have questioned this assumption.
No one understands string theory well enough to say definitively what the sizes of extra dimensions will turn out to be. Sizes comparable to the Planck length are possible, but any dimension too small to observe is also in the running. The Planck length is so tiny that even considerably larger curled-up dimensions might well escape notice. An important question for the study of extra dimensions is just how big these dimensions can be, given that we haven’t seen them yet.
The questions we’ll address in this book include how big extra
dimensions can be, whether these dimensions have any discernible effect on elementary particles, and how experiments might probe them. We will see that the existence of extra dimensions can significantly change the rules by which we do particle physics and, furthermore, that some of these changes will have experimentally observable consequences.
An even more radical question we’ll investigate is whether additional dimensions have to be small. We don’t see tiny dimensions, but do dimensions have to be small to be invisible? Could an extra dimension possibly extend for ever without our seeing it? If so, extra dimensions would have to be very different from the dimensions we’ve looked at. So far I’ve presented only the simplest possibility. We’ll see later why even the radical possibility of an infinite extra dimension cannot be excluded if it is sufficiently different from the three familiar infinite dimensions.
The next chapter will address yet another question that might have occurred to you: why can’t small extra dimensions just be intervals, not curled up into a ball but instead bounded between two “walls”? This possibility didn’t occur to anyone right away—but why not? The reason is that imagining an end to space entails knowing what is happening there. Would things fall off the end of the universe, as old pictures of the flat Earth seemed to imply? Or would they be reflected back? Or would they never get there? The need to specify what would happen at the end means that you have to know what scientists call
boundary conditions
. If space ends, where and on what does it end?
Branes—membrane-like objects in higher-dimensional space—provide the necessary boundary conditions for worlds that “end.” As we will see in the following chapter, branes can make a world (or many worlds) of difference.
Exclusive Passages: Branes, Braneworlds, and the Bulk
I’m gonna stick like glue,
Stick, because I’m stuck on you.
Elvis Presley
Unlike the studious Athena, Ike rarely read any books. He generally preferred playing with games, gadgets, and cars. But Ike hated driving in Boston, where the drivers were reckless, the roads were badly signposted, and the highways were invariably under construction. Ike always ended up stuck in traffic, which he found especially frustrating when he could see a nearly empty freeway overhead. Though the empty road would be tempting, Ike would have no way to quickly reach it since, unlike Athena’s owls, he couldn’t fly. For Ike trapped on slow roads in Boston, the third dimension was no use at all.
Until very recently, few self-respecting physicists considered extra dimensions worth thinking about. They were too speculative and too foreign: no one could say anything definitive about them. But in the last few years, extra dimensions have found their fortunes rising. No longer shunned as undesirable gatecrashers, they’ve evolved into highly sought-after, stimulating company. They owe their newfound respectability to branes and to the many genuinely new theoretical possibilities that these fascinating constructs have introduced.
Branes took the physics community by storm in 1995, when the physicist Joe Polchinski of the Kavli Institute for Theoretical Physics
(KITP) in Santa Barbara established that they were essential to string theory. But even before then, physicists had proposed branelike objects. One such example was a
p-brane
(so called by p-layful p-hysicists), an object that extends infinitely far in only some dimensions, which physicists derived mathematically using Einstein’s theory of general relativity. Particle physics had also suggested mechanisms for confining particles on branelike surfaces. But string theory branes were the first known type of brane that could trap forces as well as particles, and we’ll soon see that is part of what makes them so interesting. Like Ike stuck on a two-dimensional road in three-dimensional space, particles and forces can be trapped on lower-dimensional surfaces called branes, even if the universe has many other dimensions to explore. If string theory accurately describes the world in which we live, physicists have no choice but to acknowledge the potential existence of such branes.
The world of branes is an exciting new landscape that has revolutionized our understanding of gravity, particle physics, and cosmology. Branes might really exist in the cosmos, and there is no good reason that we couldn’t be living on one. Branes might even play an important role in determining the physical properties of our universe and ultimately explain observable phenomena. If they do, branes and extra dimensions will be here to stay.
