Warped Passages (17 page)

Gravitational mass, on the other hand, is the mass that enters the gravitational force law and determines the strength of gravitational attraction. As we saw, the strength of the Newtonian gravitational force is proportional to the two masses that get attracted to each other. These masses are gravitational mass. Gravitational mass and the inertial mass that enters Newton’s second force law turn out to be the same, and that’s why we can safely give them the same name: mass. But in principle they could have been different, and we would have had to call one “mass” and the other “ssam.” Fortunately, we don’t need to do that.
The mysterious fact that the two masses are the same has deep implications, which it took an Einstein to recognize and develop. The gravitational force law states that the strength of gravity is proportional to mass, and Newton’s law tells us how much acceleration would be generated by that (or any other) force. Because the strength of gravity is proportional to the same mass that determines the amount
of acceleration, the two laws together tell us that even though the
force
depends on mass through
F
=
ma
, the acceleration induced by gravity is entirely independent of the mass that gets accelerated.
The acceleration of gravity that any object experiences must be the same for anyone or anything separated by the same distance from another object. This is the claim that Galileo allegedly verified by dropping objects off the Tower of Pisa,
*
demonstrating that the Earth induces the same acceleration for all objects, independent of their mass. This fact—that acceleration is independent of the mass of the accelerated object—is unique to the gravitational force, because the strength of no force other than gravity depends on mass. And because the gravitational force law and Newton’s law of motion depend on mass in the same way, the mass cancels out when you calculate acceleration. Acceleration therefore doesn’t depend on mass.
This relatively straightforward deduction has profound implications. Since all objects have the same acceleration in a uniform gravitational field, if this
single
acceleration could be canceled, the evidence of gravity would be canceled as well. And that is exactly what happens to a freely falling body: it is accelerated precisely so as to cancel the evidence of gravity.
The equivalence principle says that if you and everything around you were freely falling, you would not be aware of a gravitational field. Your acceleration would cancel the acceleration that the gravitational field would otherwise have produced. This state of weightlessness is now familiar from pictures from orbiting spacecraft, where the astronauts and the objects that surround them don’t experience any gravity.
Textbooks often illustrate the absence of gravity’s effects (from the vantage point of the freely falling observer) with a picture of someone dropping a ball in a free-falling elevator. You see the person and the ball falling together in the picture. The person in the elevator would always see the ball at the same height above the elevator’s floor. He wouldn’t see the ball drop (see Figure 36).
Physics texts always present the freely falling elevator as if it were the most natural thing in the world that the observer inside would
calmly watch a ball not drop with complete equanimity, with no concern at all for his personal well-being. This is in sharp contrast to the terrified faces in movies in which the cables of an elevator are cut and the actors hurtle towards the ground. Why such different responses? If everything were freely falling, there would be no cause for alarm. The situation would be indistinguishable from everything being at rest, albeit in a zero-gravity environment. But if, as in the movies, someone is falling but the ground below him stays put, he has good reason to be petrified. If someone is on a freely falling elevator, but solid ground awaits his descent, you can be sure that he will notice the consequences of gravity when his free fall is ended (as is illustrated in the last frame of Figure 36).
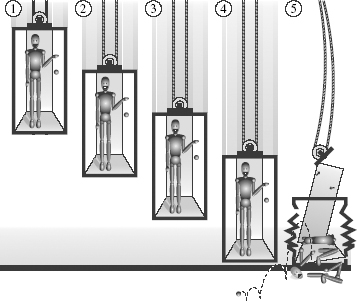
Figure 36.
An observer in a falling elevator who releases a ball will not see it drop. However, when a freely falling elevator meets the stationary Earth, the observer will not be very happy.
The reason that Einstein’s conclusion seems so surprising and strange is that our upbringing here on Earth, with a stationary planet beneath our feet, biases our intuition. When the force of the Earth keeps you stationary on the ground, you notice the effects of gravity because you are not following the path towards the center of the Earth
that gravity would have you follow. On Earth, we’re accustomed to gravity making things fall. But “falling” really means “falling relative to us.” If we were falling along with a dropped ball, as we would be in a free-falling elevator, the ball would not go down any faster than we would. We therefore would not see it drop.
In your freely falling reference frame, all the laws of physics would coincide with the laws of physics that would be obeyed if you and everything near you were at rest. A freely falling observer would observe that motion is described by the same equations, consistent with special relativity, that apply for observer in an inertial, non-accelerating reference frame. In the review paper he wrote in 1907 about relativity, Einstein explains how the gravitational field has only a relative existence, “because for an observer falling freely from the roof of a house there exists—at least in his immediate surroundings—no gravitational field.”
*
This was Einstein’s major insight. The equations of motion for a freely falling observer are the equations of motion for an observer in an inertial reference frame. A freely falling observer does not feel the force of gravity—only objects that are not in free fall experience a gravitational force.
In our lives we don’t generally encounter things or people in free fall. When free fall happens, it looks scary and dangerous. But, as an Irishman said to the physicist Raphael Bousso when he was visiting Ireland’s Cliffs of Moher, “It’s not the fall that kills you, but the %&!# crash when you stop.” And when I broke several bones in a rock-climbing accident and had to miss a conference I had organized, there were quite a few jokes about my testing the theory of gravity. I can state with complete confidence that gravitational acceleration agrees with predictions.
Tests of General Relativity
There’s more to general relativity; soon we’ll get to the rest, which took considerably longer to develop. But the equivalence principle alone explains many results from general relativity. Once Einstein had recognized that gravity could be canceled in an accelerating reference frame, he could calculate gravitational influence by imagining an accelerating system equivalent to the one with gravity. This allowed him to calculate the gravitational effects for some interesting systems which others could use to check his conclusions. We’ll now consider a few of the most significant experimental tests.
First is the
gravitational redshift
of light. A redshift causes us to detect light waves at a lower frequency than the frequency at which they were emitted. (You’ve probably encountered the analogous effect in sounds waves when a motorcycle roared past you and the sound waves rose and fell in pitch.)
There are several ways to understand the origin of the gravitational redshift, but probably the simplest is through an analogy. Imagine that you throw a ball up into the air. The rising ball slows down as it moves against the force of gravity. But the ball’s energy is not lost, even though the ball is slowing down. It is converted into potential energy, which is then released as kinetic energy, or energy of motion, when the ball falls back down.
The same reasoning applies to the particle of light, the
photon
. Just as a ball loses momentum when it is thrown up into the air, a photon loses momentum as it escapes from a gravitational field. As with the ball, this means that the photon loses kinetic energy but gains potential energy as it fights its way out of the gravitational field. But a photon cannot slow down as a ball would, since it always travels at the constant speed of light. To jump the gun a bit, we will see in the next chapter that one consequence of quantum mechanics is that a photon lowers its energy when it lowers its frequency. And that is exactly what happens to the photon that is going through the changing gravitational potential. In order to lower its energy, the photon decreases its frequency, and this lowered frequency is the gravitational redshift.
Conversely, a photon that was moving towards a gravitational source would increase its frequency. In 1965, the Canadian-born physicist Robert Pound and one of his students, Glen Rebka, measured this effect by studying gamma rays emitted from radioactive iron that was placed at the top of the “tower” of Harvard’s Jefferson Lab, the building where I now work. (Though it’s part of the building, an elevated attic area in Jefferson Lab and the floors beneath it are known as “the tower.”). The gravitational fields at the top and bottom of the tower were slightly different, since the top is slightly further from the center of the Earth. A high tower would be best for this measurement, since it would maximize the difference in height between where the gamma rays were emitted (the top of the tower) and where they were detected (the basement). But even though the tower consists of just three floors, an attic, and some windows that peer out above the attic—it’s all of 74 feet high—Pound and Rebka managed to measure the difference in frequency between the emitted and absorbed photons with incredible precision, five parts in a million billion. They thereby established that the general relativity predictions for the gravitational redshift were correct to at least 1% accuracy.
A second experimentally observable consequence of the equivalence principle is the bending of light. Gravity can attract energy as well as mass. After all, the famous relation
E
=
mc
2
means that energy and mass are closely connected. If mass experiences gravity, then so should energy. The Sun’s gravity influences mass, and likewise affects the trajectory of light. Einstein’s theory predicted exactly the amount light should bend under the Sun’s influence. These predictions were first confirmed during the solar eclipse of 1919.
The English scientist Arthur Eddington organized expeditions to the island of Principe off the coast of West Africa and to Sobral in Brazil, where the eclipse could best be seen. Their purpose was to photograph the stars in the neighborhood of the eclipsed Sun and check whether stars that appeared near the Sun moved relative to their usual positions. If the stars did appear to be shifted, that would mean that their light was traveling along a bent trajectory. (The scientists needed to make their measurements during an eclipse so that the sunlight wouldn’t overwhelm the much dimmer light of the stars.) Sure enough, the stars appeared in just the right “wrong” places. The
measurement of the correct bending angle provided strong evidence supporting Einstein’s theory of general relativity.
Incredibly, the bending of light is now so well established and understood that it is one of the tools that was used to probe the distribution of mass in the universe and look for dark matter in the form of small, burnt-out stars that no longer emit light. Like black cats on a moonless night, such objects are very hard to see. The only way to observe them is through their gravitational effects.
Gravitational lensing is one way that astronomers can learn about dark objects; dark objects, like everything else, interact via gravity. Although the burnt-out stars do not themselves emit light, there can be bright objects behind them (from our perspective) whose light we can see. Without any dark star near its path, the light would travel in straight lines. But light emitted by a bright star will bend when it passes by the dark star. Light passing on the left will bend in the opposite direction than light passing on the right and light passing on the top will bend in the opposite direction than light passing on the bottom. This will create multiple images of a bright object behind a dark star and the effect is called
gravitational lensing
. Figure 37 shows an example of a multiple image of a star that appeared when an intervening massive object bent the star’s light rays in different directions.
The Graceful Curves of the Universe
The equivalence principle says that the force of gravity is indistinguishable from constant acceleration. I’m glad you made it to this point, because I need to confess that I simplified, and the two aren’t entirely indistinguishable after all. How could they be? If gravity were equivalent to acceleration, it would not be possible for people in opposite hemispheres to simultaneously fall to Earth. After all, the Earth cannot accelerate in two directions at once. Gravitational pull in the different directions felt in America and China, for example, cannot possibly be accounted for by a single acceleration.
