Warped Passages (42 page)

The properties of these particles and their superpartners are rigidly aligned to one another: the bosonic superpartners have the same masses and charges as their fermionic counterparts, and they also have related interactions. For example, if the electron has charge -1, so does the selectron; and if a neutrino interacts via the weak force, so does the sneutrino.

If the universe is supersymmetric, bosons must also have superpartners. The known bosons in the Standard Model are the force carriers: the photon, the charged Ws, the Z, and the gluons, all of which have spin-1. The nomenclature of supersymmetry dictates that the new fermionic superpartners have the same name as the boson with which they are paired with “-ino” tacked on at the end. So the fermionic partners of gauge particles are called
gaugino
particles, the fermionic partners of gluons are
gluinos
, and the fermionic partner of the Higgs particle is a
Higgsino
. As was true for bosonic superpartners, fermionic superpartners have the same charges, the same interactions, and—if supersymmetry is exact—the same mass as the boson with which they are paired (see Figure 64).

You might find it remarkable that physicists take the possibility of supersymmetry as seriously as they do, given that no superpartner has ever been found. I’m sometimes surprised how confident some of my colleagues are about it. But even though supersymmetry has not yet been found in nature, there are several reasons to suspect its presence.
Sergio Ferrara, one of the first to work on supersymmetry, expressed the view of many physicists when he told me on our train ride to London that it would be hard to believe that such a surprising and fascinating theoretical construction played no role in the physics of the world.

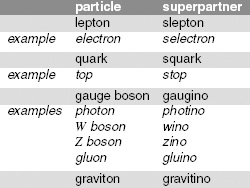
Figure 64.
Particles and their supersymmetric partners.

Other physicists, less taken with the beauty of the symmetry, believe in supersymmetry primarily because of the benefits of the supersymmetric extensions of the Standard Model. Unlike non-supersymmetric theories, they protect the light Higgs particle and the hierarchy of masses.

Supersymmetry and the Hierarchy Problem

The hierarchy problem in the Standard Model was the question of why the Higgs particle is so light. How can there be a light Higgs particle when there are large quantum contributions to its mass from virtual particles? These large contributions tell us that the Standard Model works only if it contains an enormous and unfortunate fudge.

The big advantage of a supersymmetric extension of the Standard Model is that when there are virtual contributions from both particles and superpartners, supersymmetry guarantees the absence of the large quantum contributions to the Higgs particle’s mass that made a light Higgs particle seem so unlikely. Supersymmetric theories can have
are correlated. And because of the constraints this imposes, supersymmetric theories don’t have problems with large quantum contributions to particle masses.

In a supersymmetric theory, the virtual Standard Model particles aren’t the only virtual particles that contribute to the Higgs particle’s mass. Virtual superpartners do, too. And because of the remarkable properties of supersymmetry, the two kinds of contribution always add up to zero. The quantum contributions of virtual fermions and bosons to the Higgs particle’s mass are related so precisely that the large contributions made by either bosons or fermions individually are guaranteed to cancel each other out. The value of the fermions’ contribution is negative and exactly cancels the bosons’ contribution.

One such cancellation is illustrated in Figure 65, which shows two diagrams, one with a virtual top quark, and one with a virtual stop squark. Each of the individual diagrams would lead to a large contribution to the Higgs particle’s mass. But because of the special relationships between particles and interactions in supersymmetric theories, the huge quantum contributions to the mass from the top quarks and the stop squarks are obliterated because they add up to zero.

Figure 65.
In a supersymmetry theory, the Higgs particle’s mass gets contributions from both particles and supersymmetry particles (in this case, a virtual top quark and virtual antitop quark in one diagram, and a virtual stop quark and virtual antitop quark in the other). The two diagrams look different because the interactions of the fermions and bosons are different. Nonetheless, the contributions to the Higgs particle’s mass from the two diagrams cancel when added together.

In a non-supersymmetric theory, huge quantum contributions to the mass of the Higgs particle would destroy low-energy electroweak symmetry breaking unless a huge and unlikely fudge made all the
large contributions to the particle’s mass add up to a very small number. But a supersymmetric extension of the Standard Model guarantees that any potentially destabilizing influences, such as the ones shown in these diagrams, will add up to zero. A small value for the classical mass of the Higgs particle guarantees that the true mass—which includes the quantum contributions—will also be small.

Supersymmetry is like a flexible, stable foundation for the Standard Model. If you imagine the Standard Model’s fine-tuning as the balancing required to make a pencil stand on end then supersymmetry is like a fine wire holding the pencil in place. Alternatively, if you think of the hierarchy problem as the INS officers overstepping their jurisdiction and delaying too many letters, supersymmetric partners are like civil liberty advocates who restrain the immigration officers and let most of the letters pass right through.

Because ordinary virtual particles’ contributions together with the supersymmetric partners’ contributions add up to zero, supersymmetry guarantees that quantum mechanical contributions from virtual particles do not eliminate low-mass particles from the theory. In a supersymmetric theory, a particle that is supposed to be light, such as the Higgs particle, will remain light, even when we take virtual contributions into account.

Broken Supersymmetry

Although supersymmetry potentially resolves the problem of large virtual contributions to the Higgs particle’s mass, there is a serious problem with supersymmetry as I have presented it so far. The world is manifestly not supersymmetric. How could it be? If there existed superpartners with identical masses and charges to those of the known particles, they too would already have been seen. Yet no one has discovered a selectron or a photino.

This doesn’t mean that we have to abandon the idea of supersymmetry. But it does mean that supersymmetry, should it exist in nature, cannot be an exact symmetry. Like the local symmetry that accompanies the electroweak force, supersymmetry must be broken.

Theoretical reasoning shows that supersymmetry can be broken by
particles and their superpartners not having identical masses; small supersymmetry-breaking effects can distinguish them. The difference between a particle’s mass and that of its corresponding superpartner would be controlled by the degree to which supersymmetry is broken. If supersymmetry is broken only a little, the mass difference will be small, whereas if it is badly broken, the difference will be large. In fact, the difference in mass between particles and their superpartners is one way to describe how badly supersymmetry is broken.

In almost all models of supersymmetry breaking, the superpartners’ masses are greater than the masses of the known particles. This is fortunate, since superpartners being heavier than their Standard Model counterparts is critical to the consistency of supersymmetry with experimental observations. It would explain why we haven’t yet seen them. Heavier particles can be produced only at higher energies, and, if supersymmetry exists, colliders have presumably not yet achieved sufficiently high energy to produce them. Because experiments have explored energies up to a few hundred GeV, the fact that superpartners have not yet been seen tells us that if they exist, they must have masses that are at least that big.

The specific mass that a superpartner must exceed to have eluded detection depends on that particular particle’s charge and interactions. Stronger interactions make particles easier to produce. So to avoid being detected, particles with stronger interactions must be heavier than more weakly interacting ones. Current experimental constraints on most models of supersymmetry breaking tell us that, should supersymmetry exist, all superpartners must have a mass of at least a few hundred GeV to have escaped detection. Those superpartners that are subject to the strong force, such as the squarks, must be even heavier—with masses of at least a thousand GeV.

Broken Supersymmetry and the Higgs Particle Mass

As we’ve seen, the quantum contributions to the Higgs particle’s mass are not problematic in supersymmetric theories because supersymmetry guarantees that they add up to zero. However, we have also just seen that supersymmetry must be broken if it is to exist in the
real world. Because superpartners don’t have the same mass as their Standard Model counterparts in a model with broken supersymmetry, the quantum contributions to the Higgs particle’s mass are not so rigidly balanced as they are when supersymmetry is exact. So when supersymmetry is broken, virtual contributions no longer cancel exactly.

Nonetheless, so long as the quantum contributions to the Higgs particle’s mass are not too large, the Standard Model can get by without fine-tuning or fudging. Even when supersymmetry is broken—so long as the effect is small—the Standard Model can contain a light Higgs particle. Supersymmetry, even if broken a little bit, is sufficiently powerful to eliminate the huge Planck scale mass contributions from virtual energetic particles. With only a small amount of supersymmetry breaking, no exceptionally unlikely cancellations would be necessary.

We want supersymmetry breaking to be small enough to make the supersymmetry-breaking mass difference between superpartners and Standard Model particles sufficiently small to avoid fudging. It turns out that the quantum contribution to the Higgs particle’s mass from a virtual particle and its superpartner, though nonzero, will never have a magnitude much greater than the supersymmetry-breaking mass difference between the particle and its superpartner. That tells us that the mass differences between all particles and their superpartners should be about the weak scale mass. In that case the quantum contributions to the Higgs particle’s mass would also be about the weak scale mass, which is about the right size for the mass of the Higgs particle.

Because known particles in the Standard Model are light, the mass difference between a superpartner and a Standard Model particle will be comparable to the superpartner’s mass. Therefore, if supersymmetry solves the hierarchy problem, the superpartner masses should not be much greater than the weak scale of about 250 GeV.

If the superpartner masses are about the same as the weak scale mass, the quantum contribution to the Higgs particle’s mass will not be very large. Unlike the non-supersymmetric case, in which quantum contributions to the Higgs particle’s mass were sixteen orders of magnitude too big, so that intolerable fudging was required to
maintain a light Higgs particle, a supersymmetric world with supersymmetry-breaking masses of a few hundred GeV would generate no excessively large quantum contributions to the Higgs particle’s mass.

The requirement that the Higgs particle, and therefore the superpartners, not be much heavier than a few hundred GeV (so as not to reintroduce large quantum contributions to the Higgs particle’s mass), coupled with the fact that experiments have already looked for superpartners with masses of about a couple of hundred GeV, tells us that if supersymmetry exists in nature and solves the hierarchy problem, then supersymmetric partners must have masses that are about a few hundred GeV. This is quite exciting because it suggests that experimental evidence of supersymmetry could be just around the corner and could appear at particle colliders some time very soon. Only a small increase in energy over the existing collider, the Tevatron, should be sufficient to reach the energies at which superpartners would have to appear.