Warped Passages (45 page)

Strings extend along a single dimension. At any given time, you need only one number to identify a point along a string, so according to our definition of dimensionality, strings are one-(spatial) dimensional objects. Nonetheless, like real, physical pieces of string, they can curl up and loop around. In fact, there are two types of string:
open strings
, which have two endpoints, and
closed strings
, which are loops with no ends (see Figure 67).
Which particles a string actually produces depends on the string’s
energy and on the precise vibrational modes that are excited. Modes of a string are like the resonant modes of a violin string. You can think of the oscillations as elementary units that can be combined to form all known particles. In this language, particles are chords and their interactions are harmonies. The string of string theory doesn’t always produce all particles, just as a violin string doesn’t produce any sound until someone applies a bow. But just as a bow excites the modes of a violin, energy will excite the modes of a string. And when the string has enough energy, it will produce different particle types.

Figure 67.
An open string and a closed string.
For both open and closed strings, the resonant modes are those that oscillate an integer number of times along the string’s length. A few such modes are depicted in Figure 68. For these modes, the wave oscillates up and down some number of times, with all oscillations completed over the length of the string. For an open string, the wave vibrations hit the end of the string and turn around, going back and forth, whereas waves on closed strings oscillate up and down as they
wind around the closed string loop. Any other waves—those that don’t complete an integer number of oscillations—won’t occur.
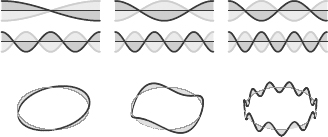
Figure 68.
Some string oscillation modes for (above) an open and (below) a closed string.
Ultimately, the precise way that the string oscillates determines all of a particle’s properties, such as its mass, spin, and charge. In general, there will be many copies of particles with the same spin and charge, all with different masses. Because of the infinite number of such modes, a single string can give rise to an infinite number of heavy particles. Known particles, which are relatively light, arise from strings with the fewest oscillations. A mode with no oscillations could be a familiar light particle, such as an ordinary quark or lepton. But an energetic string can oscillate in many ways, so string theory is distinguished by its heavier particles, which arise from higher vibrational modes.
However, more oscillations require more energy. The extra particles from string theory that arise from more oscillations are likely to be extremely heavy—an enormous amount of energy would be required to produce them. So even if string theory is correct, its novel consequences are likely to be extremely difficult to detect. Since we don’t expect to produce any of the new heavy particles at accessible energies, we expect string theory and particle physics to give rise to the same observable consequences at the energies we see. This picture might change if some of the recent developments about extra dimensions are correct. But for now, let’s review the conventional string theory picture. We’ll catch up with extra-dimensional models later on.
String Theory’s Origins
By the future Ike XLII’s time, string theory could boast quite a long history. But for scientific purposes, we’ll confine our story to the twentieth and early twenty-first centuries. We now think of string theory as a theory that might reconcile quantum mechanics and gravity. Originally, however, it had a completely different application. The theory first emerged in 1968 as an attempt to describe the strongly interacting particles known as the hadrons. That theory was not successful; as we saw in Chapter 7, we now know that hadrons are
made from quarks held together through the strong force. Nonetheless, string theory survived—not as a theory of hadrons, but as a theory of gravity.
Despite its failure to describe hadrons, we can learn a little about the good features of the string theory of gravity by examining a few of the problems that hadronic string theory faced. Remarkably, the failures of the string theory of hadrons were redeeming features (or at least not obstacles) for the string theory of quantum gravity.
The first problem with the original version of string theory was that it contained a
tachyon
. People initially thought of tachyons as particles traveling faster than the speed of light (the term comes from the Greek
tachos
, meaning “speed”). But we now know that a tachyon indicates an instability in a theory that contains it. Regrettably for science fiction fans, tachyons are not real physical particles that appear in nature. If your theory seems to contain a tachyon, you are analyzing it incorrectly. A system that contains a tachyon can (and will) transform itself into a related system with lower energy in which the tachyon is absent. The system with the tachyon doesn’t last long enough for it to have any physical effects; it’s only a feature of the incorrect theoretical description. You need to find a theoretical description of the related stable configuration without a tachyon before you can identify true physical particles and forces. Unless it contains such a configuration, your theory is incomplete.
String theory with a tachyon didn’t seem to make sense. But no one knew how to formulate the theory in a way that eliminated it. This meant that the predictions from string theory, including those for particles other than the tachyon, were not reliable. You might think that this should have been reason enough to abandon hadronic string theory. But physicists held out hope that the tachyon wasn’t real; some thought it might simply be a problem with the mathematical approximations that were made when formulating the theory, but that wasn’t very likely.
However, Ramond, Neveu and Schwarz discovered an alternative supersymmetric version of string: the
superstring
. Superstring theory’s critically important advantage over the original version of string theory was that it contained spin -½ particles, giving it the potential to describe the Standard Model fermions such as the electron and the
different types of quark. But an added bonus of superstring theory was that it did not contain the tachyon that had plagued the original version of string theory. The superstring, which seemed a more promising theory in any case, didn’t have the tachyon instability that would have threatened to hamper its progress.
A second problem for the original string theory of hadrons was that it contained a massless spin-2 particle. Calculations showed that there was no way to eliminate it, but no experimenter had ever discovered this pesky particle. Since experimenters should have been able to observe any massless particle that interacted as strongly as a hadron, hadronic string theory appeared to be in trouble.
Scherk and Schwarz turned string theory on its head when they showed that the “bad” spin-2 particle that confounded hadronic string theory might in fact be the crowning glory of a string theory of gravity; the spin-2 particle could actually be the graviton. They went on to show that the spin-2 particle behaved just as a graviton should. The critical observation that string theory contained a candidate for the graviton made string theory a potential theory of quantum gravity. With a particle description, no one had figured out how to formulate a consistent theory of gravity that worked at all energies. A string theory description, on the other hand, looked like it might do the trick.
There was another indication that although a string theory of hadrons wouldn’t work, Scherk and Schwarz might be on the right track with a string theory of gravity. As we saw in Chapter 7, Friedman, Kendall, and Taylor at the Stanford Linear Accelerator Center (SLAC) showed that electrons dramatically scatter from nuclei, implying the existence of hard, pointlike objects—namely quarks—inside. This experiment was similar in spirit to the Rutherford scattering experiment described in Chapter 6. The dramatic scattering results in that case pointed to a hard atomic nucleus, and in this case to pointlike quarks inside the nucleons—not to fluffy, extended strings.
However, the predictions of string theory did not agree with the SLAC experiment’s results. Strings would never lead to the dramatic scattering that only a hard, compact object could cause. Because only pieces of the strings would interact at any given time, strings would
collide more softly. This quiet, relatively undramatic, scattering was the death knell for the string theory of hadrons. However, from the vantage point of quantum gravity it looked like it could be a very promising property.
In a particle theory of the graviton, the graviton interacts far too strongly at high energies. A better theory would be one in which energetic gravitons don’t interact so fiercely. And that is what happens in a string theory of gravity. String theory, which replaces pointlike particles with extended strings, guarantees that the graviton interacts much less dramatically at high energies. Strings—unlike quarks—have no hard scattering processes. They have more “mushy” interactions that take place over an extended region.
24
This property means that string theory could potentially solve the problem of the graviton’s ridiculously high interaction rate, and correctly predict high-energy graviton interactions. Strings’ softer high-energy collisions were another important indicator that a string theory of gravity might be correct.
In summary, superstring theory contains fermions, force-carrying gauge bosons, and the graviton—all the types of particle we know about. It doesn’t contain a tachyon. Furthermore, superstring theory includes a graviton whose quantum description potentially makes sense at high energies. String theory looked like it could potentially describe all known forces. It was a promising candidate theory of the world.
The Superstring Revolution
Superstring theory was an extremely bold step, even to solve a problem as deep as quantum gravity. A string theory of gravity predicts an infinitely large number of particles beyond those we know. Moreover, string theory is extremely difficult to analyze with computations. What a steep price to pay for solving the problem of quantum gravity: a theory with infinitely many new particles and a potentially intractable mathematical description. Working on string theory in the 1970s required individuals who were either very determined or somewhat
crazy. Scherk and Schwarz were among the very few who negotiated this risky path.
After Scherk’s untimely death in 1980, Schwarz persevered with string theory. He collaborated with another (perhaps the only) convert at that time, the British physicist Michael Green, and together they worked out the consequences of the superstring. Schwarz and Green discovered a bizarre feature of the superstring: it makes sense only in ten dimensions, nine of space and one of time. In any other number of dimensions, unacceptable vibrational modes of the string give rise to manifestly nonsensical predictions, such as negative probabilities for processes involving modes of the string that should not exist. In ten dimensions, all the unwanted modes are eliminated. A string theory in any other number of dimensions made no sense.
To clarify, the string itself extends along a single spatial dimension and travels through time. Those were the two dimensions that Ramond had studied when he first discovered supersymmetry. But just as we know that a pointlike object—which has no extent in any spatial dimensions, and therefore has zero spatial dimensions—can move about in three dimensions of space, a string—which has one spatial dimension—can move around in a space with many more dimensions than it itself possesses. Strings could conceivably move around in three, four, or more dimensions. Calculations indicated that the correct number (including time) was ten.
Having too many dimensions was not a novel feature of the superstring. The earlier version of string theory (the one without fermions or supersymmetry) had twenty-six dimensions: one of time and twenty-five of space. But the earlier version of string theory had other problems, like the tachyon. Superstring theory, on the other hand, was sufficiently promising to be worth pursuing.
