Why Beauty is Truth (22 page)

Why the quintic is unsolvable.

Well, not quite. We could take all sorts of other roots, build a huge, tall tower. But such a tower cannot have a root in its attic unless
some
floor corresponds to the particular square root that I
am thinking about. And none of the previous floors will help you reach the attic; building them was a waste of time and money. So any sensible builder will go for that square root right at the start.

What do you need to climb the ladder to the third floor?

There
is
no ladder to the third floor. You can reach the second floor, but then you are stuck. And if you can't reach the third floor of the presumed tower, you certainly can't get to the attic and find a root in the sack.

In short, the Tower of Abel does not exist. All that exists is an abandoned attempt that peters out on the second floor; or perhaps a more elaborate structure with lots of unnecessary floors, which eventually peters out in exactly the same manner, for exactly the same reason. This is what Ruffini proved, save for one technical gap. Roughly speaking, he failed to prove that if harmless combinations of radicals live in the attic, then so do the radicals themselves.

Ruffini's proof and Abel's towers have clear similarities. But by using towers, Abel improved Ruffini's tactics and filled the gap he left. Between them, they proved that
no
radical tower climbs from the coefficients of the quintic to its roots. In architectural language, that tells us that there is no formula for the root of a quintic that uses nothing more elaborate than radicals. Solving the quintic by radicals is as impossible as climbing to the Moon by repeatedly standing on your own shoulders.

As Christmas 1828 drew near, Abel arranged to stay with his old friends Catharine and Niels Treschow in Froland. He was looking forward to visiting Crelly, who lived nearby. His doctor didn't think the trip was a good idea, because of the state of Abel's health. In a letter to Christoffer Hansteen's wife, Johanne, Catharine wrote, “If only you had been in town he might have been content to remain. But he tried to hide how ill he really was.” In mid-December Abel headed for Froland, bundled up against the winter cold. He arrived on 19 December wearing every scrap of clothing he had with him, including socks over his arms and hands. Despite his coughs and cold shivers, he plowed ahead with his mathematics, happy to work in the Treschows' parlor surrounded by their children. He enjoyed the company.

Abel was still trying to land a permanent position. Even his temporary post at Oslo was in doubt. Over Christmas he focused his main efforts on securing the job in Berlin. His friend August Crelle, busy behind the
scenes, had persuaded the Department of Education to create a mathematical institute and was angling for Abel to be appointed as one of its professors. He had obtained support from the scientific giant Alexander von Humboldt, together with a recommendation from Gauss and another from Adrien-Marie Legendre, a prominent member of the French Academy. Crelle advised the education minister that Abel was willing to accept a position in Berlin, but that the authorities should move quickly because he was in demand elsewhere, notably Copenhagen.

Abel was due to leave Froland for Oslo on 9 January, but his coughs and chills had worsened and he spent most of his time confined to his room. His intended in-laws, the Kemps, became very worried. On the morning of his planned departure he was coughing violently and spitting blood. The family doctor was immediately called to the house, and he prescribed bed rest and constant nursing. Crelly acted as nurse, and her loving attentions and various medications led to a distinct improvement. Within a few weeks Abel was allowed to sit in a chair for short periods. He had to be restrained from doing any mathematics.

Legendre wrote to say how impressed he was with Abel's work on elliptic functions, and urged the young man to publish his solution to the problem of deciding when an equation could be solved by radicals: “I urge you to let this new theory appear in print as quickly as you are able. It will be of great honor to you, and will universally be considered the greatest discovery which remained to be made in mathematics.” While some prominent mathematicians, actively or through neglect, were hindering the publication of Abel's seminal works, his reputation in other quarters was growing fast.

Toward the end of February 1829, Abel's doctor realized that he was never going to recover, and the best he could hope for was to keep the illness at bay as long as possible. The doctor sent Abel's former teacher Bernt Holmboe a certificate, reporting the young man's state of health:

. . . Shortly after his arrival at Froland Ironworks he suffered a severe attack of pneumonia with considerable expectoration of blood, which ceased after a brief period. But a chronic cough and great weakness have compelled him to rest in bed, where he must still remain; furthermore, he cannot be permitted to be exposed to the slightest variation in temperature.
   More serious, the dry cough with stinging pains in the chest makes it very probable that he suffers from hidden chest and bronchial tubercles, which easily can result in a subsequent chest phthisis, partially on account of his constitution.
   Due to this precarious state of health . . . it is most unlikely that he will be able to return to Oslo before the spring. Until then, he will be unable to discharge the duties of his office, even if the outcome of his illness should be the most desirable.

Crelle received the bad news in Berlin, and redoubled his efforts to secure Abel a position, advising the German minister that it would be good to transfer Abel to a warmer climate.

On 8 April, Crelle sent his protégé good news:

The Education Department has decided to call you to Berlin for an appointment . . . In what capacity you will be appointed and how much you will be paid I cannot tell you, for I do not know myself . . . I only wanted to hurry to let you hear the main news; you may be certain that you are in good hands. For your future you need no longer have any concern; you belong to us and are secure.

If only.

Abel was too ill to travel. He had to stay in Froland, where despite Crelly's nursing he became weaker and weaker, and his cough grew worse. He left his bed only to allow the sheets to be changed. When he tried to do some mathematics, he found he was unable to write. He began to dwell on the past, and his poverty, but he did not take his feelings out on the people he loved, remaining cooperative and good-natured to the very end.

Crelly naturally found it more and more difficult to hide her distress from her fiancé. Marie or Hanna kept her company at the bedside. Abel's worsening cough was stopping him from sleeping, and the family hired a nurse to look after him overnight so that Crelly could get some rest.

On the morning of 6 April, after a night of severe pain, Abel died. Hanna wrote, “He endured his worst agony during the night of 5 April. Toward morning he became more quiet, and in the forenoon, at 11 o'clock, he expired his last sigh. My sister and his fiancée were with him in the last moment, and saw his quiet passing into the arms of death.”

Five days later, Crelly wrote to Catharine Hansteen's sister Henriette Fridrichsen, asking her to tell Catharine the sad news. “My dearest love, yes, only duty could make me demand this, for I owe your sister, Fru Hansteen, so much. I take the pen with trembling hand to ask you to inform her that she has lost a kind, devout son who loved her so infinitely.

“My Abel is dead!. . . I have lost all on earth. Nothing, nothing have I left. Pardon me, the unfortunate can write no more. Ask her to accept the enclosed lock of my Abel's hair. That you will prepare your sister for this in the most lenient way asks your miserable C. Kemp.”

M
athematicians are never satisfied.

Whenever a problem is solved it only raises new questions. Soon after Abel's death, his proof that some quintics can't be solved by radicals started to become recognized. But Abel's work was just the start. Although all previous attempts to solve
all
quintics had ground to a halt, a few very clever mathematicians had proved that some quintics
can
be solved by radicals. Not just obvious ones, like
x
⁵
– 2 = 0, where
x
=
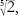but surprising ones like
x
⁵
+ 15
x
+ 12 = 0, though the solution is too complicated to state here.

This was a puzzle. If some quintics are solvable and some not, what distinguishes one kind from the other?

The answer to this question changed the course of mathematics, and mathematical physics. Even though the answer was given more than 170 years ago, it is still yielding important new discoveries. In retrospect, it is astonishing how far-reaching are the consequences of an innocent question about the internal structure of mathematics. Solving quintics, it appeared, had no practical use whatsoever. If some problem in engineering or astronomy involved a quintic, there were numerical methods to determine a solution to as many decimal places as were needed. The solvability—or not—of a quintic by radicals was a classic example of “pure” mathematics, of questions asked for reasons that interested no one but mathematicians.

How wrong you can be.

Abel had discovered an obstacle to the solution of certain quintics by radicals. He had proved that this obstacle genuinely prevented such solutions existing for at least some quintics. The next step forward, the pivot
upon which our entire story revolves, was made by someone who looked the gift horse firmly in the teeth and asked the kind of question that mathematicians cannot resist when some major problem has been solved. “Yes, that's all very nice . . . but why does it
really
work?”

The attitude may seem rather negative, but time and time again it has proved its worth. The underlying philosophy is that most mathematical problems are too difficult for anyone to solve. So when somebody manages to solve something that has baffled all predecessors, merely celebrating the great solution is not enough. Either the solver got lucky (mathematicians do not believe in that sort of luck) or some special reason made the solution possible. And if it proves possible to understand the
reason
. . . why, lots of other problems might yield to similar methods.

So while Abel was polishing off the specific question, “Can every quintic be solved?” and getting a clear “no,” an even deeper thinker was wrestling with a far more general issue: which equations can be solved by radicals, and which cannot? To be fair, Abel had begun to think along those lines, and might have found the answer if tuberculosis had spared him.