Why Beauty is Truth (9 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

3, 4, 5, 6, 8, 10, 12, 15, 16, 20.
We now know that they
cannot
be constructed when the number of sides is
7, 9, 11, 13, 14, 18, 19.
which leaves one number in this range, 17, as yet unaccounted for. The story of the 17-gon will be told in its rightful place; it is important for more reasons than purely mathematical ones.
In discussing geometry, there is no substitute for drawing on a sheet of paper with a real straightedge and real compass. It gives you a feel for how the subject fits together. I'm going to take you through my favorite construction, for the regular hexagon. I learned it from a book my uncle gave me in the late 1950s, called
Man Must Measure
, and it's lovely:
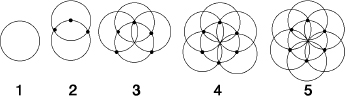
How to construct a regular hexagon.
Fix the radius of the compass throughout, so all circles will be of the same size. (1) Draw a circle. (2) Choose a point on it and draw a circle centered at that point. This crosses the original circle in two new points. (3) Draw circles with these points as centers, to get two more crossings. (4) Draw circles with
these
points as centers; both pass through the same new
crossing point. The six points can now be connected to form a regular hexagon. It is aesthetically pleasing (though mathematically unnecessary) to complete the picture with (5): Draw a circle centered on the sixth point. Then six circles meet at the center of the original one, forming a flower shape.
Euclid used a very similar method, which is simpler but not quite so pretty, and he
proved
that it works: you can find it in Proposition 15 of Book IV.
THE PERSIAN POET
W
Â
ake! For the Sun, who scattered into flight
Â
The Stars before him from the Field of Night,
Â
Drives Night along with them from Heav'n and strikes
           Â
The Sultán's Turret with a Shaft of Light.
Â
To most of us, the name of Omar Khayyám is indelibly associated with his long ironic poem, the
Rubaiyat
, and specifically with the elegant translation into English by Edward Fitzgerald. To historians of mathematics, however, Khayyám has a greater claim to fame. He was prominent among the Persian and Arab mathematicians who took up the torch that the Greeks had dropped, and continued the development of new mathematics after scholars in Western Europe descended into the dark ages and its scholars abandoned theorem-proving for theological disputation.
Among Khayyám's great achievements is the solution, by respectable methods of Greek geometry, of cubic equations. His techniques necessarily went beyond the straightedge and compass that tacitly limit Euclidean geometry, because these tools are simply not up to the jobâa fact that the Greeks strongly suspected, but could not prove because they lacked the necessary point of view, which was not geometry but algebra. But Khayyám's methods did not go
much
beyond straightedge and compass. He relied on special curves known as “conic sections” because they can be constructed by slicing a cone with a plane.

The conventional wisdom in popular science writing is that every equation halves a book's sales. If true, this is very bad news, because nobody would be able to understand some of the key themes of this book without being shown a few equations. The next chapter, for instance, is about Renaissance mathematicians' discoveries of formulas that solve any cubic or quartic equation. I can get away without showing you what the quartic formula looks like, but we really will need to take a quick look at the formula for the cubic. Otherwise, all I can tell you is something like “multiply some numbers by some other numbers and add some numbers to that, and then take the square root, then add another number and take the cube root of the result;
then
do the same thing again with slightly different numbers; finally, add the two results together. Oh, and I forgot to mentionâyou have to do some dividing as well.”
Some writers have challenged the conventional wisdom and even written books
about
equations. They seem to be following the old showbiz saying, “If you've got a wooden leg, wave it.” Now, there is a sense in which this book is about equations; but just as you can write a book about mountains without requiring your readers to climb one, you can write a book about equations without requiring your readers to solve one. Still, readers of a book about mountains probably won't understand it if they have never seen a mountain, so it really will help us both a lot if I show you a few carefully selected equations.
The ground rules, slanted heavily in your favor, are these: The word is “show.” I want to you to
see
the equation. You needn't
do
anything with it. When necessary, I will pick the equation to pieces and explain which features matter for our story. I will
never
ask you to solve an equation or calculate with one. And I will do my utmost to avoid them whenever I can.
When you get to know them, equations are actually rather friendly. They are clear, concise, sometimes even beautiful. The secret truth about equations is that they are a simple, clear language for describing certain “recipes” for calculating things. When I can tell you the recipe in words, or just give you enough feel for how it goes that the details don't matter, I will. On rare occasions, though, it becomes so cumbersome to use words that I'll have to use symbols.
There are three kinds of important symbols for this book, and I'll mention two of them now. One is our old friend
x
, “the unknown.” This symbol stands for a number that we do not yet know, but whose value we are desperately trying to find out.
The second type of symbol is little raised numbers, like
2
or
3
or
4
. They are instructions to multiply some other number by itself the appropriate number of times. So 5
3
means 5 Ã 5 Ã 5, which is 125, and
x
2
means
x
Ã
x
, where
x
is our symbol for an unknown number. They are read as “squared,” “cubed,” “raised to the fourth power,” etc., and collectively they are referred to as
powers
of the number concerned.
I haven't the foggiest idea why. They have to be called something.

Either the Babylonian method for solving quadratic equations was passed on to the ancient Greeks, or they reinvented it. Heron, who lived in Alexandria somewhere between 100 BCE and 100, discussed a typical Babylonian-style problem in Greek terminology. Around the year 100, Nichomachus, probably an Arabian hailing from Judea, wrote a book called
Introductio Arithmetica
in which he abandoned the Greek tradition of representing numbers by geometrical quantities such as lengths or areas. To Nichomachus, numbers were quantities in their own right, not lengths of lines. Nichomachus was a Pythagorean, and his work shows it: he deals only in whole numbers and their ratios, and he uses no symbols. His book became the standard arithmetic text for the next millennium.
Symbolism entered into algebra in the work of a Greek mathematician named Diophantus, sometime around 500. The only thing that we know about Diophantus is his age at death, and that comes to us via a route of dubious authenticity. A Greek collection of algebra problems contains one that reads like this: “Diophantus spent one-sixth of his life as a boy. His beard grew after a further one-twelfth. He married after another one-seventh, and his son was born five years later. The son lived to half his father's age and the father died four years after the son. How old was Diophantus when he died?”
Using that ancient algebraist's own methods, or more modern ones, you can deduce that he must have been 84. It was a good age, assuming the algebra problem is based on fact, which is questionable.
That's all we know of his life. But we know quite a bit about his books, through later copies and references in other documents. He wrote one book on polygonal numbers, and part of it survives. It is arranged in Euclidean style, proves theorems using logical arguments, and has little mathematical significance. Far more significant were the 13 books of the
Arithmetica.
Six of them are still in existence, thanks to a thirteenth-century Greek copy of
an earlier copy. Four more may have surfaced in a manuscript found in Iran, but not all scholars are convinced that it traces back to Diophantus.
The
Arithmetica
is presented as a series of problems. In the preface, Diophantus says he wrote it as a book of exercises for one of his students. He used a special symbol for the unknown, and different symbols for its square and cube that seem to be abbreviations of the words
dynamis
(power) and
kybos
(cube). The notation is not very structured. Diophantus adds symbols by putting them next to each other (as we now do for multiplication) but has a special symbol for subtraction. He even has a symbol for equality, though this may have been introduced by later copyists.
Mostly, the
Arithmetica
is about solving equations. The first surviving book discusses linear equations; the other five treat various kinds of quadratic equations, often in several unknowns, and a few special cubic equations. A key feature is that the answers are always integers or rational numbers. Today we call an equation “Diophantine” if its solutions are restricted to integers or rational numbers. A typical example from the
Arithmetica
is, “Find three numbers such that their sum, and the sum of any two, is a perfect square.” Try itâit's by no means easy. Diophantus's answer is 41, 80, and 320. The sum of all three is 441 = 21
2
. The sums of pairs are 41 + 80 = 121 = 11
2
, 41 + 320 = 361 = 19
2
, and 80 + 320 = 400 = 20
2
. Clever stuff.
Diophantine equations are central to modern number theory. A famous example is Fermat's “last theorem,” which states that two perfect cubes, or higher powers, cannot add to form a similar power. With squares, this kind of thing is easy, and goes back to Pythagoras: 3
2
+ 4
2
= 5
2
or 5
2
+ 12
2
= 13
2
. But you can't do the same with cubes, fourth powers, fifth powers, or anything higher than the square. Pierre de Fermat scribbled this conjecture (without a proof; it wasn't a theorem despite its name) in the margin of his personal copy of the
Arithmetica
around 1650. It took nearly 350 years before Andrew Wiles, a British-born number theorist living in America, proved that Fermat was right.
The historical tradition in mathematics is sometimes very long.
