Why Beauty is Truth (5 page)

This emphasis on 60 and 360 still lingers today, in our use of 360 degrees in a full circle—one degree per Babylonian day—and in the 60 seconds in a minute and 60 minutes in an hour. Old cultural conventions have incredible staying power. I find it amusing that in this age of spectacular computer graphics, moviemakers still date their creations in Roman numerals.

Nabu-Shamash would have learned all of this, except the “zero” sign, at an early stage of his education. He would have become adept at impressing thousands of tiny cuneiform wedges into damp clay at speed. And just as today's students grapple with the transition from whole numbers to fractions and decimals, Nabu-Shamash would eventually have been faced with the Babylonian method for representing numbers like one-half, or
one-third, or the more complicated subdivisions of unity dictated by the brutal realities of astronomical observations.

To avoid spending whole afternoons drawing wedges, scholars represent cuneiform numbers with a mixture of old and new. They write the decimal numbers depicted in the successive groups of wedges, using commas to separate them. So the final group in the figure would be written 1,3,12. This convention saves a lot of expensive typesetting and is easier to read, so we'll go along with the scholars.

How would a Babylonian scribe have written the number “one-half”?

In our own arithmetic, we solve this problem two different ways. We either write the number as a fraction, ½, or introduce the famous “decimal point” and write it as 0.5. The fractional notation is more intuitive and came earlier historically; decimal notation is more difficult to grasp, but it lends itself better to computation because the symbolism is a natural extension of the “place-value” rules for whole numbers. The symbol 5 in 0.5 means “5
divided by
10,” and in 0.05 it means “5 divided by 100.” Moving a symbol one place to the left multiplies it by 10; moving it one place to the right divides it by 10. All very sensible and systematic.

As a result, decimal arithmetic is just like whole-number arithmetic, except that you have to keep track of where the decimal point goes.

The Babylonians had the same idea, but in base 60. The fraction ½ should be some number of copies of the fraction 1/60. Clearly the right number is 30/60, so they wrote “one-half” as 0;30, where scholars use the semicolon to denote the “sexagesimal point,” which in cuneiform notation was again a matter of spacing. The Babylonians managed some fairly advanced calculations: for example, their value for the square root of 2 was 1;24,51,10, which differs from the true value by less than one part in a hundred thousand. They used this precision to good advantage in both theoretical mathematics and astronomy.

The most exciting technique that Nabu-Shamash would have been taught, as far as our central theme of symmetry is concerned, is the solution of quadratic equations. We know quite a lot about Babylonian methods for solving equations. Of the roughly one million Babylonian clay tablets known to exist, about five hundred deal with mathematics. In 1930, the orientalist Otto Neugebauer recognized that one of these tablets demonstrated a complete understanding of what today we call
quadratic equations. These are equations that involve an unknown quantity and its square, together with various specific numbers. Without the square, the equation would be called “linear,” and such equations are the easiest to solve. An equation that involves the cube of the unknown (multiply it by itself, then multiply that by the unknown again) is called “cubic.” The Babylonians seem to have possessed a clever method for finding approximate solutions to certain types of cubic equation, based on numerical tables. All that we are certain of, however, are the tables themselves. We can only infer what they were used for, and cubic equations are most likely. But the tablets Neugebauer studied make it plain that the Babylonian scribes had mastered the quadratic.

A typical one, which dates back about 4000 years, asks, “Find the side of a square if the area minus the side is 14,30.” This problem involves the square of the unknown (the area of the square) as well as the unknown itself. In other words, it asks the reader to solve a quadratic equation. The same tablet rather offhandedly provides the answer: “Take half of 1, which is 0;30. Multiply 0;30 by 0;30, which is 0;15. Add this to 14,30 to get 14,30;15. This is the square of 29;30. Now add 0;30 to 29;30. The result is 30, the side of the square.”

What's going on here? Let's write the steps in modern notation.

 

 

The most complicated step is the fourth, which finds a number (it is 29½) whose square is 870¼. The number 29½ is the
square root
of 870¼. Square roots are the main tool for solving quadratics, and when mathematicians tried to use similar methods to solve more complicated equations, modern algebra was born.

Later we will interpret this problem using modern algebraic notation. But it is important to realize that the Babylonians did not employ an algebraic
formula as such. Instead, they described a specific
procedure
, in the form of a typical example, that led to an answer. But they clearly knew that
exactly the same procedure would work if the numbers were changed.

In short, they knew how to solve quadratics, and their method—though not the form in which they expressed it—was the one we use today.

How did the Babylonians discover their method for solving quadratics? There is no direct evidence, but it seems likely that they came across it by thinking geometrically. Let's take an easier problem that leads to the same recipe. Suppose we find a tablet that says, “Find the side of a square if the area plus two of the sides is 24.” In more modern terms, the square of the unknown plus twice the unknown equals 24. We can represent this question as a picture:

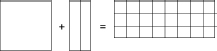
Geometric picture of a quadratic equation.

Here the vertical dimension of the square and rectangle to the left of the equal sign corresponds to the unknown, and the small squares are of unit size. If we split the tall rectangle in half and glue the two pieces onto the square, we get a shape like a square with one corner missing. The picture suggests that we should “complete the square” by adding in the missing corner (shaded square) to both sides of the equation:

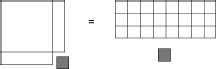
Completing the square.

Now we have a square on the left and 25 unit squares on the right. Rearrange those into a 5 × 5 square:

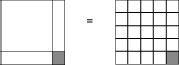
Now the solution is obvious.

Thus the unknown plus one, squared, equals five squared. Taking square roots, the unknown plus one equals five—and you don't have to be a genius to deduce that the unknown is four.

This geometric description corresponds precisely to the Babylonian method for solving quadratics. The more complicated example from the tablet uses exactly the same recipe. The tablet only states the recipe and doesn't say where it comes from, but the geometric picture fits other circumstantial evidence.

M
any of the greatest mathematicians of the ancient world lived in the Egyptian city of Alexandria, a city whose origins lie among five substantial oases to the west of the Nile, out in the Western Desert. One of them is Siwa, notable for its salt lakes, which grow during the winter and shrink in the summer heat. The salt contaminates the soil and creates major headaches for archaeologists because it is sucked up into the ancient stone and mud-brick remains and slowly destroys the fabric of the buildings.