Why Beauty is Truth (7 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Triangular and square numbers.
Pythagoreanism embraced some nutty numerologyâit considered 2 to be male and 3 female, for exampleâbut the view that the deep structure of nature is mathematical survives today as the basis of most theoretical science. Although later Greek geometry was less mystical, the Greeks generally saw mathematics as an end in itself, more a branch of philosophy than a tool.
There are reasons to believe that this does not tell the whole story. It is well established that Archimedes, who may have been a pupil of Euclid's, employed his mathematical abilities to design powerful machines and engines of war. There survive a tiny number of intricate Greek mechanisms whose cunning design and precision manufacture hint at a well-developed tradition of craftsmanshipâan ancient version of “applied mathematics.” Perhaps the best-known example is a machine found in the sea near the small island of Antikythera that appears to be a calculating device for astronomical phenomena built from a complex tangle of interlocking cogwheels.
Euclid's
Elements
certainly fits this rarefied view of Greek mathematicsâpossibly because that view is largely based on the
Elements.
The book's main emphasis is on logic and proof, and there is no hint of practical applications. The most important feature of the
Elements
, for our story, is not what it contains but what it does not.

Euclid made two great innovations. The first is the concept of proof. Euclid refuses to accept any mathematical statement as being true unless it is supported by a sequence of logical steps that deduces it from statements already known to be true. The second innovation recognizes that the proof process must start somewhere, and that these initial statements cannot be proved. So Euclid states up front five basic assumptions on which all his later deductions rest. Four of these are simple and straightforward: two points may be joined by a line; any finite line can be extended; a circle can be drawn with any center and any radius; all right angles are equal.
But the fifth postulate is very different. It is long and complicated, and what it asserts is not nearly so reasonable and obvious. Its main implication is the existence of parallel linesâstraight lines that never meet, but run forever in the same direction, always the same distance apart, like two sidewalks on either side of an infinitely long, perfectly straight road. What Euclid actually states is that whenever two lines cross a third, the first two
lines must meet on whichever side creates two angles that add up to less than two right angles. It turns out that this assumption is logically equivalent to the existence of exactly one line parallel to a given line and passing through a given point (not on the given line).
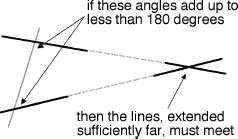
Euclid's fifth postulate.
For centuries the fifth postulate was viewed as a blemishâsomething to be removed by deducing it from the other four, or to be replaced by something simpler and just as obvious as the others. By the nineteenth century, mathematicians understood that Euclid was absolutely right to include his fifth postulate, because they could prove that it can't be deduced from his other assumptions.

To Euclid, logical proofs were an essential feature of geometry, and proof remains fundamental to the mathematical enterprise. A statement that lacks a proof is viewed with suspicion, however much circumstantial evidence seems to favor it and however important its implications may be. Physicists, engineers, and astronomers tend to view proofs with disdain, as a kind of pedantic appendage, because they have an effective substitute: observation.
For instance, imagine an astronomer trying to calculate the movements of the Moon. He will write down mathematical equations that determine the Moon's motion, and promptly get stuck because there seems to be no way to solve the equations exactly. So the astronomer may tinker with the equations, introducing various simplifying approximations. A mathematician will worry that these approximations might have a serious effect on the answer, and will want to prove that they do not cause trouble. The astronomer has a different way to check that what he has done makes sense.
He can see whether the motion of the Moon fits his calculations. If it does, that simultaneously justifies the method (because it got the right answer) and verifies the theory (for the same reason). The logic here is not circular because if the method is mathematically invalid, then it will almost certainly fail to predict the Moon's motion.
Without the luxury of observations or experiments, mathematicians have to verify their work by its internal logic. The more important the implications of some statement are, the more important it is to make sure that the statement is true. So proof becomes even more crucial when the statement is something that everyone wants to be true, or that would have enormous implications if it
were
true.
Proofs cannot rest on thin air, and they cannot trace logical antecedents back forever. They have to start somewhere, and where they start will by definition be things that have not beenâand will not beâproved. Today we call these unproved starting assumptions
axioms.
The axioms for a piece of mathematics are the rules of the game.
Anyone who objects to the axioms can change them if they wish: however, the result will be a different game. Mathematics does not assert that some statement is
true:
it asserts that if we make various assumptions, then the statement concerned must be a logical consequence. This does not imply that the axioms are unchallengeable. Mathematicians may debate whether a given axiomatic system is better than another for some purpose, or whether the system has any intrinsic merit or interest. But these discussions are not about the internal logic of any particular axiomatic game. They are about which games are worthwhile, interesting, or fun.

The consequences of Euclid's axiomsâhis long, carefully selected chains of logical deductionsâare extraordinarily far-reaching. For example, he provesâwith logic that in his day was considered impeccableâthat once you agree to his axioms you necessarily must conclude that:
â¢Â The square on the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides.
â¢Â There exist infinitely many prime numbers.
â¢Â There exist irrational numbersânot expressible as an exact fraction. An example is the square root of two.
â¢Â There are precisely five regular solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
â¢Â Any angle can be divided exactly into two equal parts using only straightedge and compass.
â¢Â Regular polygons with 3, 4, 5, 6, 8, 10, and 12 sides can be constructed exactly using only straightedge and compass.
I have expressed these “theorems,” as we call any mathematical statement that has a proof, in modern terms. Euclid's point of view was rather different: he did not work directly with numbers. Everything that we would interpret as properties of numbers is stated in terms of lengths, areas, and volumes.

The content of the
Elements
divides into two main categories. There are theorems, which tell you that something is true. And there are constructions, which tell you how to
do
something.
A typical and justly famous theorem is Proposition 47 of Book I of the
Elements
, usually known as the Pythagorean theorem. This tells us that the longest side of a right triangle bears a particular relationship to the other two sides. But it does not, without further effort or interpretation, provide a method for achieving any goal.
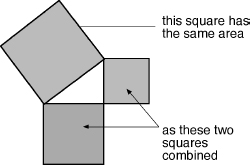
The Pythagorean theorem.
A construction that will be important in our story is Proposition 9 of Book I, where Euclid solves the “bisection problem” for angles. Euclid's
method of bisecting an angle is simple but clever, given the limited techniques available at this early stage of the development.
