Why Beauty is Truth (12 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Earlier, I mentioned two kinds of mathematical symbol, both of which we see in an expression such as
x
3
, for the cube of the unknown. The first kind of symbol is the use of letters (
x
in this case) to stand for numbersâeither unknown, or known but arbitrary. The second kind uses raised numbers to indicate powersâso the superscript
3
here indicates the cube
x
Ã
x
Ã
x.
Now we come to a third kind of symbol, the last that we will need.
This third type of symbol is very pretty, and it looks like this: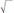 . This symbol means “square root.” For instance,
. This symbol means “square root.” For instance,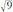 , “the square root of nine,” means the number that
, “the square root of nine,” means the number that
when multiplied by itself
gives the answer 9. Since 3 Ã 3 = 9, we see that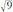 = 3. It's not always that easy, however. The most notorious square root, which according to a very unlikely legend caused the mathematician who drew attention to it, Hippasus of Metapontum, to be thrown overboard from a boat, is the square root of two,
= 3. It's not always that easy, however. The most notorious square root, which according to a very unlikely legend caused the mathematician who drew attention to it, Hippasus of Metapontum, to be thrown overboard from a boat, is the square root of two,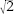 . An exact expression in decimals has to go on forever. It starts like this:
. An exact expression in decimals has to go on forever. It starts like this:
1.4142135623730950488,
but it can't
stop
there, because the square of that number is actually
1.99999999999999999999522356663907438144,
which obviously is not quite the same as 2.
This time we do know where the symbol came from. It is a distorted form of the letter “r,” standing for “radix,” the Latin for “root.” Mathematicians understand it that way and read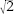 as “root two.”
as “root two.”
Cube roots, fourth roots, fifth roots, and so on are shown by putting a small raised number in front of the “root” sign, like this:
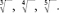
The cube root of a given number is the number that has the given number as its cube, and so on. So the cube root of 8 is 2, because 2
3
= 8. Again, the cube root of 2 can be expressed only approximately in decimal notation. It starts out like this:
1.2599210498948731648
and continues, if you have sufficient patience, forever.
It is this number that turns up in the ancient problem of doubling the cube.

By the year 400, Greek mathematics was no longer on the cutting edge. The action moved east, to Arabia, India, and China. Europe descended into the “Dark Ages,” and while these were not quite as dark as they have often been painted, they were dark enough. The spread of Christianity had the unfortunate side effect of concentrating learning and scholarship in the churches and monasteries. Many monks copied the works of mathematical greats like Euclid, but very few of them understood what they were copying. The Greeks could dig a tunnel through a mountain from both ends and make it meet in the middle; the early Anglo-Saxon method of surveying was to lay out a design,
full scale
, in a field. Even the notion of drawing to scale had been lost. If the Anglo-Saxons had wanted to make an accurate map of England, they would have made it the same
size
as England. They did make maps of conventional size, but not very accurate ones.
By the end of the fifteenth century, the focus of mathematical activity was once again swinging back to Europe. As the Middle and Far East ran out of creative steam, Europe was getting its second wind, struggling free of the embrace of the Church of Rome and its fear of anything new. Ironically, the new center of intellectual activity was Italy, as Rome lost its grip on its own backyard.
This sea change in European science and mathematics began with the publication, in 1202, of a book called the
Liber Abbaci
, written by Leonardo of Pisa, who much later was given the nickname Fibonacciâson of Bonaccioâand is now known by that name even though it was invented in the nineteenth century. Leonardo's father, Guilielmo, was a customs officer in Bugia, now Algeria, and in his work must have come across people from many cultures. He taught his son the newfangled numerical symbols invented by the Hindus and the Arabs, the forerunners of our decimal digits 0 through 9. Leonardo later wrote that he “enjoyed so much the instruction that I continued to study mathematics while on business trips to Egypt, Syria, Greece, Sicily, and Provence, and there enjoyed disputations with the scholars of those places.”
At first sight, the title of Leonardo's book seems to indicate that it is about the abacus, a mechanical calculating device using beads that slide on wires, or pebbles in a groove in the sand. But just as the Latin word calculus, referring to one of those small pebbles, later acquired a different and more technical meaning, so the word abbaco, the counting frame, came to mean the art of computation. The
Liber Abbaci
was the first arithmetic text to bring the Hindu-Arabic symbols and methods to Europe. A large part of it is given over to the new arithmetic's applications to practical subjects like currency exchange.
One problem, about an idealized model of the growth of a population of rabbits, led to the remarkable sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on, where each number from 2 onward is the sum of the preceding two numbers. This “Fibonacci sequence” is Leonardo's greatest claim to fameânot for its rabbit-breeding implications, which are nil, but for its remarkable mathematical patterns and its key role in the theory of irrational numbers. Leonardo could have had no idea that this little
jeu d'esprit
would come to eclipse the entire rest of his life's work.
Leonardo wrote several other books, and his
Practica Geometriae
of 1220 contained a large part of Euclid, plus some Greek trigonometry. Book X of Euclid's
Elements
discusses irrational numbers composed of nested square roots, of the type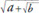 . Leonardo proved that these irrationals are inadequate for solving cubic equations. This does not imply that the roots of the cubic cannot be constructed by ruler and compass, because other combinations of square roots might yield solutions. But it was the first hint that cubics might not be solvable using only Euclid's tools.
. Leonardo proved that these irrationals are inadequate for solving cubic equations. This does not imply that the roots of the cubic cannot be constructed by ruler and compass, because other combinations of square roots might yield solutions. But it was the first hint that cubics might not be solvable using only Euclid's tools.
In 1494, Luca Pacioli pulled together much existing mathematical knowledge in a book on arithmetic, geometry, and proportion. It included the Hindu-Arabic numerals, commercial mathematics, a summary of Euclid, and Ptolemy's trigonometry. A running theme was the element of design in nature, embodied in proportionsâthe human body, perspective in art, the theory of color.
