Why Beauty is Truth (29 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

On the other hand, satisfies the cubic equation
satisfies the cubic equation
x
3
â 2 = 0, and this is its minimum polynomial. The degree is 3, which is not a power of 2. Therefore the assumption that the cube can be duplicated using straightedge and compass leads, by impeccable logic, to the conclusion that 3 is a power of 2. This is obviously not true. By
reductio ad absurdum
, therefore, no such construction can exist.

Trisection of the angle is impossible for a similar reason, but the proof is slightly more involved.
First,
some
angles can be trisected exactly. A good example is 180°, which trisects to 60°, an angle that we can construct by making a regular hexagon. So the impossibility proof begins by picking some other angle and proving that this choice cannot be trisected. The simplest angle to pick is 60° itself. One-third of that is 20°, and we will show that 20° cannot be constructed using straightedge and compass.
This is a sobering thought. Look at a protractor, an instrument for measuring angles. Confidently marked on it are angles of 10°, 20°, and so on. But those angles are not exactâfor a start, the inked lines have thickness. We can make an angle of 20° that's good enough for an architectural or engineering drawing. But we can't construct a perfect 20° angle using Euclidean methodsâthat's what we plan to prove.
The key to this puzzle is trigonometry, the quantitative study of angles. Suppose that we start with a hexagon inscribed in a circle of radius 1. Then we can find a 60° angle, and if we could trisect it, we could construct the bold line in the figure (next page).
Suppose this line has length
x.
Trigonometry informs us that
x
satisfies the equation 8
x
3
â 6
x
â 1 = 0. As in the problem of duplicating the cube, this is cubic, and again it is the minimum polynomial of
x.
But if
x
is constructible then the degree of its minimum polynomial must be a power of
2. Same contradiction, same conclusion: the proposed construction is impossible.

Trisecting an angle of 60° is equivalent to constructing the length marked
x.
The way I have presented these proofs conceals a deeper structure, and from a more abstract perspective Wantzel's solutions of these two problems of antiquity both boil down to symmetry arguments: the Galois groups of the equations that correspond to the geometry have the wrong structure for straightedge-and-compass constructions. Wantzel was well aware of Galois groups, and in 1845 he developed a new proof that some algebraic equations cannot be solved by radicals. The proof followed Ruffini and Abel closely, but simplified and clarified the ideas. In the introduction Wantzel states,
Although [Abel's] proof is finally correct, it is presented in a form too complicated and so vague that it is not generally accepted. Many years previous, Ruffini . . . had treated the same question in a manner much vaguer still . . . In meditating on the researches of these two mathematicians . . . we have arrived at a form of proof which appears so strict as to remove all doubt on this important part of the theory of equations.

The sole remaining problem of antiquity was squaring the circle, a task that amounts to constructing a line of length
exactly
equal to Ï. Proving this construction impossible turned out to be much more difficult. Why? Because instead of Ï having a minimum polynomial of the wrong degree, it turned out to have no minimum polynomial
at all.
There is no polynomial equation with rational coefficients having a root equal to Ï. You can come as close as you like, but you can never get exactly Ï.
The mathematicians of the nineteenth century realized that the distinction between rational and irrational numbers could profitably be refined. There were different kinds of irrational. Relatively “tame” irrationals like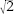 could not be represented as exact fractions, that is, as rational numbers, but they could be represented
could not be represented as exact fractions, that is, as rational numbers, but they could be represented
in terms of
rational numbers. They satisfied equations whose coefficients were rational numbersâin this case,
x
2
â 2 = 0. Such numbers were said to be “algebraic.”
But mathematicians realized that in principle there might exist irrational numbers that were
not
algebraic and whose link to the rationals was far more indirect than that for the algebraic numbers. They
transcended
the rational realm altogether.
The first question was, do such “transcendental” numbers actually exist? The Greeks supposed that all numbers might be rational until Hippasus disillusioned them, and Pythagoras allegedly was so incensed that he drowned the messenger. (More likely, Hippasus was just expelled from the Pythagorean cult.) The mathematicians of the nineteenth century were aware that any belief that all numbers are algebraic was equally likely to lead to tragedy, but for many years they lacked a Hippasus. All they had to do was to prove that some specific real numberâÏ was a plausible candidateâis not algebraic. But it's difficult enough to prove that some number, Ï, for example, is irrational, and for that all you have to show is the nonexistence of any pair of integers such that one divided by the other gives you Ï. To prove that a number is not algebraic, you have to replace these hypothetical integers by all possible equations, of any degree whatsoever, and then derive a contradiction. It gets messy.
The first significant progress was made by the German mathematician and astronomer Johann Lambert in 1768. In a paper on transcendental numbers, he proved that Ï is irrational, and his method paved the way to everything that followed. It made essential use of ideas from calculus, notably the concept of an “integral.” (The integral of any given function is a function whose rate of change yields the original function.) Starting from the assumption that Ï is equal to some exact fraction, Lambert proposed to calculate a fairly complicated integral that he had invented for just this purpose, which involved not just polynomials but trigonometric functions. There are two distinct ways to calculate this integral. One of them gives the answer zero. The other proves that the answer is
not
zero.
If Ï were not a fraction, then neither method would apply, so no problems would arise. But if Ï were a fraction, zero would have to be different from itself. No way.
The details of Lambert's proof are technical, but how it works is very informative. To get started, he had to relate Ï to something simpler, and trigonometry came to his rescue. The next problem was to fix things up so that something special would happen if Ï were rational. This was where the polynomial bit came in, along with the clever idea of forming an integral. After that, the proof was a matter of comparing two distinct methods for computing the integral, and showing that they gave different answers. That bit was messy and technical, but routine for experts.
Lambert's proof was a major step forward, but plenty of irrational numbers can be constructed, the most obvious being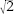 , the diagonal of a unit square. So proving Ï irrational did not prove that it was unconstructible. It meant there was no longer any point in trying to find an exact fraction for Ï, but that was a different issue altogether.
, the diagonal of a unit square. So proving Ï irrational did not prove that it was unconstructible. It meant there was no longer any point in trying to find an exact fraction for Ï, but that was a different issue altogether.

