Why Beauty is Truth (32 page)

Hamilton's great contribution to optics was unification. He took a huge variety of known results and reduced them all to the same fundamental technique. In place of a system of light rays he introduced a single quantity, the “characteristic function” of the system. Any optical configuration was thereby represented by a single equation. Furthermore, this equation
could be solved by a uniform method, leading to a complete depiction of the system of rays and its behavior. The method rested on a single fundamental principle: that light rays traveling through any system of mirrors, prisms, and lenses will follow the path that gets the light to its destination in the shortest time.

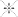
Fermat had already found some special cases of this principle, calling it the Principle of Least Time. The easiest example to explain it is light reflecting from a flat mirror. The left-hand figure below shows a light ray emerging from one point and bouncing off the mirror to reach a second point. One of the great early discoveries in optics was the law of reflection, which states that the two segments of the light ray make equal angles with the mirror.

Fermat came up with a neat trick: reflect the second segment of the ray, and the second point, in the mirror, as in the right-hand figure. Thanks to Euclid, the “equal angles” condition is the same as the statement that in this reflected representation, the path from the first point to the second is straight. But Euclid famously proved that a straight line is the shortest path between two points. Since the speed of light in air is constant, shortest
distance
equates to shortest
time.
“Unreflecting” the geometry to get back to the left-hand figure, the same statement holds. So the equal-angles condition is logically equivalent to the light ray taking the shortest time to get from the first point to the second, subject to its hitting the mirror along the way.

How the principle of least time leads to the law of reflection.

A related principle, Snell's law of refraction, tells us how light rays bend when passing from air into water, or from any medium to any other. It can be derived by a similar method, bearing in mind that light travels more slowly in water than it does in air. Hamilton went further, declaring that the same principle of minimizing time applied to all optical systems, and
capturing that thought in a single mathematical object, the characteristic function.

The mathematics was impressive, but in Hamilton's hands it led to immediate experimental payoff. Hamilton noticed that his method implied the existence of “conical refraction,” in which a single light ray hitting a suitable crystal would emerge as an entire cone of rays. In 1832 this prediction, which was a big surprise to everyone who worked in optics, was dramatically confirmed by Humphry Lloyd using a crystal of the mineral aragonite. Overnight, Hamilton became a household name in science.

By 1830, Hamilton was thinking about settling down and considered marrying Ellen de Vere, telling Wordsworth he “admired her mind.” Again he resorted to sending her poems, and was just getting ready to propose when she told him she could never leave her home village of Curragh. He interpreted this as a tactful brush-off, and he may have been right, because a year later she married someone else and moved away.

Eventually, he married Helen Bayly, a local lass who lived near the observatory. Hamilton described her as “not at all brilliant.” The honeymoon was a disaster; Hamilton worked on optics and Helen was ill. In 1834 they had a son, William Edwin. Then Helen went away for most of a year. A second son, Archibald Henry, followed in 1835, but the marriage was falling apart.

Posterity holds Hamilton's mechanico-optical analogy to have been his greatest discovery. But in his own mind, right up to his death and with increasing obsession, that honor was reserved for something very different: quaternions.

Quaternions are an algebraic structure, a close relative of complex numbers. Hamilton was convinced they held the key to the deepest regions of physics; indeed, in his final years he believed they held the key to virtually everything. History seemed to disagree, and over the next century quaternions slowly faded from public view, becoming an obscure backwater of abstract algebra with few important applications.

Very recently, however, quaternions have enjoyed a revival. While they may never measure up to Hamilton's hopes, they are increasingly recognized as an important source of significant mathematical structures. Quaternions, it turns out, are very special beasts, and they are special in just the way modern theories of physics require.

When first discovered, quaternions started a major revolution in algebra. They broke one of the important algebraic rules. Within twenty years, virtually all of the rules of algebra were routinely being broken, often bringing huge benefits, equally often leading to sterile dead ends. What the mathematicians of the mid-1850s had considered inviolable rules turned out to be merely convenient assumptions that made life simpler for algebraists but did not always match the deeper needs of mathematics itself.

In the brave new post-Galois world, algebra was no longer just about using symbols for numbers in equations. It was about the deep structure of equations—not numbers but processes, transformations, symmetries. These radical innovations changed the face of mathematics. They made it more abstract, but also more general and more powerful. And the whole area had a weird, often baffling beauty.

Until the Renaissance mathematicians of Bologna started wondering whether minus one could have a sensible square root, all of the numbers appearing in mathematics belonged to a single system. Even today, as a legacy of historical confusion about the relation of mathematics to reality, this system is known as the
real numbers.
The name is unfortunate, because it suggests that these numbers somehow belong to the fabric of the universe rather than being generated by human attempts to understand it. They are not. They are no more real than the other “number systems” invented by human imagination over the past 150 years. They do, however, bear a more direct relation to reality than most new systems. They correspond very closely to an idealized form of measurement.

A real number, essentially, is a decimal. Not as regards that specific type of notation, which is merely a convenient way to write real numbers in a form suitable for calculations, but as regards the deeper properties that decimals possess. The real numbers were born from simpler, less ambitious ancestors. First, humanity stumbled its way towards the system of “natural numbers,” 0, 1, 2, 3, 4, and so on. I say “stumbled” because in the early stages, several of these numbers were not recognized as numbers at all. There was a time when ancient Greeks refused to consider 2 a number; it was too small to be typical of “numerosity.” Numbers began at 3. Eventually, they allowed that 2 was as much a number as 3, 4, or 5, but then they balked at 1. After all, if someone claimed to have “a number of cows,” and then you found that he owned just
one
cow, he was guilty of wild exaggeration. “Number” surely meant “plurality,” which ruled out the singular.

But as notational systems developed, it became blindingly obvious that 1 was just as much a part of the computational system as its larger brethren. So it became a number—but a special, very small one. In some ways it was the most important number of all, because that's where numbers started. Adding lots of 1's together got you everything else—and for a time the notation did literally that, so that “seven” would be written as seven strokes, | | | | | | |.

Much later, Indian mathematicians recognized that there was an even more important number that
preceded
1. That wasn't where numbers started, after all. They started at zero—now symbolized by 0. Later still, it turned out to be useful to throw negative numbers into the mix—numbers
less than nothing.
So the negative whole numbers joined the system, and humanity invented the integers: . . ., –3, –2, –1, 0, 1, 2, 3,. . . But it didn't stop there.

The problem with whole numbers is that they fail to represent many useful quantities. A farmer trading grain, for instance, might wish to specify a quantity of wheat somewhere between 1 sack and 2 sacks. If it seemed about midway between, then it constituted 1½ sacks. Maybe it was a bit less, 1⅓, or a bit more, 1⅔. And so fractions were invented, with a variety of notations. Fractions interpolated between the whole numbers. Sufficiently complicated fractions interpolated exceedingly finely, as we have already seen with Babylonian arithmetic. Surely any quantity could be represented by a fraction.

Enter Pythagoras and his eponymous theorem. An immediate consequence is that the length of the diagonal of a unit square is a number whose square is exactly 2. That is to say, the diagonal has length equal to the square root of 2. Such a number must exist, because you can draw a square and it obviously
has
a diagonal, and the diagonal must have length. But as Hippasus realized to his sorrow, whatever the square root of 2 might be, it cannot be an exact fraction. It is irrational. So even more numbers were needed to fill invisible gaps in the system of fractions.

Eventually, this process seemed to halt. The Greeks abandoned numerical schemes in favor of geometry, but in 1585, a Flemish mathematician and engineer named Simon Stevin, who lived in the town of Bruges, was appointed by William the Silent to tutor his son Maurice of Nassau. Stevin rose to become inspector of the dikes, quartermaster-general of the army, and minister of finance. These appointments, especially the last two, impressed
on him the need for proper bookkeeping, and he borrowed the clerical systems of the Italians. Seeking a way of representing fractions that had the flexibility of Hindu-Arabic place notation and the fine precision of Babylonian sexagesimals, Stevin came up with a base-ten analogue of the Babylonian base-60 system: decimals.