Why Beauty is Truth (43 page)

“Relativity” is a very bad name. It's misleading because the most significant feature of Einstein's theory is that some things are
not
relative. Specifically, the speed of light is absolute. If you shine a beam of light past an observer standing in a field, and another one standing in a moving train, both will measure the
same
speed.

This is distinctly counterintuitive, and at first sight it seems absurd. The speed of light is roughly 186,000 miles per second. Clearly this is what the observer in the field should measure. What about the person on the train?

Suppose the train is traveling at 50 mph. First, imagine that there is a second train on a parallel line, also traveling at 50 mph. You look out of the window and watch it go past. How fast does it seem to you to be moving?

If it is traveling in the same direction that you are, then the answer is 0 mph. The second train will keep pace with yours, it will stay alongside it, and seem not to be moving relative to your train. If it is traveling the opposite way, then it will appear to flash past at 100 mph, because your train's 50 mph is in effect added to the speed of the oncoming train.

If you do the measurements with trains, that is what you find.

Now replace the second train by a beam of light. The speed of light, converted to the appropriate units, is 670,616,629 miles per hour. If your train were moving away from the source of the light, you would expect to observe a speed of 670,616,629 - 50 = 670,616,579 mph, because the light would have to “catch up” with the train. On the other hand, if your train were moving toward the source of the light, then you would expect the speed of light relative to the train to be 670,616,629 + 50 = 670,616,679 mph, because the movement of the train would add to the apparent speed.

According to Einstein, both of those numbers are wrong. What you will observe, in either case, is light traveling at 670,616,629 mph—exactly the same speed that the woman in the field observes.

This sounds mad. If the Newtonian rules for relative motion work for another train, why don't they work for light? Einstein's answer is that laws of physics are different from Newton's for objects that move very fast.

More precisely, the laws of physics are different from Newton's, period. But the difference only becomes apparent when objects are moving at speeds very close to the speed of light. At low speeds like 50 mph, Newton's laws are such a good
approximation
to Einstein's proposed replacements that you cannot notice any difference. But as speeds increase, discrepancies become large enough to be observed.

The basic physical point is that the symmetries of the Maxwell equations not only preserve the
equations
; they preserve the speed of light. Indeed, the speed of light is built into the equations. So the speed of light must be absolute.

It is ironic that this proposal should be called “relativity.” Einstein actually wanted to name it “Invariantentheorie”:
invariant
theory. But the name “relativity” stuck, and in any case there already existed an area of mathematics called invariant theory, so Einstein's preferred name might have been confusing. Though not half as confusing as using “relativity” to describe the invariance of the speed of light in all inertial frames.

The consequences of “relativity” are bizarre. The speed of light is a limiting speed. You can't travel faster than light, and you can't send messages faster than light. No
Star Wars
hyperdrives. Near the speed of light, lengths shrink, time slows to a crawl, and mass increases without limit. But—and here's the wonderful thing—you don't notice, because your measuring instruments
also
shrink, slow down (in the sense that time passes more slowly), or get heavier. This is why the observer in the field and the one on the train measure your light at the same speed despite their relative motion: the changes in length and time compensate exactly for the expected effects of the relative movement. This is why Michelson and Morley could not detect the Earth's motion relative to the aether.

When you are moving, everything looks the same to you as it did when you weren't moving. The laws of physics cannot tell you whether you are moving or stationary. They can tell you whether you are accelerating, but not how fast you are going if your speed is constant.

It may still seem weird, but experiments confirm the theory in exquisite detail. Another consequence is Einstein's famous formula
E
=
mc
²
, linking mass to energy, which indirectly led to the atomic bomb, though its role there is often exaggerated.

Light is so familiar to us that we seldom think about how weird it is. It seems to weigh nothing, it penetrates everywhere, and its enables us to see. What is light? Electromagnetic waves. Waves in what? The space-time continuum, which is a fancy way of saying, “we don't know.” Early in the twentieth century, the medium for the waves was thought to be the luminiferous aether. After Einstein, we understood one thing about that aether: it doesn't exist. The waves are not
in
anything.

Quantum mechanics, as we will see, went further. Not only are light waves not
in
anything: all things
are
waves. In place of a medium to support the waves—a fabric of space-time that ripples as the waves pass—the fabric
itself
is made of waves.

Einstein was not the only person to notice that the symmetries of space-time, as revealed in Maxwell's equations, are not the obvious Newtonian symmetries. In a Newtonian view, space and time are separate and different. Symmetries of the laws of physics are combinations of rigid motions of space and an independent shift in time. But as I mentioned, these transformations do not leave Maxwell's equations invariant.

Pondering this, the mathematicians Henri Poincaré and Hermann Minkowski were led to a new view of the symmetries of space and time, on a purely mathematical level. If they had described these symmetries in physical terms, they would have beaten Einstein to relativity, but they avoided physical speculations. They did understand that symmetries of the laws of electromagnetism do not affect space and time independently but mix them up. The mathematical scheme describing these intertwined changes is known as the Lorentz group, after the physicist Hendrik Lorentz.

Minkowski and Poincaré viewed the Lorentz group as an abstract expression of certain features of the laws of physics, and descriptions like “time passing more slowly” or “objects shrinking as they speed up” were thought of as vague analogies rather than anything real. But Einstein insisted that these transformations have a genuine physical meaning. Objects, and time, really do behave like that. He was led to formulate a physical theory, special relativity, that incorporated the mathematical scheme of the Lorentz group into a physical description not of space and a separate time, but of a unified space-time.

Minkowski came up with a geometric picture for this non-Newtonian physics, now called Minkowski space-time. It represents space and time as independent coordinates, and a moving particle traces out a curve—which Einstein called its
world line
—as time passes. Because no particle can travel faster than light, the slope of the world line can never get more than 45° away from the time direction. The particle's past and future always lie inside a double cone, its light cone.

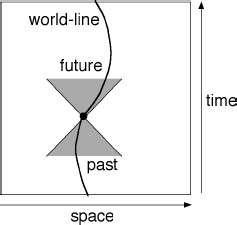
Geometry of Minkowski space-time.

That took care of electricity and magnetism, two basic forces of nature. But one basic force was still missing from this description:
gravity.
Attempting to develop a more general theory that included gravity, and again relying on the principle that the laws of nature must be symmetric, Einstein was led to general relativity: the idea that space-time itself is curved and that its curvature corresponds to mass. From these ideas emerged our current cosmology of the Big Bang, in which the universe grew from a tiny speck some 13 billion years ago, and the remarkable concept of a black hole, an object so massive that light cannot escape its gravitational field.

General relativity traces back to early work on non-Euclidean geometry, which led Gauss to the idea of a “metric,” a formula for the distance between any two points. New geometries arise when this formula is not the classic Euclidean one derived from the Pythagorean theorem. As long as the formula obeys a few simple rules, it defines a meaningful concept of “distance.” The main rule is that the distance from one point A to another C cannot decrease if you pass through a point B in between. That is, the direct distance from A to C is less than or equal to the distance from A to B plus that from B to C. This is the “triangle inequality,” so called because in Euclidean geometry it states that any side of a triangle is shorter than the other two put together.

The Pythagorean formula holds in Euclidean geometry, in which space is “flat.” So when the metric is different from the Euclidean one, we can
attribute that difference to some kind of “curvature” of space. You can visualize this as a bending of space, but that's not really the best picture because there must then be a bigger space for the original one to bend
in.
A better way to think of “curvature” is that regions of space are either compressed or stretched, so that from the inside they seem to hold less, or more, space than they do from outside. (Fans of the British TV series
Doctor Who
will be reminded of the Tardis, a spaceship/time-machine whose inside is larger than its outside.) Gauss's brilliant student Riemann extended the idea of a metric from two dimensions to any number, and he modified the idea so that distances can be defined locally—just for points that are very close together. Such a geometry is called a Riemannian manifold, and it is the most general kind of “curved space.”